混凝土强化参数的物理意义解析

由第3章分析可知，惯性力是产生混凝土率效应的重要因素。混凝土材料在受动力作用时，惯性力产生了使某质点从应力状态到应变状态转换的滞后作用，从而使该点处的损伤滞后。除了惯性力外，阻尼力、水的黏性、微裂缝的内部摩擦力以及人们尚未认识到的其他因素也会产生这种滞后效应，并且产生这种滞后效应的因素在不同的应变率和损伤水平下所产生的作用的性质不同。一般认为在高应变率下惯性力对应率效应起主要作用，在低应变率水平下黏性起主要作用。在8.4节动力学方程中包含惯性力项、阻尼项，而同时考虑了应变率对混凝土材料强度和弹性模量的强化作用，因此对在8.2节给出的混凝土材料动态强度和弹性模量与应变率的关系式中参数取值及其物理意义有待进一步探讨。值得注意的是上述动力学方程中采用的结构阻尼比为常量，并没有考虑混凝土试件在损伤过程中微裂缝的内摩擦，也没有考虑混凝土材料中的毛细水、孔隙水以及材料黏性所产生的黏性效应。

下面将以2.3节中三级配混凝土试件三分点弯拉试验结果（陈厚群，2004）为基础，并利用本章所建立的动力学方程对其数值模拟，讨论动力学方程中的惯性力项、阻尼项，以及强化参数取值对计算结果的影响，分析强化参数的物理意义。

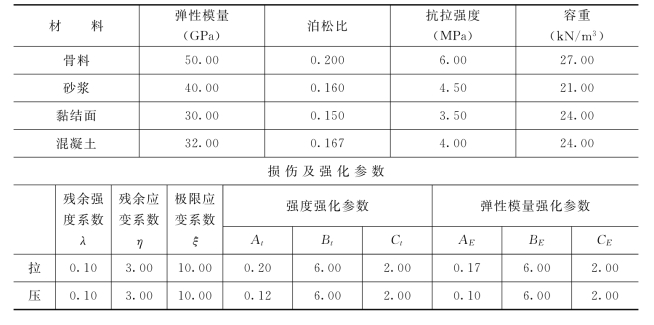
混凝土及其各相组分材料力学特性参数取值见表8.1，考虑到拉、压应变率敏感性差异，压应变率强化系数取值稍小于拉应变率强化系数，静态加载步长为0.6k N，冲击加载为600k N/s，时间步长取0.001s，计算模型如图8.5所示。依次对纯动载和施加20%、40%、60%和80%预静载后再加动载进行数值试验。数值试验主要考察引入式（8.1）和式（8.2）的强化系数，以及阻尼和惯性力对数值计算结果的影响。为此在动力加载过程中，分别按照以下三种方案进行。

表8.1　混凝土各相组分材料力学特性参数

（1）考虑阻尼，阻尼比取0.02；按表8.1给出的强化系数并按式（8.1）和式（8.2）计算动抗拉强度、动弹性模量。计算得到应力—位移曲线如图8.6（a）所示，预静载对混凝土动态增强系数的影响在图8.6（b）中给出，在图8.6（b）中同时给出了试验得到的动态增强系数随预静载水平的变化曲线，可以看出计算值和试验值吻合较好。

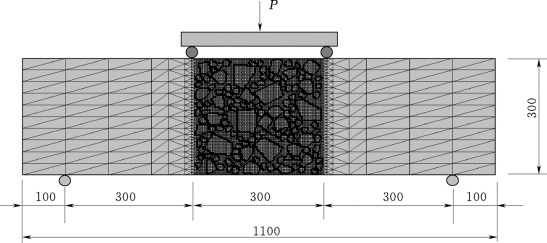
图8.5　三级配混凝土试件有限元网格剖分（单位：mm）

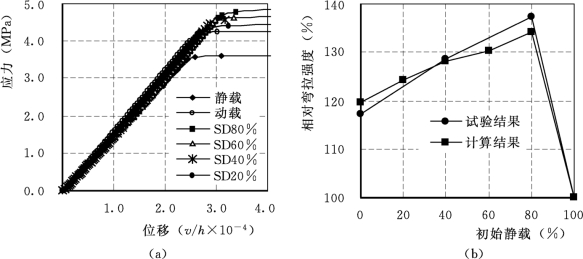
图8.6　考虑阻尼、惯性力并引入强化参数(www.xing528.com)

（a）应力—位移曲线；（b）预静载对动态增强系数的影响

（2）仅考虑阻尼，阻尼比取0.02；不引入式（8.1）和式（8.2）的强化系数，计算结果如图8.7所示。

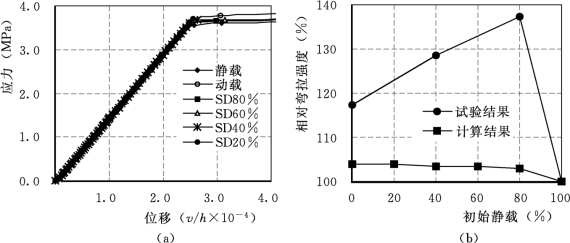
图8.7　考虑阻尼和惯性力不引入强化参数

（3）既不考虑阻尼，也不引入式（8.1）和式（8.2）的强化系数，得到如图8.8所示的计算结果。

在应力—位移曲线中，取混凝土试件下边缘中点的名义应力（σ＝PL/bh2，P为荷载，L支座间距，b为试件厚度，h为试件高度）与试件上边缘中点竖向位移（v/h）相对应。弯拉强度为应力—位移失稳时的极限名义应力。在以后章节所出现的应力—位移曲线中位移也为此含义。图例中SD#%表示加静载后再施加动载，比如SD80%表示施加80%的预静载再加动载。

从以上三种方案的计算结果看，数值模型中引入的瑞利结构阻尼几乎对计算结果不产生影响，而惯性力所产生的动态增强系数仅为1.04。显然，在不计入强化参数时，数值模拟显示几乎没有动载强化现象，更没有出现预静载对动抗弯强度的强化效应。从试验结果判断除惯性力和阻尼力之外肯定还有其他因素产生率强化作用，比如，毛细水或自由水的Stefan效应，混凝土材料本身的热活化和声子阻尼作用等因素。这些因素所产生的混凝土率效应在应变率与动态弹性模量和动态强度的关系中即式（8.1）和式（8.2）反映出来。强化参数Ht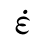（）和HE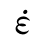（）曲线可通过具体材料的简单动态加载试验的观测结果拟合得到，可忽略具体影响因素的细节。

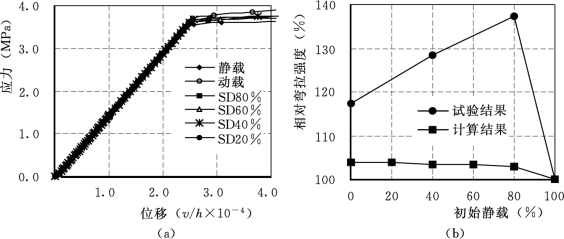
图8.8　考虑惯性力不引入强化参数并不计阻尼