【摘要】:首先要进行静载计算,并认为=(t=0)施加动载的前一时刻(t=0)的静位移在以后的动加载过程中保持不变。这里特别要注意预静载所产生的位移(或应变)不变,由于进一步加载所产生的材料弱化,静位移在上一荷载步所承担的静应力会有一部分发生转移,即在进一步加载过程中发生变化,故标识与时间有关。
8.6.2.1 有预静载的动力学增量方程
对系统施加一定的静载后,再施加动载。首先要进行静载计算,并认为 =
= (t=0)施加动载的前一时刻(t=0)的静位移在以后的动加载过程中保持不变。总位移为
(t=0)施加动载的前一时刻(t=0)的静位移在以后的动加载过程中保持不变。总位移为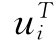 =
= (t=0)+ui,并且按总位移计算损伤参数。类似于静力学推导。
(t=0)+ui,并且按总位移计算损伤参数。类似于静力学推导。
(1)在V域内。
式中:ρ为质量密度;μ为阻尼系数; i和
i和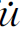 i分别为对动位移ui的二阶导数和一阶导数,即分别表示i方向的加速度和速度。这里特别要注意预静载所产生的位移(或应变)不变,由于进一步加载所产生的材料弱化,静位移在上一荷载步所承担的静应力会有一部分发生转移,即
i分别为对动位移ui的二阶导数和一阶导数,即分别表示i方向的加速度和速度。这里特别要注意预静载所产生的位移(或应变)不变,由于进一步加载所产生的材料弱化,静位移在上一荷载步所承担的静应力会有一部分发生转移,即![]() 在进一步加载过程中发生变化,故标识与时间有关。
在进一步加载过程中发生变化,故标识与时间有关。
有关变量在t+Δt时刻和t时刻的增量关系表示为
(2)应力、位移边界条件以及物理方程同式(8.24)、式(8.25)和式(8.26)。但是式(8.26)的弹性矩阵还与强化参数HE( )有关,可表示为
)有关,可表示为
8.6.2.2 有限元增量方程弱解形式
按照Galerkin方法,由动力学方程式(8.36)和应力边界条件式(8.24)得到在t+Δt时刻积分弱解形式为
由分部积分公式![]()
将式(8.38)中 变形得到(https://www.xing528.com)
变形得到(https://www.xing528.com)
由于σijδΔui,j=σijδΔεij,所以有
将上式代入式(8.38),得
同理得到在t时刻的虚功方程为
式(8.39)减去式(8.40)得
由物理方程推出
将以上三个式子代入式(8.41),得
在迭代过程中![]() 为
为 ,上式写成
,上式写成
其中 
损伤参数增量为
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




