混凝土细观损伤演化模型优化

混凝土材料中的微缺陷演化时材料会产生不同程度的劣化，因此用以描述材料损伤的宏观损伤变量必定与材料中的微（细）观缺陷存在某种关系。但是要实现这种微（细）观和宏观的联系是相当困难的，目前还没有很好的途径。在已有的损伤模型中大都以有效应力的概念来实现这种联系。

混凝土内部缺陷（微裂缝）引起的损伤，可从宏观上作如下的定性解释：在开始加载阶段，微裂缝处于均匀分布状态。在每一独立裂缝周围有一应力释放区，即损伤区。有势的裂缝区在应力释放区边缘上。继续加载，应力释放区增大，独立裂缝开始连通，直到最后形成宏观裂缝，造成局部破坏。

混凝土试件在单向拉伸时，试件的裂缝与加载方向垂直，往往沿一条主要裂缝拉断破坏，即沿最大拉伸变形方向拉断破坏；单向压缩时，试件的破裂呈现出平行的多条裂缝，即沿加载方向开裂，这主要是由于受压时自由面向外膨胀产生拉伸变形，由此可以认为混凝土的受力变形与损伤破裂主要是拉伸变形起控制作用。

由于混凝土在拉伸和压缩应力状态时微裂缝发展特性存在差异，所以损伤变量也应不同。应力状态可分解为球应力和偏应力张量两部分表达。在混凝土发生拉裂型破坏时，球应力分量为正值，与偏应力分量一起引起微裂纹的扩展。反之，在混凝土发生剪压及压碎型破坏时，球应力分量为负值，使微裂纹趋于闭合，不发生损伤。损伤主要由偏应力引起。关键是合理选择损伤演化规律，并由试验确定其参数值。

混凝土是一种准脆性材料，承载后，应力—应变曲线在宏观上呈现的非线性源于微裂纹的萌生和扩展，而不是由塑性变形引起的。由于混凝土内部损伤，实际能承担荷载的未受损伤的等效阻力体积定义为Vn，应力释放区（损伤区）的体积为Vd，总体积（或名义体积）为V。显然，在加载过程中，损伤区Vd增加，而Vn减少。假设Vn部分服从线弹性本构关系，相应的应力称为有效应力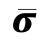ij。

采用各向同性弹性损伤力学的本构关系来描述混凝土材料的力学性质。引入标量损伤变量d＝Vd/V（0≤d≤1），再由V＝Vd+Vn可得1－d＝Vn/V，从而有效应力可定义为

＝σij/（1－d）

即

式中：σij为名义应力（柯西应力）。(www.xing528.com)

按照勒梅特应变等价原理，受损材料的名义应力σ可通过其有效应力在无损材料中的应变ε表示，若不考虑损伤对泊松比的影响，即

式中：E0为初始弹性模量；E为损伤后的弹性模量。

认为当单元的最大拉应力σmax达到其给定的极限值ft时，该单元开始发生拉伸损伤，在单向拉伸状态下，损伤变量遵循如图8.2所示的双折线演化规律，图中ft为混凝土材料的抗拉强度；ftr为破坏单元的抗拉残余强度，ftr＝λft（0＜λ≤1）（马怀发等，2005）。

式中：λ为残余强度系数；ε0为单元应力达到抗拉强度时的主拉应变；εr为与抗拉残余强度相对应的应变，εr＝ηε0；η为与抗拉残余强度相对应的应变系数，对于混凝土取值范围一般为1＜η≤5；极限拉应变εu＝ξε0（ξ＞η），ξ为极限应变系数；εmax为单元在加载历史上拉应变的最大值。

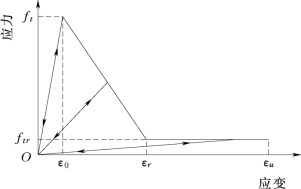
图8.2　又折线弹性损伤模型

在复杂应力状态下，拉应变由等效 拉 应 变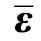代 替，即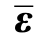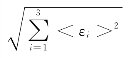＝，按照拉应力用等效拉应力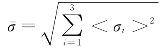，判断是否达到极限抗拉强度，其中，εi和σi分别为主应变和主应力。