如何把一个散点集合剖分成不均匀的三角形网格,这就是散点集的三角剖分问题,散点集的三角剖分,对数值分析以及图形学来说,都是极为重要的一项预处理技术。
假设V是二维实数域上的有限点集,边e是由点集中V的点作为端点构成的封闭线段,E为e的集合。那么该点集V的一个三角剖分T=(V,E)是一个平面图G,该平面图满足条件:
(1)除了端点,平面图中的边不包含点集中的任何点。
(2)没有相交边。
(3)平面图中所有的面都是三角形面,且所有三角形面的合集是散点集V的凸包。
在实际中运用最多的三角剖分是Delaunay三角剖分,它是一种特殊的三角剖分。
假设e为E中的一条边(两个端点为a,b),e若满足下列条件,则称为Delaunay边:存在一个圆经过a,b两点,圆内(注意是圆内,圆上最多允许三点共圆)不含点集V中任何其他的点,这一特性又称空圆特性。
如果点集V的一个三角剖分T只包含Delaunay边,那么该三角剖分称为Delaunay三角剖分。要满足Delaunay三角剖分的定义,必须符合两个重要的准则:
(1)外接圆准则(空圆特性)。Delaunay三角形网是唯一的(任意四点不能共圆),在Delaunay三角形网中任一三角形的外接圆范围内不会有其他点存在。
(2)局部优化准则(最大化最小角特性)。在散点集可能形成的三角剖分中,Delaunay三角剖分所形成的三角形的最小角最大。从这个意义上讲,Delaunay三角网是“最接近于规则化的三角网”。具体地说,就是两个相邻的三角形构成的凸四边形的对角线,在相互交换后,六个内角的最小角不再增大。
Delaunay三角剖分有以下特点:
(1)最接近。以最近临的三点形成三角形,且各线段(三角形的边)皆不相交。
(2)唯一性。不论从区域何处开始构建,最终都将得到一致的结果。(https://www.xing528.com)
(3)最优性。任意两个相邻三角形形成的凸四边形的对角线互换,两个三角形六个内角中最小的角度不会变大。
(4)最规则。如果将三角网中的每个三角形的最小角进行升序排列,则Delaunay三角网的排列得到的数值最大。
(5)区域性。新增、删除、移动某一个顶点时只会影响临近的三角形。
(6)具有凸多边形的外壳。三角形网最外层的边界形成一个凸多边形的外壳。
Delaunay剖分是一种三角形剖分的标准,实现它有多种算法,基本思想是:
(1)构造一个超级三角形,包含所有散点,放入三角形链表。
(2)将点集中的散点依次插入,在三角形链表中找出其外接圆包含插入点的三角形(称为该点的影响三角形),删除影响三角形的公共边,将插入点同影响三角形的全部顶点连接起来,从而完成一个点在Delaunay三角形链表中的插入,如图7.13所示。
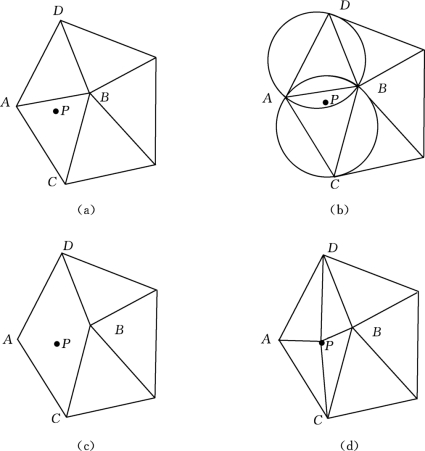
图7.13 插入新点形成新的三角形
(a)插入新点P;(b)决定如何连接P点和其他项;(c)删除AB边;(d)形成三角形
(3)根据优化准则对局部新形成的三角形进行优化。将形成的三角形放入Delaunay三角形链表。
(4)循环执行第(2)步,直到所有散点插入完毕。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




