边界拟合坐标变换理论的优化方案

通常，在利用有限差分求解偏微分方程时，需要在边界附近进行插值计算，这往往会给最终解答带来严重误差。在20世纪70年代，Thompson等（1974、1977）提出了一种基于偏微分方程法的映射方法，即边界拟合或称贴体坐标变换方法，并应用于航空航天领域，生成贴体坐标差分网格求解绕流问题。该方法通过数值求解偏微分方程而得到参数空间与物理空间之间的坐标映射关系。陈肇和等（1986、1988、1990）将边界拟合坐标方法引入计算水力学领域，用于求解WES堰上水流和土石坝渗流计算问题，马怀发（1996）在此基础上，基于该算法生成了结构性有限元网格。

边界拟合坐标变换采用Poisson方程作为物理域坐标与变换域坐标的对应关系，即

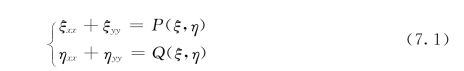
边界条件为　

式（7.1）右端的非齐次项分别为

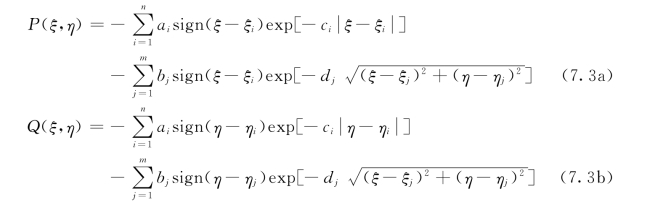
利用P（ξ，η）和Q（ξ，η）调节物理域网格位置。式中常数ai、bj是调整幅值，控制调整量的大小。ci和dj反映网格疏密变化快慢程度。式（7.3a）和式（7.3b）右端第一项分别表示ξ＝const的网格线向ξ＝ξi坐标线靠拢，η＝const的网格线向η＝ηi坐标线靠拢；第二项表示向网格点（ξj，ηj）靠拢。

通过坐标变换，将xy平面（物理平面）上的任意不规则区域D变换成ξη平面（变换平面）上的规则变换域D*，域D上的曲线边界也变换为域D*上的直线边界，如图7.1所示。在进行坐标变换时，在变换域D*上形成单位长度的正方形网格，而在物理域D上将形成贴近曲线边界的不规则四边形网格，这两种网格一一对应，均由坐标（ξ，η）的等值线构成。坐标（ξ，η）即所谓的边界拟合坐标。

(www.xing528.com)

图7.1　边界拟合坐标变换示意图

（a）物理平面；（b）变换平面

物理域D和变换域D*上各点的位置分别由其笛卡尔坐标（x，y）和边界拟合坐标（ξ，η）所确定，而求解偏微分方程（物理方程）的工作将在变换域D*上进行。在变换域D*中，式（7.1）变为

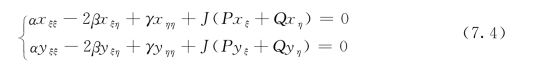
其中　

式（7.4）即为定义在变换平面上的坐标变换方程组。边界条件式（7.2）变为

在域D*的正方形网格上，用差分法计算式（7.4）、式（7.5）所得x、y值就是与正方形网格对应的物理域D中不规则四边形网格点的坐标。在域D上，边界上的网格点与边界线相吻合，在进行差分数值求解引入边界条件时无需插值，故提高了计算精度。

由于边界拟合坐标变换生成了结构性差分网格，通过适当的编码变换就可以生成有限元网格单元编码和结点编码（马怀发，1996），即利用边界拟合坐标变换自动生成有限元网格和编码，而在物理域上用有限元法解物理方程。