随机凸多面体骨料模型探究

6.4.3.1　点侵入凸体空间的判别准则

根据空间向量的混合积原理，可以判断一点是否在凸体空间内。向量的混合积将产生一体积标量，由此可以空间体积为标度建立一点是否侵入凸体空间的判别准则（刘光廷等，2003）。如图6.10所示凸体ABCDEF，假定P（x，y，z），A（x1，y1，z1），C（x2，y2，z2），B（x3，y3，z3），则四面体PACB的体积为

点P在外部与三角形ACB面围成的四面体体积为正值，若P在凸体内部则与三角形ACB面围成的四面体体积为负值，显然P在凸体的边界上时该四面体体积为零。即定义点P是否在凸体内部的判别准则为

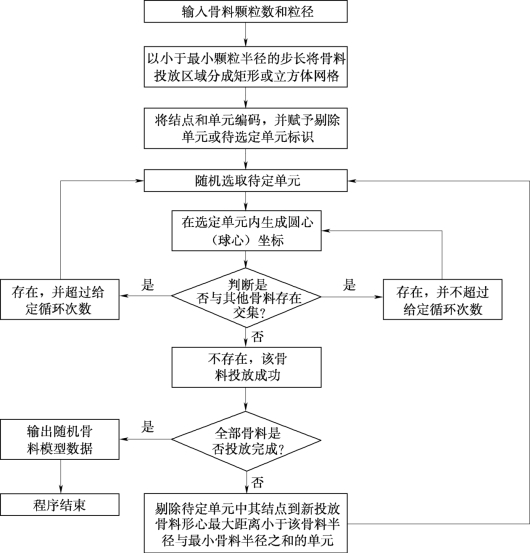
图6.9　球骨料投放程序框图

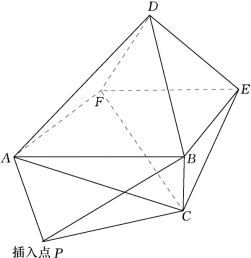
图6.10　点与空间凸体的关系

式中：Ω为凸体围成的空间区域；ΓΩ为凸体的边界面；VP为点P与面单元围成的四面体体积，凸体三角形面单元顶点由外部向内部看为逆时针排序。

6.4.3.2　三维空间两个三角形的相交检测

在空间凸多面体的延伸过程中，判断两个凸多面体之间是否相交，归根结底是进行三维空间两个三角形之间的相交检测（吕秋灵，2002），在网格剖分中，判断界面单元与骨料是否相交也要用到三维空间两个三角形之间的相交检测，这是一个重要的基础算法。

如图6.11所示，△abc位于m平面内，△def位于n平面内，两个三角形的相交检测算法如下。

图6.11　三维空间两个三角形的相交检测

对于△abc，要验证△def是否与之相交，只要验证△def的三条边是否穿过△abc即可，以de边为例：

（1）先求△abc的法向矢量M。

（2）分别求出d点到a点的方向矢量da和e点到a点的方向矢量ea。

（3）分别求出方向矢量da、ea与M的点积，即DA＝da·M，EA＝ea·M，如果DA，EA同号，说明d，e两点位于△abc平面的同侧，显然不会与△abc相交。(www.xing528.com)

（4）若DA，EA异号或有一个为零，说明de边将穿过△abc平面，此时做进一步判断，求出de边与△abc平面的交点，若交点位于△abc内（或边上），则说明△abc与△def相交。若DA，EA同时为零，即意味着de边与△abc共面，按不相交处理，由△def的相邻三角形可做出进一步判断。△def只要有一条边与△abc相交，则两个三角形相交。

（5）对如图6.11所示的情况，△def的三条边都与△abc不相交，但两个三角形仍可能相交。这时需按照上述步骤，重新判断△abc的三条边是否与△def相交即可。

（6）在上述反复循环验算的过程中，只要有一个三角形的一条边与另一个三角形相交，即可跳出程序，得出两个三角形相交的结论。如果各种情况都不满足，则两个三角形不相交。

6.4.3.3　多面体随机骨料的生成

按照以上生成的球形骨料分布生成凸体骨料的算法如下：

（1）在球形骨料颗粒表面随机生成点数（大于4，并小于某个控制数N，这里取15）；首先生成位于空间不同卦限的四个点，构成四面体骨料基。

（2）加入一个新结点，允许新插入点到该骨料球心距离稍大于原球形骨料半径，若该点与已形成凸体的内部一点分属于该凸体某侧面的两侧，则该侧面为可见面，找出该点所有的可见面。

（3）将该新结点分别与这些可见面三角形各顶点连接形成新凸体侧面。

（4）调整数据结构，消除以上可见三角形侧面。

（5）返回第（2）步，直至所有结点都加入完毕。

（6）输出多面体骨料各个三角形侧面的顶点编码及坐标值。

其中，新加入点与凸体骨料基内部一点分属于三角形平面两侧的算法有两种。第一种，按点与三角形形成的四面体体积正负值判断，原理部分见式（6.18）和式（6.19）；第二种，求出两点连线与三角形平面交点，若交点位于加入点和凸体骨料基内部点中间，则说明两点分属于平面两侧；否则，则属于平面同侧。

该程序的粗框图如图6.12所示。基于图6.8（b）所示的三级配随机球骨料分布模型生成的随机凸体骨料模型如图6.13所示。

图6.12　凸多面体骨料模型生成程序框图

图6.13　三级配随机凸体骨料模型

值得注意的是，如果凸体骨料内接于原球形骨料，将球体模型变为凸多面体模型，生成的多面体骨料模型的骨料含量很难达到原球形骨料的骨料含量，除非在骨料球面上插入很多点，这样会使生成的多面体接近于原球形骨料的形状，所以在第（2）步，在满足骨料互不侵入的条件下，允许一些新插入点到该骨料球心距离稍大于原球形骨料的半径。这样就能够使新生成的多面体骨料含量达到原球形骨料的含量要求，基本上又能反映实际骨料的多面体形态。