如何生成给定分布下的随机数？

在研究混凝土骨料投放及其参数分布模型时，除常用到在区间[0，1]上服从均匀分布的随机变量外，还会用到正态分布、对数正态分布和Weibull分布。一般情况下，具有给定分布的一维随机数可利用在[0，1]上均匀分布的随机数通过某些变换产生。下面将着重介绍这些分布函数随机数的生成方法。

6.2.3.1　正态分布

正态分布函数为

这里－∞＜x＜∞，－∞＜μ＜∞，σ＞0，则x满足正态分布N（μ，σ）。

由于这种分布应用广泛，因此对这种变量的模拟人们提出了许多方法，其中坐标变换法产生随机数的速度较快、精度较高。这种方法设两个均匀分布在[0，1]区间上的随机数为un和un+1，由式（6.6）得到符合标准正态分布N（0，1）的两个相互独立的随机数yn和yn+1。

如果随机变量X是一般正态分布N（μ，σ），则由式（6.7）得到一对相互独立的随机数xn和xn+1，而且服从一般正态分布

6.2.3.2　对数正态分布

对数正态分布函数为

这里－∞＜μ＜∞，σ＞0，则ln x满足正态分布N（μ，σ）。随机变量x的均值为，方差(www.xing528.com)

对数正态分布变量随机数产生的方法是由均匀随机数变换为正态分布随机数，然后再转换为对数正态分布随机数。

设X服从对数正态分布，随机变量x的均值为μx，标准差为σx，变异系数为Vx。由于y＝lnxn为正态分布N（μ，σ），则其标准差和均值分别为

由于y为正态分布，其随机数可由式（6.6）产生。设已得到y的随机数yi，最后可得到x的随机数为

6.2.3.3　Weibull分布

Weibull分布密度函数为

式中：x代表满足该分布参数数值；m为形状函数，m＞0；α为尺度参数，α＞0。均值，方差

由Weibull分布密度函数积分得到其分布函数

设F（xi）＝ui，即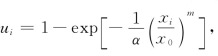ui是在（0，1）上均匀分布的随机数，可解得即有