率相关损伤模型的优化

大量的试验事实说明（王礼立等，1996），材料的流变过程总是对应或伴生着某种主导形式的材料内部缺陷或微损伤演化，直至材料破坏。在研究材料的本构关系和破坏准则时，应同时研究这类内部缺陷或微损伤的演化规律及其材料本构关系的相互影响。不同材料的试验研究一致表明，不论什么形式的材料，其内部缺陷或微损伤的演化过程都同时依赖于应变和应变率，材料的率型本构响应也常常包含了材料内部缺陷或微损伤的率型演化过程d＝d（ε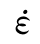，）。考虑到围压对材料损伤演化发展的限制约束作用，损伤演化方程的一般形式为d＝d（ε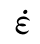，，P）（宁建国等，2006），其中P表示围压影响的参数。

朱兆祥、王礼立和唐志平（1981、1992）在研究高应变率下环氧树脂的动态力学性能时，提出了具有两个松弛时间，而材料的非线性仅与非线性弹性相关的非线性弹性本构模型，即ZWT模型，其本构关系具有以下形式

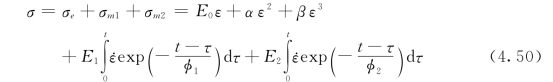
式中：E0为平衡态的弹性模量；α和β为反映材料的非线性弹性特征的材料参数，其物理模型如图4.5所示。式（4.50）中后面两个积分式分别代表具有不同松弛时间的两个Maxwell体，其中松弛时间为φ1的Maxwell体用于描述低应变率时的黏弹响应，松弛时间为φ2的Maxwell体用于描述高应变率下的黏弹响应。

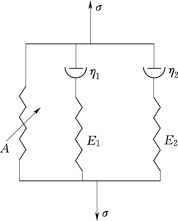
图4.5　ZWT模型

胡时胜和王道荣（2002）针对混凝土材料特性对ZWT模型进行了改进。第一，方程的第一部分σe表示与率无关的平衡态应力，由三项组成，它描述了材料的非线性的弹性。然而考虑到所讨论的混凝土材料的变形量很小，而且在准静态压缩试验中，应力应变曲线几乎是线性的，因此平衡态应力σe可考虑只取一项，即可把弹性部分看作线性的；第二，引入混凝土材料的损伤因子d。混凝土材料的动态本构关系应包含损伤因子d这个内变量，其本构方程可表示为

式中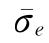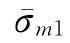：、和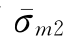分别对应σe、σm1和σm2的有效应力。

假定损伤演化函数具有经验性关系式

(www.xing528.com)

式中：Kd为损伤演化因子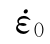；＝1/s为特征应变率；a和b为待定参数。

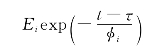是时间的递减函数，材料的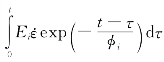反映材料响应对近期历史的敏感性比早期的敏感性强（宁建国等，2006）。

王礼立等（1996）利用热激活理论解释了混凝土材料损伤演化规律，并给出了率型损伤演化律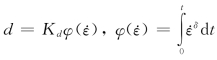：，δ为材料参数。

商霖等（2005、2006）考虑到横向约束效应即围压对材料损伤演化所起的某种限制作用，引入了如下压力相关的损伤演化因子函数

Kd（P/P0）＝a0exp（－b0P/P0）

式中：P是围压，特征围压P0＝1GPa；a0和b0为影响系数，由三轴试验或数值优化确定。

显然，在以上率相关本构模型中，假定材料具有流变松弛特性。作者认为动态加载的率效应反映在Maxwell体在短时间内无松弛响应发生，比如在高速加载过程中，可能直到加载结束，几乎无松弛变形。这种现象表现为混凝土材料在快速加载条件下较在慢速加载条件下具有较高的强度和刚度。ZWT模型中的松弛响应反映了变形相对于荷载作用的滞后效应。

马怀发等（2004）在对混凝土动态力学性能进行细观数值模拟分析时，提出了既能反映混凝土及其细观各相材料在荷载作用下的损伤演化过程，又计及应变率强化效应的损伤模型

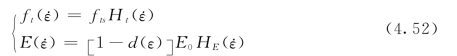
式中：E0为初始弹性模量；d（ε）为损伤变量，是拉应变的函数；fts为混凝土材料的静态抗拉强度；ft）及E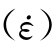）表示混凝土动抗拉强度和动弹性模量是拉（或压）应变率的函数；Ht为混凝土抗拉强度的强化系数，是在某一应变率下动态抗拉强度与静态抗拉强度的比值或称相对抗拉强度；HE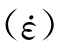为弹性模量强化系数，是在某一应变率下动态弹性模量与静态弹性模量的比值。HE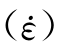和Ht强化参数反映损伤滞后效应所表现出的率强化效应。

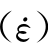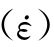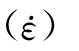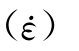式（4.52）模型的优点是，d（ε）可以采用率无关的损伤模型即静态损伤模型，而强化系数Ht）和HE）曲线，可通过第2章的简单动态加载试验的观测成果拟合得到，具有良好的试验基础。但是，HE和Ht为应变率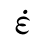的单调增函数，在动态单调加载条件下可以近似适用，但在持续时间较长的往复加载工况下的适用性还有待进一步探讨。