弹塑性损伤模型优化方案

根据热力学第二定律（即Clausius-Duhem不等式）及（弹性）应变等效假定，可得混凝土弹塑性损伤本构关系的一般形式如下

混凝土内部微裂缝引起的损伤在宏观上可定性解释为：在开始加载阶段，微裂缝处于均匀分布状态。在每一独立的微裂缝周围有一应力释放区，即损伤区，损伤区的应力为零。继续加载，应力释放区增大，独立裂缝开始连通，直到最后形成宏观裂缝，造成局部破坏。由于损伤区的应力为零，所以损伤材料的不可恢复变形完全发生在材料的无损部分（实际承担荷载部分），因此，Ju模型（1988）、Faria模型（1998、2004）和Lee-Fenves模型（1998）在有效应力空间利用塑性力学方法，即用有效应力张量代替经典塑性力学中的柯西应力张量，来考虑不可恢复变形，由于有效应力随着弹性应变的增加而单调增加，所以屈服面一直膨胀，不会出现柯西应力空间材料软化导致的屈服面收缩情况，因此只需考虑应力强化，避开了处理软化段的麻烦。但由于σ＝（1－d），所以损伤演化不仅对材料的弹性特性有影响，还会影响到塑性特性。

由于损伤变量D和塑性应变张量εp为内（状态）变量，所以上述本构关系不能完全确定材料的应力—应变关系，还需给出其中内变量的演化准则。不同的内变量演化法则将导致不同的本构模型。另外，对于损伤变量定义的合理与否也至关重要。基于4.3节应力张量及自由能势分解的基础下面简要介绍弹塑性损伤模型的框架（Faria et al.，1998、2004；吴建营，2004）。

4.4.3.1　混凝土的损伤准则

基于混凝土的损伤机制，在不考虑高静水压力导致的应变强化的前提下，混凝土材料的损伤和破坏主要源于两种不同的微观物理机制，即受拉损伤和受剪损伤。由式（4.35）和式（4.36）得到对应受拉损伤变量d+和受剪损伤变量d－的能量耗散率

混凝土的受拉损伤和受剪损伤准则可定义为如下形式

式中上标±分别对应受拉和受剪；下标n∈R+表示当前计算时刻，为当前时刻对应的损伤阈值。当损伤能释放率超过材料的初始损伤阈值r时，材料才开始产生损伤。初始损伤阈值为材料的属性，可由单轴拉、压试验确定。

如果取G±（Y±）和G±（r±）分别为Y±和r±的单调增函数，混凝土的损伤准则式（4.38a）有如下等价形式

即当损伤能释放率G±（Y±）超过材料的初始损伤阈值G±（）时材料才开始产生损伤。G±（Y±）可写成如下形式

如果不考虑混凝土受拉应力作用所发生的塑性变形，正的应力张量产生的自由能势由式（4.35）求得，则

如果考虑塑性损伤能释放率，负的应力张量产生的自由能势由式（4.36）求得

其中，（εe）、（εe）分别由式（4.33）和式（4.34）给出，而（qp）与塑性势函数的选择有关。

4.4.3.2　混凝土的损伤演化法则(www.xing528.com)

由式（4.38），可得

类似塑性理论，按正交法则有

为损伤一致参数，根据Kuhn-Tucker关系，用来定义损伤加载、卸载条件

卸载或中性变载时，g±（，）＜0，可以得到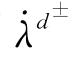＝0，d±＝0。

损伤加载时，＞0，可得，可以通过一致条件求得，即由得

将＝对时间积分，并考虑初始条件，可以得到

对上式积分，并考虑初始条件＝0，可得到损伤变量的显式形式：d±＝G±（）；

由损伤变量d±的特点，函数G±（）必须满足以下条件：，由此可假定d±的表达形式为

其中是的正值函数，反映材料的硬化、软化特性。d±可用混凝土材料的单轴受拉和单轴受压试验确定。

4.4.3.3　塑性变形

在有效应力空间考虑塑性变形，按增量理论（流动理论）描述材料在塑性状态时应力与应变速率或应变增量之间关系的理论。增量理论是在屈服面和正交流动法则基础上建立起来的，主要有四个组成部分：屈服准则、强化法则、加载—卸载准则、流动准则。在求得损伤和应变增量特别是塑性应变增量后便可求得名义应力即柯西应力。

应该注意，弹塑性损伤模型中的塑性流动需要屈服面和正交流动法则假设，对于混凝土材料这样的假设值得商榷，在混凝土材料损伤破坏过程中这样的屈服面可能并不存在。另外，在损伤演化模型中也类似地引入了损伤面和损伤面扩张的正交法则，也缺乏试验依据。