等效假定与勒梅特应变等价原理

4.3.5.1　应力等效假定

定义ε为名义应变，σ为名义应力或柯西应力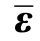，为有效应变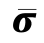，为有效应力。如图4.3所示，在实际物理空间上的名义应变ε作用在受损材料上所产生的应力与有效空间上的有效应变所产生的应力等价。

图4.3　应力等价假定示意（Simo and Ju，1987）

（a）物理空间；（b）有效（虚拟）空间

如果还是取式（4.3）中的损伤影响张量M（D），则有

如果损伤变量为标量，M（D）＝（1－d）I，有效应变＝（1－d）ε。

将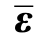＝Λ0∶σ和ε＝Λ∶σ代入式（4.20），得：Λ＝M－1（D）∶Λ0，其中，Λ和Λ0分别为有损伤和无损伤材料的柔度张量。对于一维均匀损伤，有损伤和无损伤材料弹性模量为

4.3.5.2　应变等效假定

如图4.4所示，在实际物理空间上作用在受损材料上的真实应力σ所产生的应变与有效空间上的有效应力所产生的应变等价，即勒梅特应变等价原理（Lemaitre，1971）。在有塑性应变时，勒梅特应变等价是弹性应变部分等价。

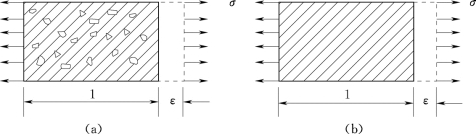
图4.4　应变等价假定示意（Simo and Ju，1987）

（a）物理空间；（b）有效（虚拟）空间

类似地，由应变等效假设，ε＝Λ0∶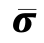＝Λ∶σ，＝M－1（D）∶σ

则有

ε＝Λ0∶M－1（D）∶σ ＝Λ∶σ

即

(www.xing528.com)

按照勒梅特应变等价原理其有效应力用无损材料中的应变ε表示，即损伤变量可表示为，其中E0为初始弹性模量，E为损伤后的弹性模量。其优点是可经过简单试验宏观可测损伤变量。

在复杂应力条件下受损材料的弹性本构方程和有效应力张量分别为

如果损伤张量D的主轴与柯西应力和有效应力的主轴重合，且主方向损伤之间不耦合，即

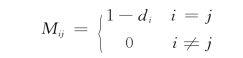
有效应力

由式（4.22）可知损伤后的刚度与初始刚度的关系为S＝M（D）∶S0，由此式（4.23）可写成

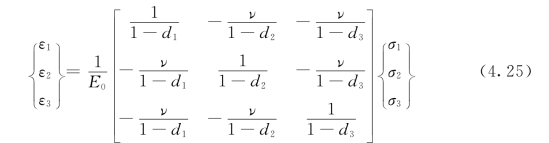
只有当d1＝d2＝d3时，损伤后的刚度张量才是对称张量。由应力等效假定得到的损伤后的刚度张量也是如此。

4.3.5.3　能量等效假定

将有效应力代替柯西应力，假定受损材料的弹性余能与相应的无损材料的弹性余能相同（Sidoroff，1981）。即

ψe（σ，D）＝ψe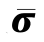（，0）

受损材料的弹性余能：

无损材料的弹性余能：

将＝M－1（D）∶σ代入式（4.27），得：，其中M－T（D）为M－1（D）的转置矩阵。损伤后的柔度张量为

损伤后的刚度张量为

显然Λ和S为对称张量。

能量等效假设可适用于各向异性材料的各向异性损伤，而应力等效假设和应变等效假设仅能应用于各向同性材料的各向同性损伤情况。另外，Soh等（2003）提出了位移等效假设，在这里不再详述。但位移等效假设克服了上述三种假设的缺点，值得参考。位移等效假设考虑了泊松效应，而应力和应变等效没有考虑。根据位移等效，在无损构形中有效应力引起的侧向变形发生在有效面积上，由于损伤构形中的名义面积大于有效面积，所以在名义面积上的平均侧向变形减小，因此，损伤构形的侧向应变小于无损构形的侧向应变，泊松比减小；而按照应变或应力等效假设两者相同，泊松比不变。位移等效在一定程度上考虑了损伤引起的能量耗散，而应力等效、应变等效、能量等效没有。