损伤滞后效应：原理及应用探究

这一节主要介绍Eibl等（1989，1999）提出的混凝土率敏感性本构关系，借此研究成果探讨动载作用下混凝土动态损伤的滞后效应机制。

Eibl等认为混凝土动态本构关系应该包括整个加载历史，惯性效应使变形及由其所产生的损伤具有延迟特性，如图3.15（a）所示，一根简支试件上作用动态荷载，当达到应变率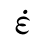＝0时的最大挠度点时，按照通常的假设，此时简支试件应该只能通过其静态强度来承载，但实际上简支试件却有更高的动态承载能力。很明显，在应变率降为0之前有更高的应变率，在更高的应变率之后一段时间才出现与之对应的最大应力。将应力和应变随时间的变化曲线放在一起比较，如图3.15（b）所示，可以更容易地看出最大应力与最大应变率在时间上并不是同时发生的。另外，当混凝土按理想的等应变率类型加载时，可以发现类似的矛盾。如图3.15（c）所示。在过渡点A时的动态强度是多大？动态强度是受左边应变率（常数），即动态强度fdyn的控制？还是受右边应变率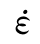（＝0），即静态强度fstat的控制？从迅速加载至A点左边到下降至A点右边的静态强度，即由动态强度到静态强度会存在一个滞后时间。

基于这些观察，Eibl等提出了一种动态损伤模型。这种动态本构关系基于图3.16所示物理模型，将试件视为由具有极限应变的弹簧耦合摩擦单元组成的并联系统。当弹簧达到极限变形后断开并激活摩擦系统和弹簧断裂端点两质点的惯性，由于惯性和摩擦作用微裂缝发展相对于静力作用时滞后，因此损伤能量将滞后释放。按照此模型，如果单元在τ时刻发生损伤，损伤增量为

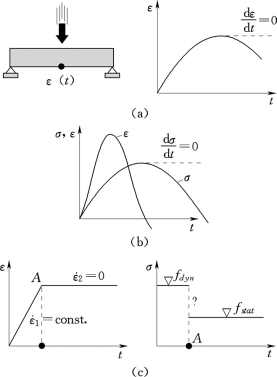
图3.15　混凝土虚拟试验分析（Eibl，1996）

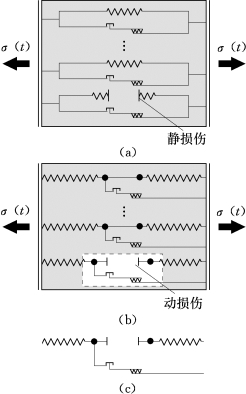
图3.16　动态损伤模型（Eibl，1996）

由于这些质点的惯性作用，使得转移的应力不会立即消失，而是过一段时间才能消失。应力减少用延迟函数g（t－τ）来表示，反映惯性作用，且函数值在0～1之间。考虑到时间的迟滞，包含动力效应的本构关系可表示为

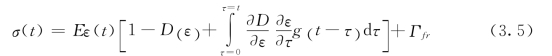
式中：为裂缝的摩擦力，损伤演化参数D（ε）和内部摩擦Dfr（ε）分别用韦伯（Weibull）分布表示为

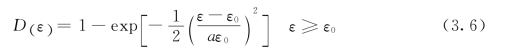
其中材料参数a决定了损伤曲线的形状，ε0是损伤演化起点的应变。破坏后的单元仍可以承受一些压力，表现为内部摩擦，随着裂缝宽度的增长逐渐消失。这种内部摩擦用另一个韦伯分布函数表示

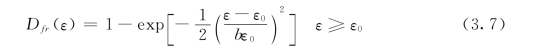
其中形状参数为b。

Eibl等（1989，1999）利用所提出的上述动力损伤模型讨论了在不同的加载历史（图3.17）工况下裂缝开展过程，用以解释惯性产生率效应的机理。

图3.17　应力—应变历史（Eibl 1996）

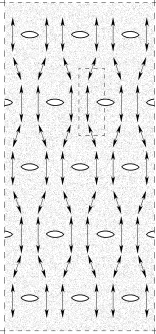
图3.18所示是在加载前具有初始微裂缝的混凝土试件的局部放大部分。试件受轴向拉力，图中箭头表示拉应力流，根据对称性从中取出矩形方框部分并进行有限元离散得到图3.19所示的计算模型。在图3.19的有限元模型中轴向分布荷载p（t）定义为外部应力，通过缝端的（A—A）横截面的应力为内部应力，取与应变率无关的静力极限抗拉强度σcr＝3.0MPa作为在微观模型裂缝增长的阈值。图3.20和图3.21给出了四种加载路径所得到的通过缝端（A—A）横截面的内部应力分布。

(www.xing528.com)

图3.18　混凝土微裂缝分布

（Eibl，1987）

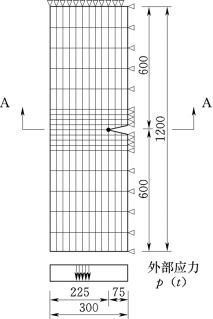
图3.19　缝端端应力分布模型（单位：mm）

（Curbach，1987）

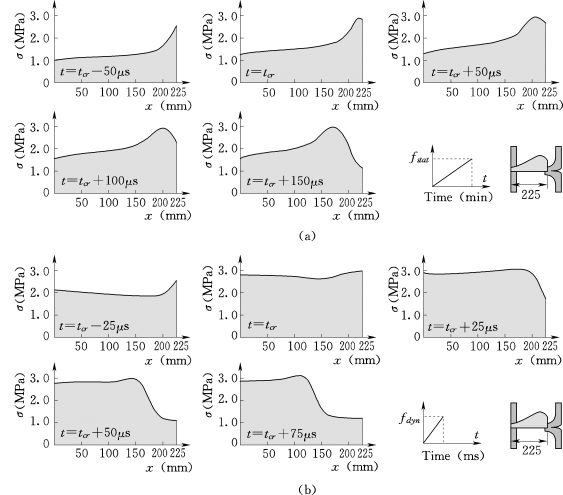
图3.20　LPⅠ和LPⅡ内部应力分布（Curbach，1987）

（a）加载路径Ⅰ（LPⅠ）；（b）加载路径Ⅱ（LPⅡ）

加载路径Ⅰ[图3.20（a）]：当t＝tcr－50μs时开始施加静载，随着荷载缓慢增加，在裂缝端部出现的应力集中如图3.20（a）所示。当t＝tcr时刻裂缝开始增长，此时预置缝顶点局部应力最大值达到极限拉强度3.0MPa，裂缝尖端开始向左边移动。最大平均应力达到2.15MPa，如图3.22（a）所示。

在加载路径Ⅱ中，快速的应力增长造成内部应力分布几乎接近均匀分布。当tcr＝0时，名义应力几乎达到了内部的最大应力3.0MPa，此时应变率为1.6/s。正如所预料的那样，由快速加载引起的应力分布要比静载下的更加均匀。

特别要注意的是LPⅢ，根据LPⅠ的结果，在t＝tcr－100μs，平均应力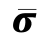为2.15MPa时，会发生静态屈服。但是，由于通过缝端的（A—A）横截面的有效应力分布大部分接近于平均应力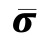，如图3.21（a）所示，因此裂缝尖端没有达到3.0MPa的应力极限。在外部应力保持为常数时，随着时间推移内部应力将重分布，即从较均匀的动态应力分布状态趋于非均匀的静态应力分布状态。从tcr－75μs到tcr－50μs，再到tcr－25μs时刻，随着时间的递增，在裂缝尖端有较高的应力峰值。图3.21（a）中用虚线表示了前一时刻的应力分布。最后，在裂缝边界上的应力超过了预定极限应力3.0MPa，裂缝开始扩展。当内部应力轮廓改变时，在不稳定的裂缝扩展引起破坏之前，平均应力仍然接近常数2.20MPa。

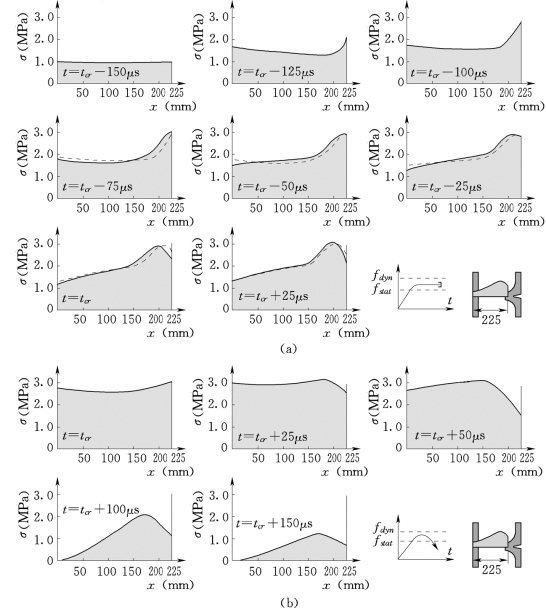
图3.21　LPⅢ和LPⅣ内部应力分析（Curbach，1987）

（a）加载路径Ⅲ（LPⅢ）；（b）加载路径Ⅳ（LPⅣ）

在LPⅣ的加载过程中，外部应力作用到时间tcr+50μs时，突然卸载之后，内部应力会重新分布，但裂缝扩展会逐渐停顿下来，直至tcr+150μs停止，最大内部应力所发生的位置在tcr+100μs后就没有变化，如图3.21（b）所示。这个现象说明，如果作用于试件或结构的荷载持续时间很短，即使这种荷载超过其静态极限强度一定范围，也不会对试件或结构造成损伤破坏。

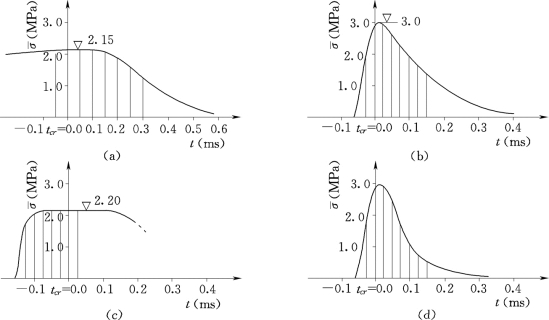
图3.22　裂缝扩展过程中外部应力的变化（Curbach，1987）

（a）加载路径Ⅰ（LPⅠ）；（b）加载路径Ⅱ（LPⅡ）；（c）加载路径Ⅲ（LPⅢ）；（d）加载路径Ⅳ（LPⅣ）

从上述研究发现，在静载作用下缝端应力集中要比动载作用下强烈。动载作用下失稳破坏时的外部应力（平均应力）高于静载作用下的外部应力，即动载强度高于静载强度。混凝土破裂过程是微观损伤连续积累的过程，微观损伤的积累导致宏观裂缝并最终导致刚度丧失。但是损伤不会在引起该损伤的荷载作用后立即产生，而是由于惯性作用暂时延迟。在高应变率下混凝土类的宏观伪均质材料特性主要是由材料微观惯性效应产生，微裂纹需要时间积累，因此，在各种应变率作用下不均匀材料的微观响应必须计及动态微观裂缝增长与时间的相关性。

尽管Eibl等的动态损伤滞后模型对混凝土的应变率强化现象作出了较为合理的解释，但是这种模型假定混凝土类材料在承受动载后的初始弹性阶段不存在应变率效应，即当应变大于极限应变后才因惯性使损伤滞后一段时间。这种因惯性所产生的损伤滞后效应通过延迟函数g（t－τ）反映出来，而延迟函数的确定带有一定的随意性，很难解释低应变率到高应变率效应过渡区的突变现象。实际上，试件在受动力作用后无论处于弹性阶段还是损伤后的非线性阶段，只要有加速度存在就会产生惯性效应。