率效应过渡区的特点与影响

混凝土应变率的宏观响应是应变率和其他各种因素共同作用的结果。从截至目前的试验成果可以发现，混凝土试件在不同的应变率范围内所表现出的动态性质不同，因此可将应变率响应区域分为静载蠕变区、低应变率不敏感响应区和高应变率敏感响应区（Rossi，1991）。

从Bischoff et al.（1991）、Malvar（1998）统计的试验结果可看出，混凝土材料无论受压还是受拉，对应变率的响应都存在以上过渡区，即在低应变率和高应变率作用下的混凝土动态性能不同，形成机理存在差异。Rossi等（1996）认为抗压强度的过渡区范围在60/s～80/s之间，而抗拉强度的过渡范围为1/s～10/s。

许多学者试图用现有的物理定律和发现来解释率效应的成因，比如3.3节～3.5节所讲述的混凝土材料对其内部含有的水和水汽的动态响应理论。在恒定静力作用下，水的存在使得湿混凝土中的凝胶体粒子分离，降低了范德华力（Wittmann，1972），在宏观上表现为湿试件的静态强度低于干试件的静态强度。在低应变率下湿混凝土的初始断裂韧度KIC下降是由于其微孔洞中水汽弥散而使固体骨架产生预应力所致。毛细水的Stefan效应提高了混凝土的动态强度已成为大多数研究者的共识。比较流行的观点是在低应变率下的动态响应主要由混凝土中毛细水起控制作用，高应变率下的动态响应主要是由于惯性力的作用。

Weerheijm（1992）把高应变率下混凝土抗拉强度的增强归于惯性效应，并认为混凝土存在最大临界开裂速率ucl，即，由纵波波速确定。

对于脆性断裂破坏，Rossi等（1995）基于试验数据，给出了开裂速度uc与应变率之间的关系式uc＝k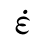m，k为常数。Anderson（1991）认为动断裂韧度与开裂速度uc有关，并定义为

断裂强度　(www.xing528.com)

B＝E/3（1－2ν）

式中：B为体积模量；E为杨氏模量；ν为泊松比；KIA为裂缝休止韧度（Arrest toughness），约为（25%～50%）KIC，当uc＝0时，KIA＝KID。

由式（3.3）可看出，当应变率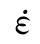接近（ucl/k）1/m时，断裂强度急剧增长。

对于湿混凝土而言，由其微空洞中的水产生的Stefan效应将在水产生空化后失效，即存在Stefan效应的休止临界应变速率。作者认为这可能是出现低应变率到高应变率响应突变的原因之一。

Eibl等（1999）基于混凝土率效应的相关研究成果认为，低应变率和高应变率以10－1/s为界，在小于和大于10－1/s两个范围内所产生的率效应是由两种不同的现象和机制控制的。在高应变率（大于10－1/s）时，率效应主要由惯性效应来控制，而在低应变率（小于10－1/s）时，率效应主要由骨料裂缝咬合、湿度等其他因素控制。