探析Stefan效应的特点

与上述蠕变效应的物理机制不同。Rossi（1991）通过试验观测和理论假设指出：混凝土在较高应变率下，其断裂韧度随裂缝开展速度增长而提高的现象可由Stefan效应以及材料的开裂过程相互作用来解释。如图3.14所示，两张平整有一定距离h的平行板，在它们之间存在一层薄黏膜（如水或油），薄黏膜两侧呈新月形，可粗略认为是圆弧形，半径为ρ，湿角为θ，板间的距离为h＝2ρcosθ，板间的液体体积为V，其黏性系数为η，表面能为γ。当以的速度分开两板时，将产生阻止两板分离的反力F，其计算式为

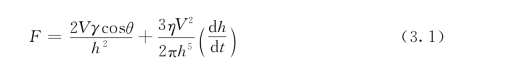
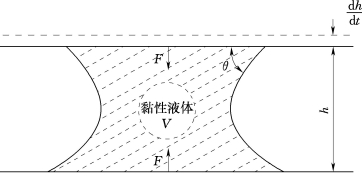
图3.14　混凝土微孔中的Stefan效应(www.xing528.com)

其中第一项为常数项，即静态毛细水吸力，在微细毛细孔径尺寸以下的孔隙中的自由水对混凝土静态强度产生主要影响，大孔隙内的自由水可以不考虑对强度的影响；第二项就是Stefan效应引起的反力，速度越大，微孔洞越细，新月形水体越大，由Stefan效应产生的反力越大。

在动力荷载下，湿混凝土中的毛细水引起的黏滞力随加载速率的增大而增加。这种黏滞力起到了阻止裂纹开裂的作用，使得混凝土的宏观等效断裂韧度和动力强度增加。而混凝土被烘干后，其中的毛细水分很少，由Stefan效应产生的影响就很小，因此干混凝土的率效应不明显。

但是用Stefan效应来解释混凝土的高应变率效应是一个大胆的假设，尚无法用理论进行验证。由于无法确定新月形水体的平均体积，Stefan效应所产生的反力很难从理论上量化。Stefan效应不会随应变率无限增长，即Stefan效应休止于微空洞中的水产生空化现象。有的学者将这个应变率阈值定为10－1/s（周继凯，2007）。