混凝土动强度试验的分析方法

混凝土材料在动载作用下所表现出的与静载作用下不同的特性，这在很大程度上取决于混凝土材料的微细观结构形态。混凝土强度是反映混凝土微细观结构特点的重要物理参数，因此，为了探寻混凝土应变率效应的内在机理，建立两者之间的定量关系，人们做了大量的试验研究工作。图2.2和图2.3所示是Bischoff（1991）等给出的不同应变率下混凝土的动态抗压强度。Bischoff指出，应变率对动态极限强度产生最重要的影响，除此以外，混凝土的品质即静载强度，对混凝土的动载强度也有重要影响。静载强度低的混凝土其动载增强因子高于静载强度高的混凝土，表现出更强的应变率敏感性，其他影响因素还有混凝土的龄期、养护条件、配合比、水灰比以及骨料类型（刚度、表面纹理、最大粒径）等。由于不同的研究者所采用的试验设备、测量方法、混凝土试件的尺寸、形状以及混凝土级配的不同，在给定应变率由不同研究者得到的混凝土动态抗压强度离散性较大，如在应变率为10/s时，在图2.2中显示出混凝土动态抗压强度增强因子（动态抗压强度与静态抗压强度之比）变化范围在1.0～2.0之间。但从总的趋势看，动态抗压强度随应变率的增加而增加，在应变率30/s左右存在一个过渡区，应变率超过这个过渡区，强度随应变率的增加而明显变大。

一般认为，动态性能中应变率效应是一个基本的材料特性。单轴动态抗拉强度有与抗压强度类似的应变率效应。Bachmann（1993）和Malvar（1998）等总结了混凝土拉伸应变率效应，如图2.4和图2.5所示。由图可看出，动态抗拉强度随应变率增加而增加，应变率效应存在某一临界值，当应变率高于这个临界值，动态抗拉强度随应变率增加而明显变大。

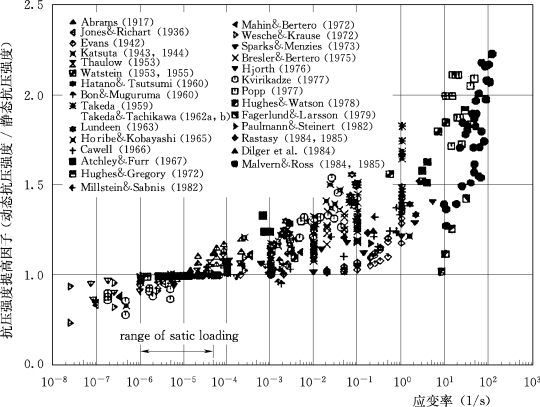
图2.2　混凝土动态抗压强度与应变率的关系（一）（Bischoff，1991）

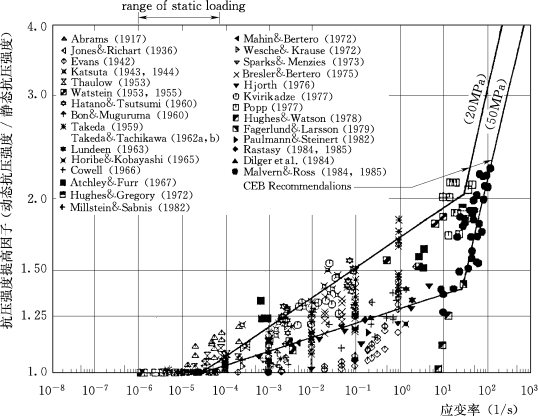
图2.3　混凝土动态抗压强度与应变率的关系（二）（Bischoff，1991）

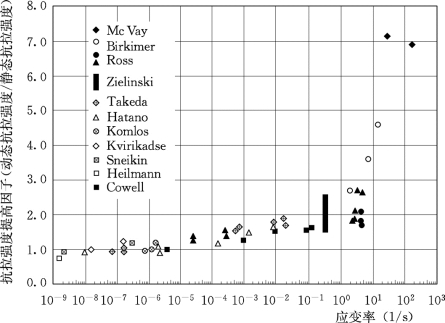
图2.4　混凝土动态抗拉强度与应变率的关系（Eibl 1999 after Bchmann，1993）

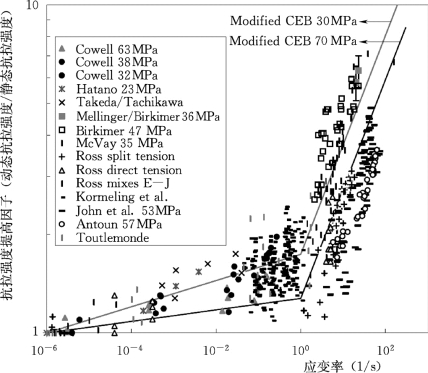
图2.5　混凝土动态抗拉强度与应变率的关系（Malvar，1998）

尽管不同试验者所得结论相差较大，但有些定性结论已基本明确：混凝土强度随应变率增加而提高，抗拉强度的率敏感性强于抗压强度，混凝土强度等级、湿度、初始静载、侧压影响其应变率敏感性。

在对这些试验研究总结的基础上，欧洲规范CEB（1993）提出了混凝土动态强度计算公式。其动态抗压强度和动态抗拉强度分别采用以下形式。

对于动态抗压强度，有

式中：fc为与响应应变率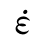相对应的动态抗压强度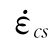；是参考压应变率，取3.0×10－5/s；lgγ＝6.156α－2；α＝（5+9fcs/fco）－1；fcs是对应应变率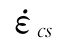的准静态抗压强度；fco＝10MPa。CEB公式斜率不连续在应变率为30/s处。CEB经验公式给出的应变率与动态抗压强度增强因子的对应关系（fcs分别为20MPa和50MPa）如图2.3所示。(www.xing528.com)

对于动态抗拉强度，有

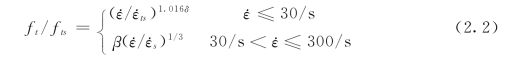
式中：ft为与响应应变率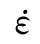相对应的动态抗拉强度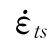；是参考拉应变率，取3.0×10－6/s；fts为与参考拉应变率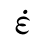ts对应的准静态抗拉强度；lgβ＝7.11δ－2.33；δ＝1/（10+6fcs/fco）；fco＝10MPa。

显然，CEB建议动态抗拉强度发生突变的应变率临界值为30/s，与动态抗压强度应变率的临界值相同。Ross（1996）的试验研究发现，混凝土动态抗压强度和动态抗拉强度都存在突变过渡区，但在受压时的临界值是受拉时的10倍。Ross假定受压时纵向裂缝是由泊松效应引起的，由此得到过渡区的临界拉应变平均值（εtc）ave与临界压应变εcc存在（εtc）ave＝0.5νεcc关系。如果泊松比ν取0.2，就有横向平均拉应变和应变率应为受压时的1/10。

因此，1998年Malvar等在总结分析了大量试验数据的基础上，提出受拉时的临界值应为1/s，并将CEB的动态抗拉强度公式修改为

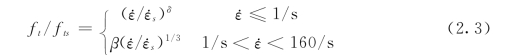
式（2.3）的适用范围为（10－6～160）/s。参考拉应变率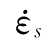取10－6/s；lgβ＝6δ－2，δ＝1/（1+8fcs/fco），fco＝10MPa。显然，式（2.3）斜率在应变率为1/s处不连续。图2.5中Malvar针对立方体抗压强度分别为30MPa和70MPa的两种混凝土给出了式（2.3）的两条曲线，在图2.5中分别标为Modified CEB 30MPa和Modified CEB 70MPa。Modified CEB 30MPa曲线在上，Modified CEB 70MPa在下方，反映出较高强度的混凝土的率敏感性低于强度较低的混凝土，这种现象在下面的章节里，作者通过数值试验可作出解释。

作者（马怀发、陈厚群等，2005）在总结有关文献和试验资料的基础上，给出以下混凝土抗拉强度与拉（或压）应变率的关系

式中：fts为混凝土材料的（准）静态抗拉强度；ftd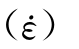表示混凝土动态抗拉强度，为拉（或压）应变率的函数；At、Bt、Ct为强度强化参数，At表示抗拉强度对应变率的敏感程度；反映抗拉强度产生率效应的最小应变率大小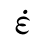，s为（准）静态抗拉（压）应变率，如果应变率小于10－6时混凝土材料的抗拉强度不产生率效应，则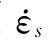取10－6，即Bt等于6；Ct反映抗拉强度对高应变率的敏感性，表现为混凝土强化曲线的曲率大小。由于不同混凝土内部结构不同，其强化系数也不同，具体问题可根据相应的混凝土材料的试验结果得到。

如果f′c＝30MPa，分别由式（2.2）即CEB公式，和Malvar对CEB的修改式（2.3），得到图2.6中对应曲线。如果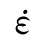s取3.0×10－6/s，①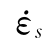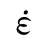＜≤30/s：At＝0.08，Ct＝1.0；②30/s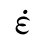＜≤300/s：At＝0.131，Ct＝6.5，由式（2.4）得到与CEB 30MPa相吻合的曲线。如果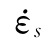取1.0×10－6/s，①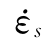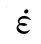＜≤1/s：At＝0.092，Ct＝1.0；②1/s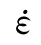＜≤160/s：At＝0.15，Ct＝4.0，由式（2.4）得到与Malvar 30MPa相吻合的曲线。这说明适当地选取参数，式（2.4）完全可以取代CEB公式和Malvar公式，即式（2.4）是CEB公式和Malvar公式的统一形式。

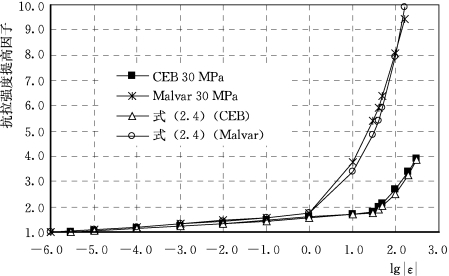
图2.6　混凝土动态抗拉强度强化曲线

另外，还有Tedesco和Ross（1998），董毓利、谢和平（1997），肖诗云、林皋（2001）等研究者提出动强度与应变率关系的对数型经验公式，其中A和B为待定常数。