动态图像边缘检测与分析技术

为了提取更好的边缘检测特征，通常需要一个深度模型，并且在分析过程中，通常会对模型进行分解，由一个模型分解为几个子模型，从而提高算法效率。例如，两个3*3可以等同于一个5*5模型。从分析和计算的角度来看，该过程是等效的，但是由于在提取过程中添加了非线性层，所以提取的图像特征更加复杂。在分析和计算的过程中，假设使用字母c表示的图像通道的数量，5×5×c=25c模型的计算量要超过2×3×3×c=18c模型的计算量。因此模型分解将有效地提高模型的计算效率。

在小样本条件下，一些更大更深的模型容易陷入过度拟合，因此在数据分析过程中应该高度重视这一现象。基于以上原因，本研究在分析模型库时，有效地结合了图像边缘库。本书的实验部分将证明，大数据量分析的优势在于，它可以最大化分层理论和最多6层的数学形态，同时提高方法的性能。在这项研究中，分形理论和数学形态学网络结构图可以参考图7.2。

图7.2　本算法的模型结构图(www.xing528.com)

在该研究中，第一层的算法由公式7.1给出。在该公式中包含的滤波器W1的数量是n1，并且模型是3*3的，可以解释为对3*3的图像块进行n1次W1分析，其分形理论和数学形态学作为该层输出的3*3个特征图的数量为n1。B1是一个n1维向量，且该层中的值是128，本算法所采用的激活模型中ReLU。

对于从第2层到第5层的模型结构，与第1层模型结构类似，如公式7.5所示：

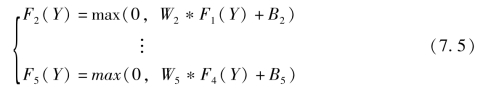
式中，W2滤波器的数量为第一层滤波器的一般，即n2=64，以此类推，第三层到第五层的滤波器数量分别为32、16和8，并且滤波器的大小为固定值，如3*3。