基于卷积神经网络的图像边缘检测方案

假设我们使用双三次插值方法对低分辨率图像进行边缘插值，产生图像边缘为Y。为了恢复边缘图像F（Y），使其无限接近原始图像X。在基于卷积神经网络的边缘检测方法中，一个分层分形理论和数学形态学模型被设计出来。从三层模型卷积神经网络与边缘检测分析过程比较中可以发现，三层模型对应三个函数，包括提取和表示函数，非线性映射函数和图像边缘分析函数。其结构如图7.1所示。

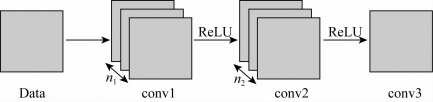
图7.1　基于卷积神经网络的三层模型

对于第一层模型，其图像块提取和表征可以通过以下公式表示：

式中，W1表示滤波器；B1表示绝对偏差；*为分析操作。并且W1包含n1 c×f1×f1个滤波器，其中c为图像中已有的通道数量，f1表示滤波器的空间域，因此W1表示对图像进行n1次分形和数学形态学分析（公式表示为c×f1×f1）。在这一层中，输出的特征数量用n1表示，在这里B1为一个向量，其维度为n1。根据该层滤波器对应元素所获取的知识，线性整流函数（Rectified Linear Unit，ReLU，激活函数）表示为max（0，x）。

在该模型的第一层中，提取图像的n1维特征向量。第二层模型从该特征向量进行映射，并从n1维映射到n2维。第二层模型可以表示为：

式中，W2包含n2个n1×f2×f2滤波器；B2是一个n2维特征向量。(www.xing528.com)

在传统算法中，预定义模式通常用于融合方法中。例如计算重叠部分的平均值。但是基于卷积神经网络的方法完全不同，它以分形理论和数学形态学生成图像块，然后对图像块进行高分辨率转换，因此为了在第三层模型中进行应用，第一个模型可表示为：

式中，W3包含c个n2×f3×f3滤波器。

基于公式7.1～公式7.3，为了获取边缘图像F（Y），分形理论和数学形态学被用来获得其模型参数Θ=｛W1，W2，W3，B1，B2，B3｝。

在基于卷积神经网络的图像边缘检测算法中，均方误差（MSE，Mean Square Error）被用作损失模型，可以使用以下表达式：

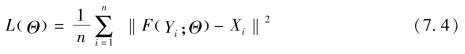
式中，n指的是要分析的样本数。

需要特别说明的是，在改模型中并没有设置池化层。该模型以上一层分析结果为研究对象，相关参数通过采样获得，同时通过采样获得平移，缩放，旋转等相关特征。在图像边缘检测方法中，其最终目标是获取更好的边缘，但是池化层将大大降低边缘检测效果，因此在本书中将不使用池化层。