模糊熵、标准差和平均目标函数的比较分析

本书第4章已经比较了非模糊方法的STD（表4.7）和MEAN（表4.8）数据，从比较结果来分析，基于GWO的相关方法在稳定性方面优于基于ABC的方法，因此本节重点分析和比较GWO及其改进方法的STD和MEAN值。

表6.7中列出了FGWOA和FMDGWOA两种方法在不同测试图像下的模糊熵、STD和MEAN值。从模糊熵的比较来看，FMDGWOA方法均优于FGWOA方法。在MEAN值的比较中，绝大多数情况下，FMDGWOA方法也高于FGWOA，但是如第4章分析的那样，MEAN只能在一定程度上反映目标函数值的优劣，在MT分割中，具有关键作用的还是最优（最大）目标函数值。因此表中列出的模糊熵的MEAN值仅作为参考。本章重点比较的是模糊熵的STD值，它反映了智能优化算法在迭代过程中的稳定性。

与FGWOA方法相比，除了阈值数量为4的Moutain图像以外，FMDGWOA方法的STD值均较小（STD越小，算法的稳定性越强）。它平均提升了18.86%，且当阈值数量为2时，Ladyhand图像获得了最大稳定性提升，提高了74.58%。因此，总体上来说，FMDGWOA方法的稳定性更好。

表6.7　FGWO和FMDGWO方法的模糊熵、STD及MEAN值比较

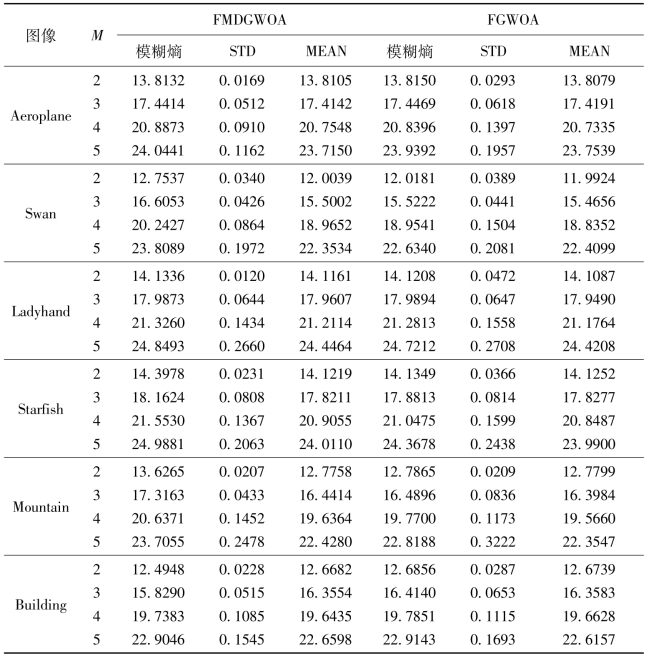
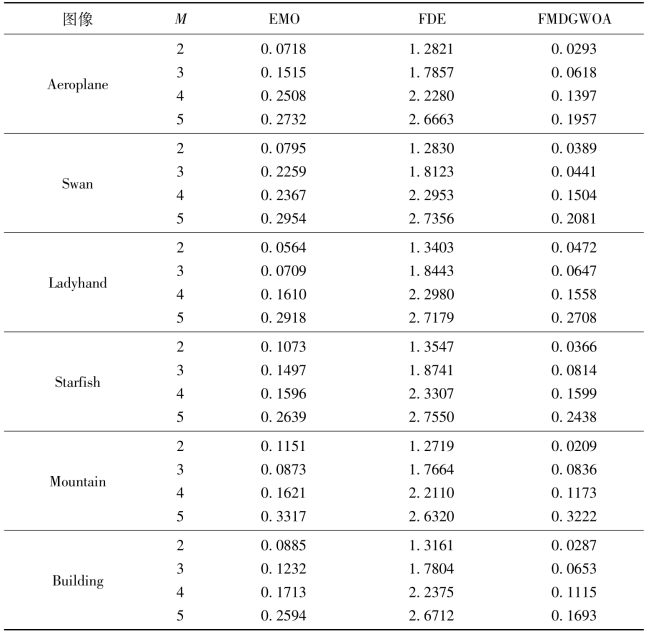
表6.8列出了前文中比较文献（EMO、FDE）和FMDGWOA方法的STD值。从表中可以看出，FMDGWOA方法的STD值均较低（STD越低，算法的迭代稳定性越好），结合表6.4和表6.5，在PSNR和运行时间方面，FMDGWOA方法明显优于EMO。而FDE的STD值明显较高，其目标函数值的迭代稳定性较差。(www.xing528.com)

与EMO方法相比，FMDGWOA的STD值平均降低了47.71%。其中，阈值数量为2的Moutain图像获得了最高的稳定性提升，提高了82.02%；阈值数量为5的Ladyhand图像提升幅度最小，提高了8.84%。

与FDE方法相比，FMDGWOA的STD值平均降低了95.68%。其中，阈值数量为2的Ladyhand图像获得了最高的稳定性提升，提高了99.10%；阈值数量为2的Ladyhand图像提升幅度最小，提高了90.21%。

综合表6.7、表6.8以及第4章表4.7的相关STD值比较，FMDGWOA和FGWOA方法在稳定性方面性能良好，均优于其他模糊和非模糊多阈值图像分割方法。尤其是FMDGWOA在稳定性方面表现更为突出。

表6.8　DE、EMO、DE和FMDGWOA方法的STD评价

结合第2章到第5章的相关方法分析，本书所采用的MQABC和MDGWO方法在模糊和非模糊多阈值图像分割方面均获得了较好的性能评价。两者比较来看，MQABC方法在运行时间方面更为突出，而MDGWO在稳定性方面效果更好。因此，MQABC和MDGWO是两种行之有效的多阈值图像分割工具。它们不仅能够保持良好的图像分割效果，而且在性能评价方面优于其他常用多阈值图像分割方法。尤其是当引入模糊理论和像素邻域信息聚合以后，FMQABCA和FMDGWOA方法在原有方法基础上获得了更高的多阈值图像分割性能。