文献[101]将图像模糊集初始化方法总结为基于直方图方法和基于质心(Centroids)方法。基于直方图的方法是一种常用的阈值化图像分割方法,但是这类方法需要预测直方图的概率分布(如高斯分布)。不幸的是,不同类型的图像其直方图的概率分布遵循不同的概率模型,如磁共振(MR)图像的直方图符合莱斯分布(RD)[191]、超声波(UD)图像的直方图符合混合高斯分布(MGD)[101],因而基于直方图方法通用性性较差。与之相对应的是,基于质心的方法可以不用考虑图像直方图的形状和概率分布,只需选择合适的质心即可。前文中所述由第5章公式5.8所获得的阈值被设置为本书的质心,以此质心为基础,通过适当模糊隶属度函数即可分配每个像素的模糊度。图5.1中给出了模糊熵所采用的梯形隶属度函数,图6.5中给出了伪梯形隶属度函数,从两个图的比较来看,梯形隶属度函数具有较多的数值为1的模糊概率,这个特点有利于在模糊优化过程中提高质心选择的精度,但是在模糊初始化过程中,较多的模糊概率1不利于模糊聚合。模糊聚合只能对非确定性模糊值进行聚合,而模糊概率为1的模糊度是一个确定性问题,原则上不需要聚合,因此为了提高模糊聚合方法的使用频率,进而提高模糊聚合效果,在模糊隶属度初始化过程中将采用图6.5所示的伪梯形隶属度函数。
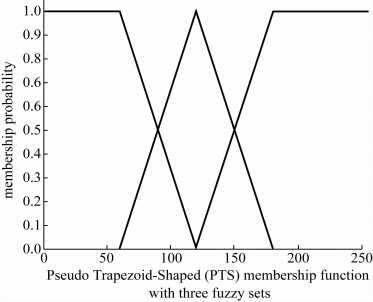
图6.5 伪梯形隶属度函数(质心分别为60、120、180)
图6.5所表示的模糊隶属度函数可公式化表示为:
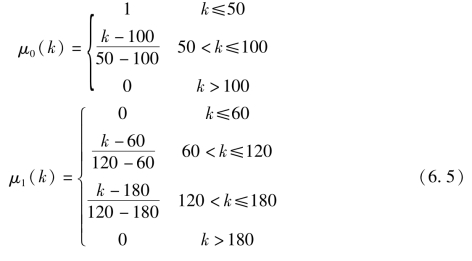
 (https://www.xing528.com)
(https://www.xing528.com)
与梯形隶属度函数(公式5.5)公式化表示类似,n质心情况下伪梯形隶属度函数的公式化表示为如公式6.6所示。

式中,μ′0(k),μ′1(k),…,μ′m(k)为像素模糊隶属度初始化函数;a1,a2,…,an为伪梯形隶属度函数的模糊参数(由公式5.8计算),即质心;k为图像中某个像素点的灰度值。
图6.5中给出了三质心情况下,像素的模糊度分配方法。假设图像I中的任意一个像素i在第r类(区域)的隶属度用μr(I(i))表示,由伪梯形隶属度函数初始化整个图像的模糊隶属度以后,每个像素对应的隶属度向量为μ(I(i)),其计算方法如公式6.7所示。
![]()
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




