基于参数的图像分割质量评价方法

本章采用PSNR来评价图像分割的质量，表4.6展示了MDGWO、GWO、EMO、DE和MQABC几种方法的PSNR值对比，表4.7所示为这些方法的STD对比，表4.8所示为这些方法的MEAN值比较。在图像分割质量方面，从表4.6可以看出，在绝大多数情况下MDGWO和MQABC方法获得了更高的PSNR值。因此，MDGWO和MQABC方法能够更好地实现图像分割，特别是当阈值数量增加时，MDGWO和MQABC方法展示了更高的PSNR值。从数据对比来看，除了使用DE算法且阈值数量为5的Lady图像，阈值数量为4的Surfing图像及阈值数量为4和5的Cameraman图像以外，MDGWO和MQABC方法均获得了最高的PSNR值。

与原始GWO方法相比，MDGWO方法的PSNR值平均提高了5.97%。其中，当阈值数量为5时，Butterfly图像获得了最大幅度的提升，提高了21.25%。MQABC方法的PSNR值平均提高了2.56%。其中，当阈值数量为2时，Butterfly图像获得了最大幅度的提升，提高了15.2%。

表4.6　不同方法的图像分割质量评价

与EMO方法相比，MDGWO方法的PSNR值平均提高了5.7%。其中，当阈值数量为2时，Surfing图像获得了最大幅度的提升，提高了39.94%。MQABC方法的PSNR值平均提高了1.75%。其中，当阈值数量为2时，Butterfly图像获得了最大幅度的提升，提高了30.16%。

与DE方法相比，MDGWO方法的PSNR值平均提高了31.14%。其中，当阈值数量为2时，Baboon图像获得了最大幅度的提升，提高了97.54%。MQABC方法的PSNR值平均提高了26.52%。其中，当阈值数量为2时，Starfish图像获得了最大幅度的提升，提高了67.19%。

与MQABC方法相比，MDGWO方法的PSNR值平均提高了3.86%。其中，当阈值数量为2时，Surfing图像获得了最大幅度的提升，提高了38.36%。

综合上述比较分析，在分割质量方面，MDGWO明显优于DE方法。与EMO、GWO和MQABC方法相比，尽管不是特别明显，但是也有不同程度的提高，因此在一定程度上反映了MDGWO方法是一种高效的MT分割方法。

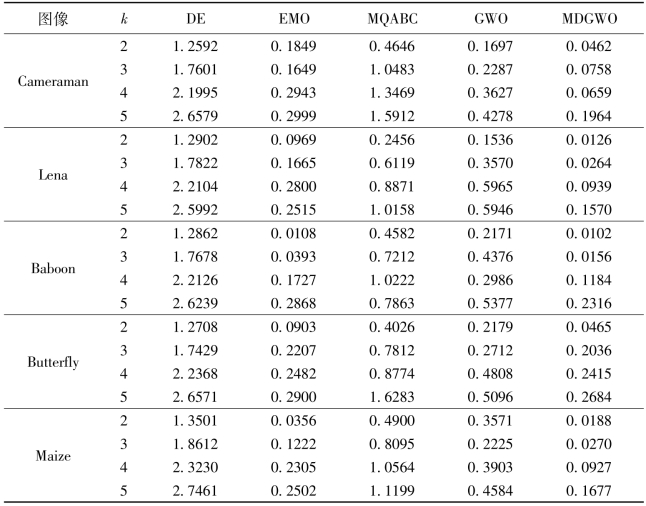
表4.7显示了不同方法的STD比较结果，标准差（STD）越小表示优化算法在迭代过程中的目标函数变化越小，即算法更稳定。从表4.7中可以看出，相较于EMO、DE、MQABC和GWO方法，MDGWO方法的STD更小，因此在算法的稳定性方面，MDGWO方法更好。

表4.7　不同方法的标准差评价

(www.xing528.com)

续表

详细的，与GWO方法相比，MDGWO方法的STD值平均提高了73.52%。其中，当阈值数量为3时，Baboon图像获得了最大幅度的提升，提高了96.44%。当阈值数量为3时，Butterfly图像的提升幅度最小，提升了24.92%。

与EMO方法相比，MDGWO方法的STD值平均提高了47.88%。其中，当阈值数量为2时，Lena图像获得了最大幅度的提升，提高了87%。当阈值数量为3时，Surfing图像的提升幅度最小，提升了0.6%。

与DE方法相比，MDGWO方法的STD值平均提高了95.60%。其中，当阈值数量为2时，Baboon图像获得了最大幅度的提升，提高了99.21%。当阈值数量为3时，Butterfly图像的提升幅度最小，提升了88.32%。

与MQABC方法相比，MDGWO方法的STD值平均提高了89.01%。其中，当阈值数量为3时，Baboon图像获得了最大幅度的提升，提高了97.84%。当阈值数量为5时，Baboon图像的提升幅度最小，提升了70.55%。

通过与DE、EMO、MQABC和GWO方法的STD比较可以看出，MDGWO方法在迭代稳定性方面明显优于其他方法。这主要归功于权重化寻优策略的改进，通过提高最优解在种群更新过程中的影响权重，极大地提升了MDGWO方法的迭代稳定性。

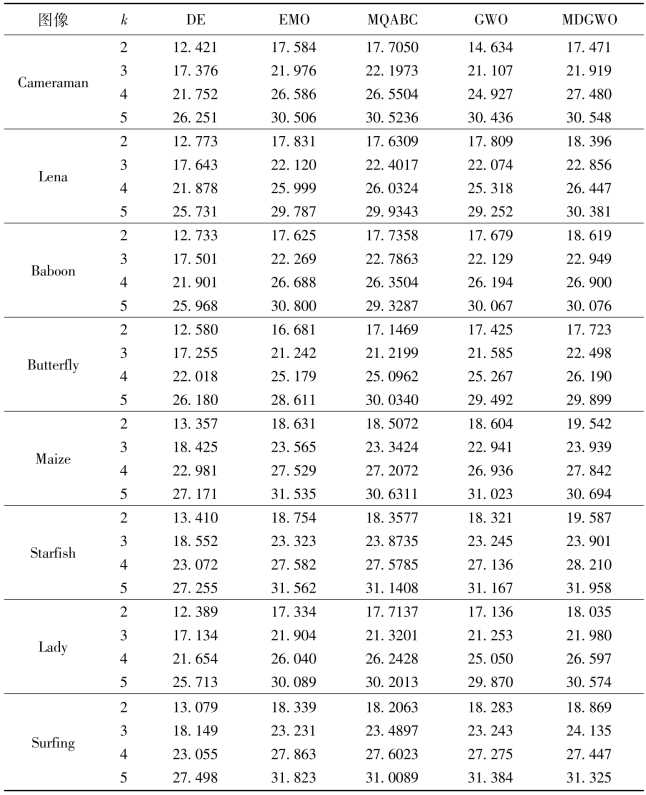
表4.8展示了不同方法的平均目标函数值，目标函数越大优化算法的优化结果越好。它也能够在一定程度上反映算法的稳定程度。但是在算法优化过程中，目标函数的极值才能准确地反映优化算法的优化程度，因此目标函数的平均值只能在一定程度上反映优化算法的优劣，却不能绝对地证明优化算法的优化程度。但是基于比较文献的数据，本书也列出了目标函数的平均值，作为辅助参数来说明MDGWO方法的模糊稳定性。从表4.8可以看出，在绝大多数情况下，相较于GWO、EMO、DE和MQABC方法，MDGWO方法获得了更高的MEAN值，即使当MDGWO方法的MEAN值相对较小时，其差别也很小，因此这也在一定程度上反映了该算法的稳定性。

表4.8　不同方法的目标函数平均值评价

综合表4.5、表4.6、表4.7、表4.8以及图4.3和图4.4的定量及视觉效果分析，MDGWO方法在MT分割中获得了更好的分割效果，并且它在优化过程、分割精度、稳定性以及鲁棒性方面具有明显的优势。因而MDGWO方法是一种高精度、高质量的多阈值图像分割方法。