MDGWO算法的迭代过程优化

经过MDGWO算法的初始化，α、β、δ和ω四个等级的狼群都被分配k个阈值组成的向量。SN个种群会组成一个SN*k维的二维向量。在算法未达到最优或者在最大迭代次数Max_iteration范围内，所有的种群在每一次迭代过程中都要更新其阈值向量。其具体的更新过程和更新方法将分三步完成：包围、追逐和攻击。

1）狼群包围行为

在自然环境中，狼群在捕食之前，首先根据猎物的位置调整各自的攻击位置，并完成对猎物的包围。在MT分割中，狼群的包围行为被抽象为阈值的自动更新（即调整阈值向量的各个阈值的大小）。算法根据新更新的阈值向量，通过适应度值（公式4.13）计算每个种群的质量。如果当前种群的适应度值超过（根据历史经验记录的前三个最优解）的适应度值，则根据其大小更新对应的前三个最优解中的某一个。包围过程的灰狼位置更新方式如公式4.15所示。

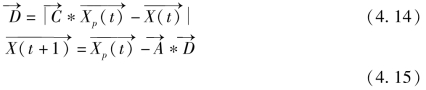
式中，t为当前迭代的序号；是由公式4.16和4.17获得的系数向量；为第t次迭代时的第p个阈值向量，p的取值范围为［1，SN］；和分别为当前迭代的阈值向量和为下一次迭代准备的阈值向量。

式中，是一个线性递减函数，它在迭代过程中逐渐从2递减至0；是［0，

1］范围内的随机向量。

2）狼群追逐行为

自然状态下，在完成对猎物的包围以后，狼群会在α狼的领导下，展开对猎物的追逐。这个过程或者缩小包围圈或者消耗猎物的精力。在灰狼算法模型中，狼群会根据在追逐过程中距离猎物的远近，分别将前三个最优位置（最优解）赋值给α、β和δ所代表的阈值向量为了完成猎物的攻击行为，除了前三个最优位置分别被赋值给α、β和δ狼以外，狼群的最大团体ω狼也会根据前三个最优解更新自己的位置，即完成对猎物的追逐锁定。在GWO中，所有灰狼种群通过前三个最优解的平均值来更新自己的种群向量，然后以不断迭代的方式逐渐完成捕猎行为。为了提高最优解的搜索速度和算法的收敛效率，本章的MDGWO不再简单地通过平均值来更新阈值向量，而是通过加权方式，提高更优解在α、β和δ位置更新中的作用。新的候选种群位置更新方式如公式4.20所示，相关系数由公式4.18计算，相关系数由公式4.19求解，其中由公式4.16计算得到，为上一次迭代的最优解。

(www.xing528.com)

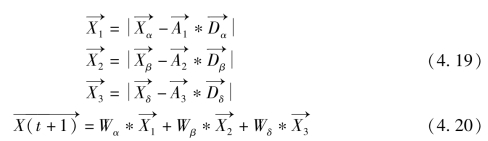
公式4.20中，Wα、Wβ和Wδ为当前迭代过程中产生的前三个最优阈值向量的权重，如公式4.21所示。

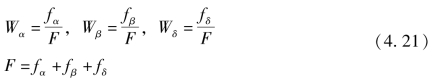
式中，fα、fβ和fδ分别为前三个最优解对应的目标函数值，由公式4.7所得。

需要重点强调的是，区别于GWO的灰狼位置更新方式，由公式4.20和4.21所示，通过加权方式进行灰狼的位置更新为本书首次采用，这也是本章MDGWO的主要贡献。

3）狼群攻击行为

当完成对猎物的追逐，且猎物停止移动时，α狼群便会发出攻击指令，包括α狼在内的狼群共同完成最后的捕猎行为。在GWO的模型中，当猎物停止移动（算法达到当前最优），α狼所表示的阈值向量即为当前最优解。在数学模型中，狼群逐渐接近猎物的过程以值的逐渐线性较小来完成。由公式4.16可以看出，当逐渐减少时，的取值也会随机变化。即在灰狼算法的迭代过程中的取值逐渐从2线性递减至0，同时也会取到［-e，e］范围内的随机值。当的值在［-1，1］范围之内时，α、β和δ狼处于当前解和最优解之间，如果的绝对值再进一步减小，灰狼算法会逐渐接近最优解，即完成捕猎，如图4.1（a）所示。

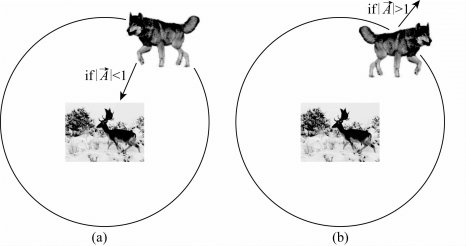
图4.1　狼群攻击行为

与之相对应的，如果猎物攻击失败或当前捕猎完成，狼群会远离当前位置，然后继续寻找其他猎物。在算法模型中，为了使反映这种情况，也为了使算法更加合理，当的绝对值大于1时，表示当前攻击完成或攻击失败。狼群会远离当前最优解，并在α狼的领导下继续搜索其他可行解，如图4.1（b）所示。