磨削温度场的有限元仿真优化

1.几何模型建立和网格划分

普通平面浅磨削时，磨削深度较小，因此在磨削温度计算与数值仿真时可认为已加工表面与未加工表面重合，热源所在表面与其运动方向平行，如图8-81所示，ϕ=0的情况。但在深磨条件下，如在大切深的缓进给磨削和超高速高效深磨中，磨削深度可达几毫米甚至几十毫米。如果将磨削接触弧简化为直线，则高效深磨时的传热情况如图8-81所示。热源所在表面与其运动方向之间有一个夹角ϕ，倾斜的平面热源一面以速度v平移，同时热源前下方的材料不断进入磨削区被去除。显然此时不能再认为已加工表面和未加工表面是同一个表面，而应根据实际情况考虑磨削深度a_p对热源运动和传热条件的影响。

根据上述分析，将高效深切磨削简化为图8-82所示，即砂轮切入区、稳定磨削区和砂轮切出区三个部分。在砂轮切入区，砂轮—工件接触弧长逐渐增大；在稳定磨削区，砂轮—工件接触弧长保持不变；在砂轮切出区，砂轮—工件接触弧长逐渐减小。各部分接触弧长计算如下

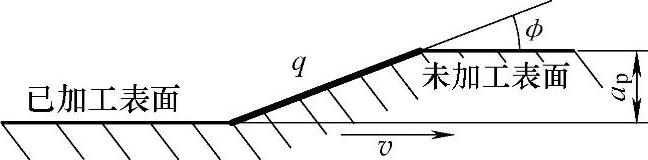
图8-81 倾斜移动热源模型

砂轮切入区

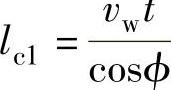
稳定磨削区

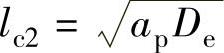
砂轮切出区

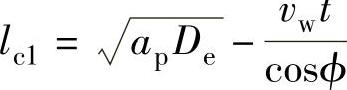
式中 D_e——砂轮当量直径；

a_p——磨削深度；

v_w——工件进给速度。

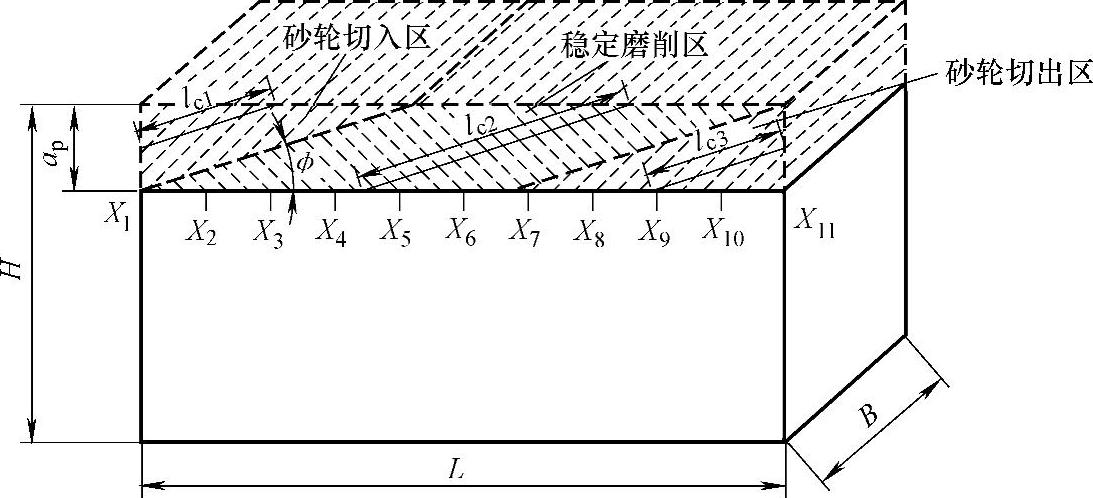
图8-82 HEDG磨削过程

在高效深磨时，由于磨削深度很大，角度ϕ非常大，磨削热源并非沿接触弧运动，而是以工件进给速度朝前方仍有材料的区域运动，同时前方被预热的材料不断被去除，即一部分从磨削区进入工件的热量在尚未向下传入非磨削区时，就被切离的材料带走。所以在建模时，可将工件划分为有限个堆叠的薄片（图8-83），运用ANSYS单元生死技术，假设薄片在每一个时间步加载后被逐步去除。为了缩短计算时间，仅取磨削工件横截面进行仿真。选择PLANE75平面热分析单元对上述几何模型进行网格划分，得到如图8-84所示有限元模型。

图8-83 HEDG几何模型

图8-84 HEDG有限元模型

2.加载求解

高效深磨的磨削深度很大，因而工件—砂轮接触弧长也很大。在接触弧上，从接触前端至末端，最大未变形切屑厚度变化非常大，因此假定传入工件的热流在磨削接触区呈三角形分布，热流最强的部分在接触区的前缘入口处，则热流分布函数如下

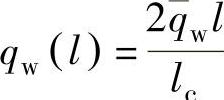
式中 q_w——平均热流密度；

l_c——接触弧长。(www.xing528.com)

利用有限元分析软件ANSYS的函数编辑器建立热流分布函数，通过DO循环实现循环加载。砂轮切入区、稳定磨削区、砂轮切出区的热流加载分别如图8-85、图8-86和图8-87所示。

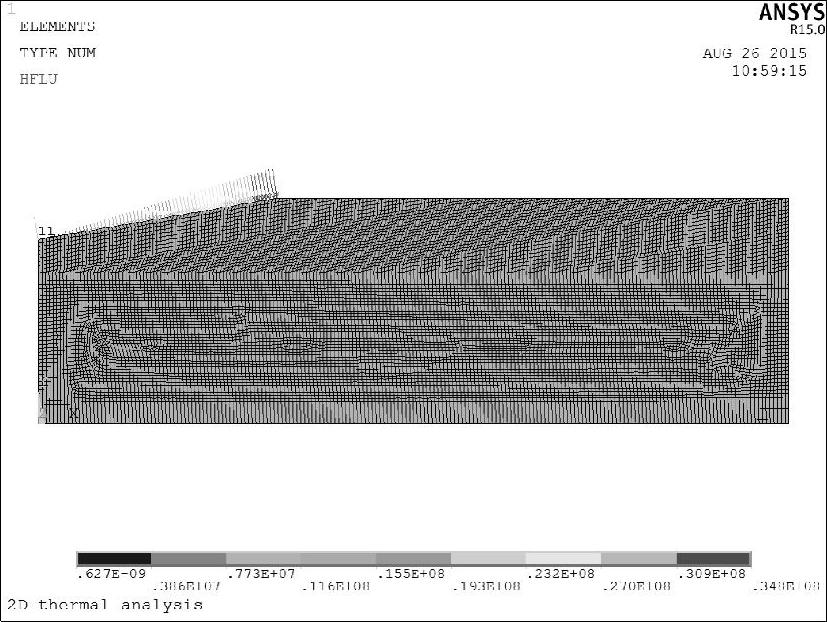
图8-85 砂轮切入区接触弧上热流分布

图8-86 稳定磨削区接触弧上热流分布

3.仿真结果

进入ANSYS软件通用后处理器，查看数值仿真结果，图8-88、图8-89和图8-90分别为三个磨削阶段工件温度分布云图，最大磨削温度出现在工件—砂轮倾斜接触面上，已加工表面的温度远低于最大磨削温度。

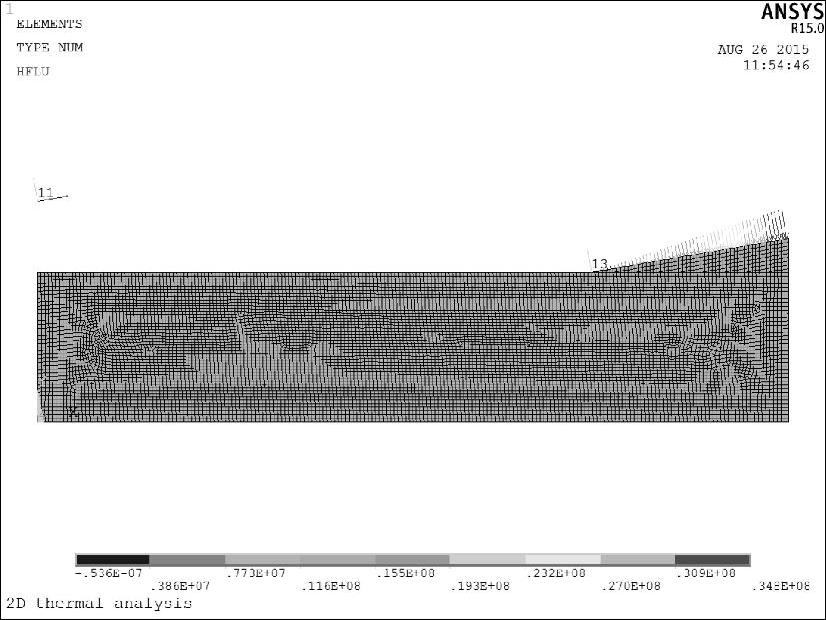
图8-87 砂轮切出区接触弧上热流分布

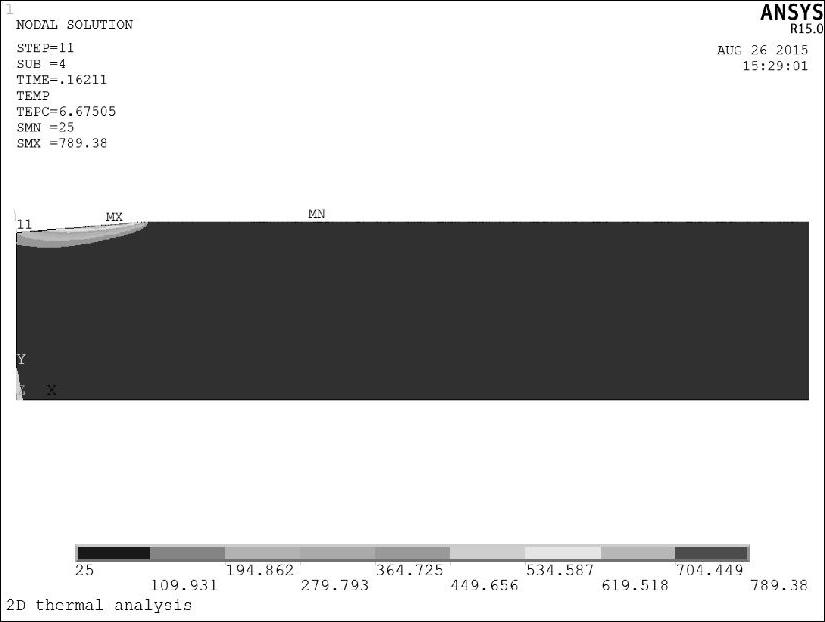
图8-88 砂轮切入阶段温度分布云图

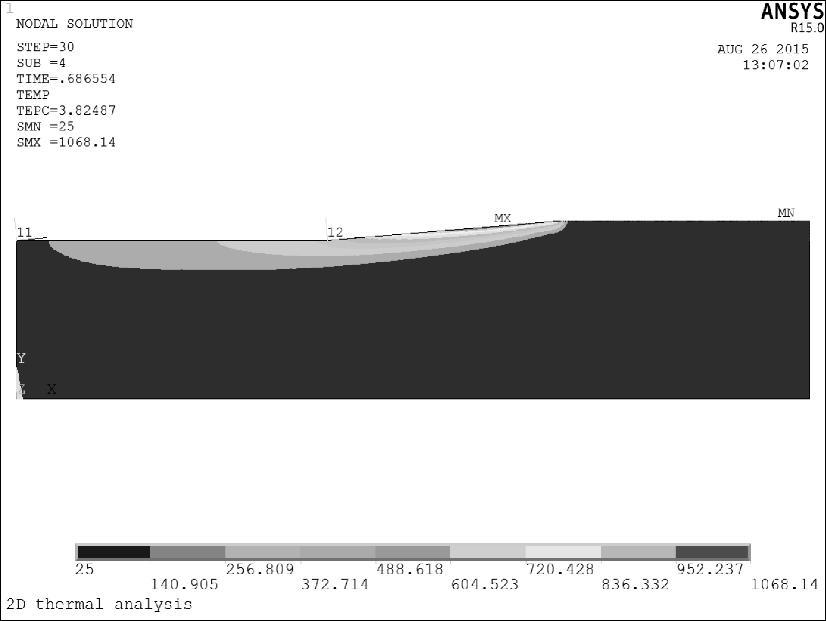
图8-89 稳定磨削阶段温度分布云图

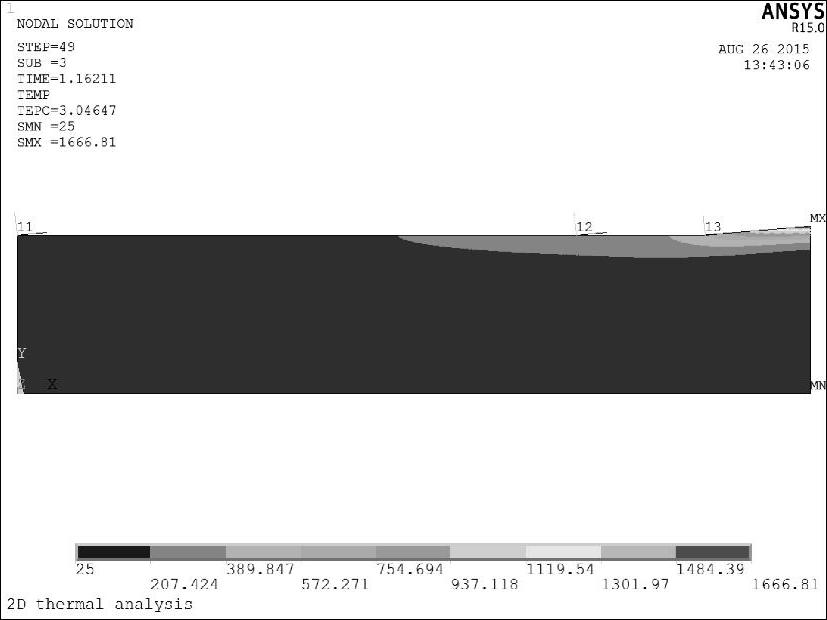
图8-90砂轮切出阶段温度分布云图

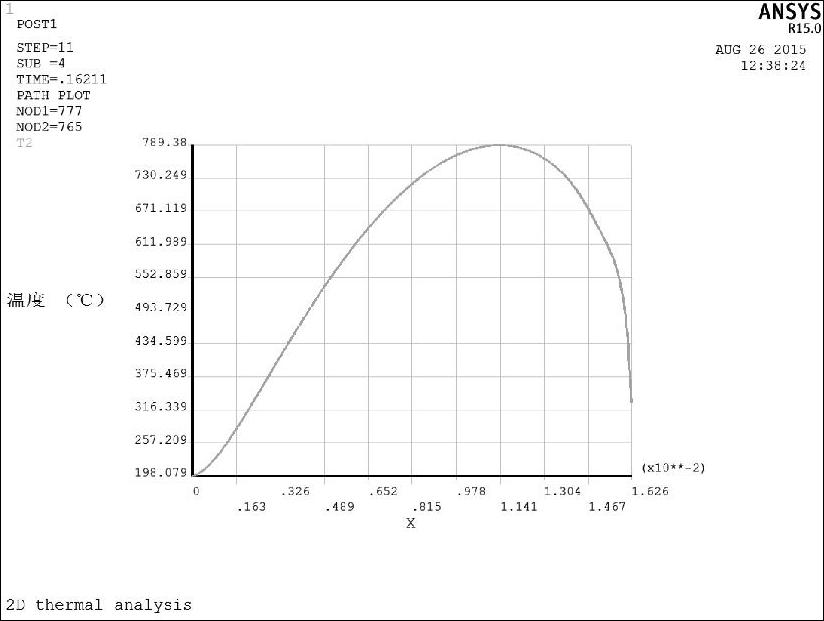
图8-91 砂轮切入阶段沿接触弧温度分布曲线

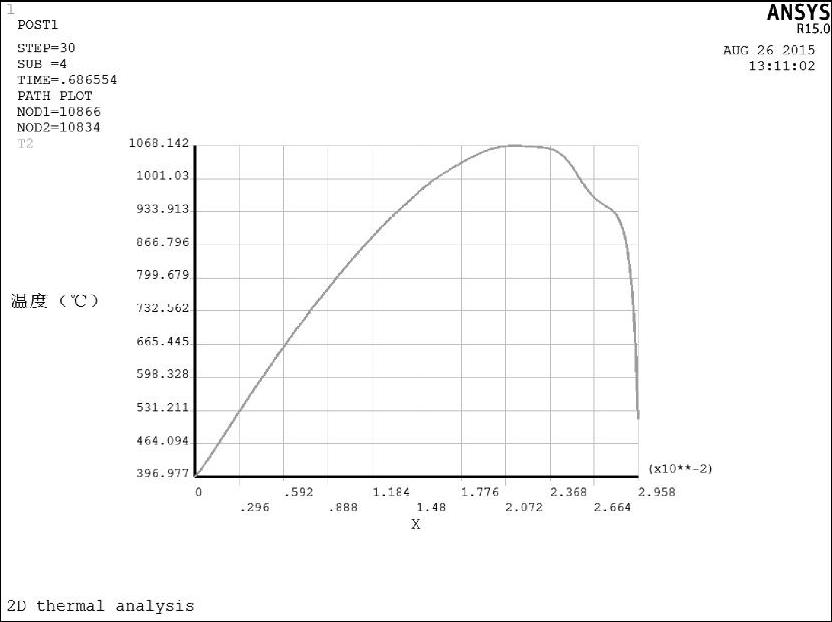
图8-92 稳定磨削阶段沿接触弧温度分布曲线

图8-91、图8-92和图8-93分别为三个磨削阶段磨削温度沿砂轮—工件接触弧的分布曲线，砂轮切入阶段和温度磨削阶段的最大磨削温度均出现在接触弧的中前部，而砂轮切出阶段的磨削温度沿砂轮—工件接触弧几乎呈线性分布，而且接触弧前端温度非常高。这是因为在砂轮切出阶段，接触弧前方已经没有材料，绝热边界的存在使得传热条件恶化，磨削热量聚集在接触弧下方很有限的材料内，使得工件温度非常高。

进入ANSYS软件时间历程后处理器，查看求解后已加工表面不同位置温度随时间的变化曲线如图8-94所示，其中X₁～X₁₁的位置如图8-82所示。

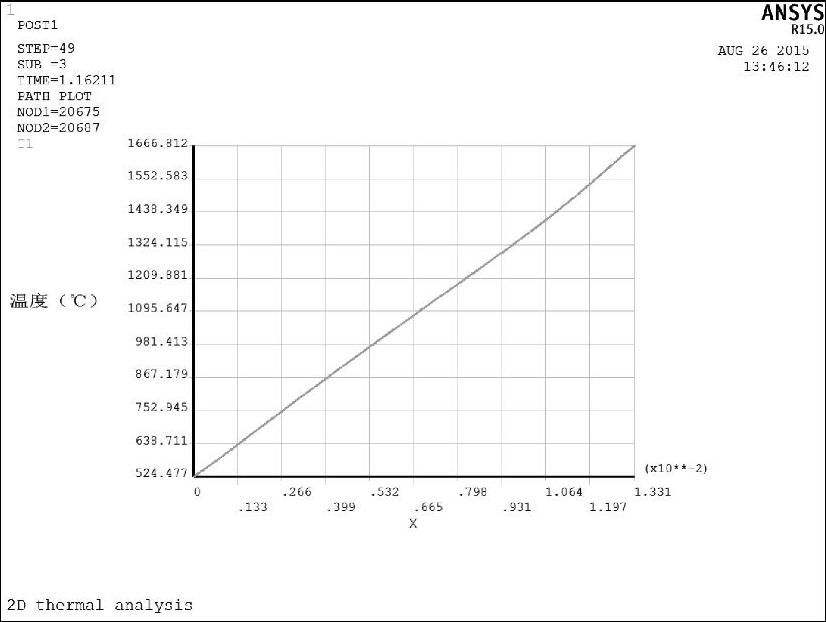
图8-93 砂轮切出阶段沿接触弧温度分布曲线

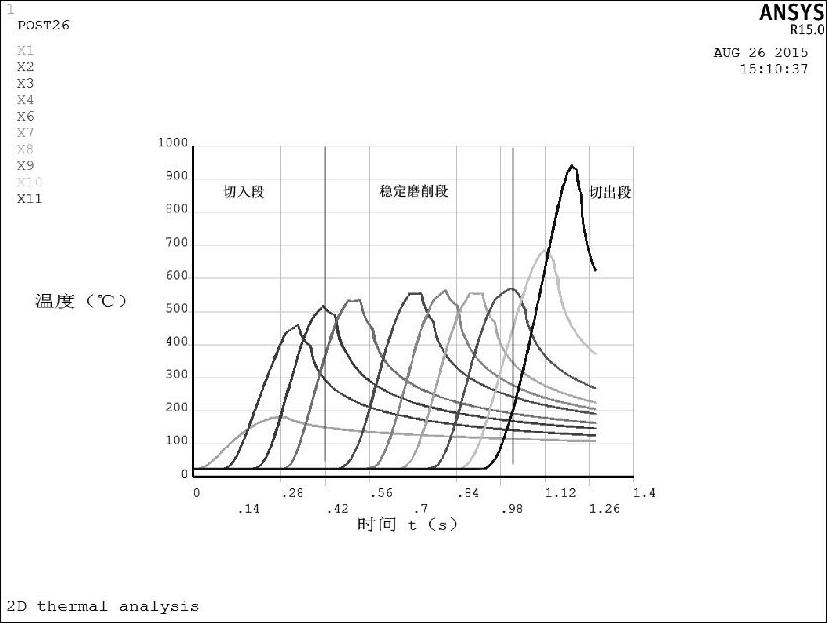
图8-94 已加工表面不同位置温度随时间的变化曲线