渐开线工件位置平均热源强度计算

根据第3章热分配子模型的分析，齿轮成形磨削过程中，齿轮轮廓渐开线上各位置的最大磨削温度可由下式计算

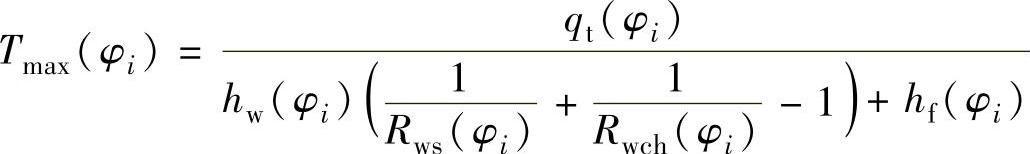
q_t（φ_i）=q_w（φ_i）+q_s（φ_i）+q_ch（φ_i）+q_f（φ_i）

q_w（φ_i）=h_w（φi）T_max（φ_i）

q_s（φ_i）=h_s（φ_i）T_max（φ_i）

q_f（φ_i）=h_f（φ_i）T_max|_Tmax≤T_b

q_ch（φ_i）=h_ch（φi）T_max（φ_i）

T_max（φ_i）和q_t（φ_i）分别是齿轮渐开线上不同滚动角位置的最大磨削温升和总的热流密度。q_w（φ_i）、q_s（φ_i）、qch（φ_i）和q_f（φ_i）分别是在齿轮渐开线上不同滚动角位置传入到工件、砂轮、磨屑和磨削液的热流密度。h_w（φ_i）为传入工件的热量传导因素

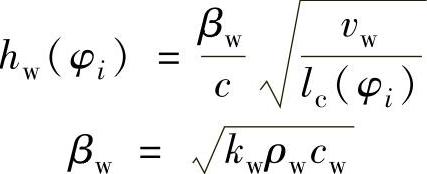
对于帕克莱数L=10的浅磨，c=1.06，对于帕克莱数L=0.1，c=0.74，在本节取c=1。

h_f（φ_i）是对流热传导因子，在干磨时认为h_f（φ_i）=0，采用油基磨削液时取h_f（φ_i）=23000。

R_ws（φ_i）——工件—砂轮子系统中传入工件的热比率，根据Hahn的模型，工件—砂轮

磨粒之间的热分配比率R_ws（φ_i）定义为

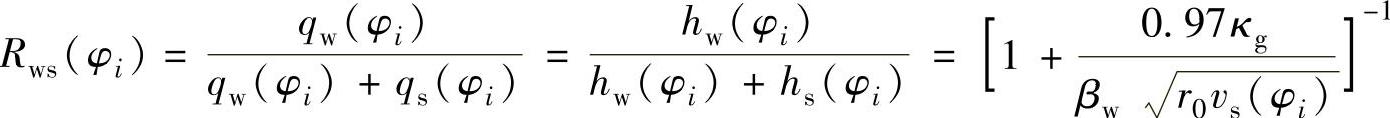
R_wch（φ_i）——工件—磨屑子系统中传入工件的热比率，R_wch（φ_i）可通过下式导出

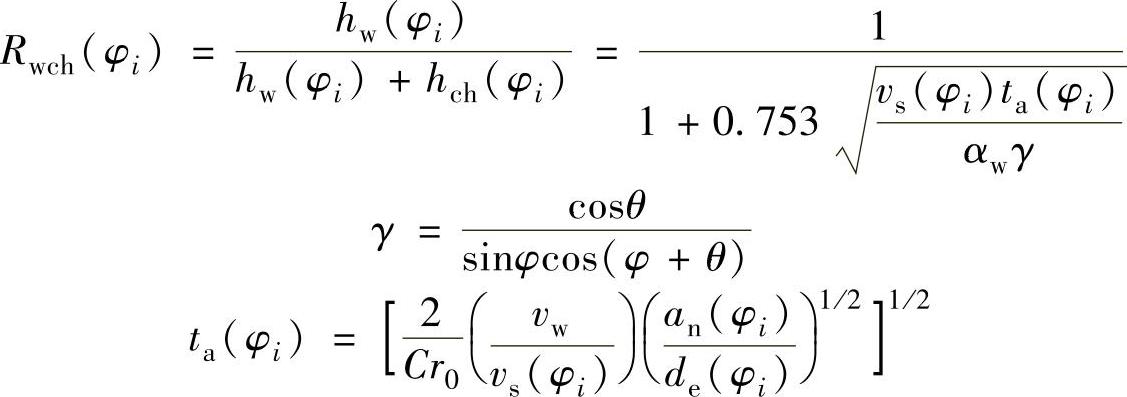
根据以上分析，齿轮渐开线上不同滚动角位置传入工件的热比率为(www.xing528.com)

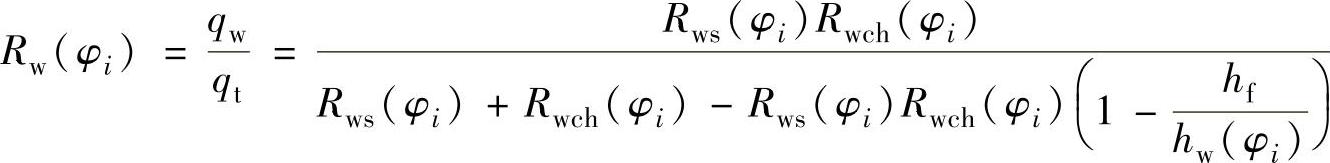
表7-9 砂轮—工件几何接触时参数与滚动角ψ_i的关系

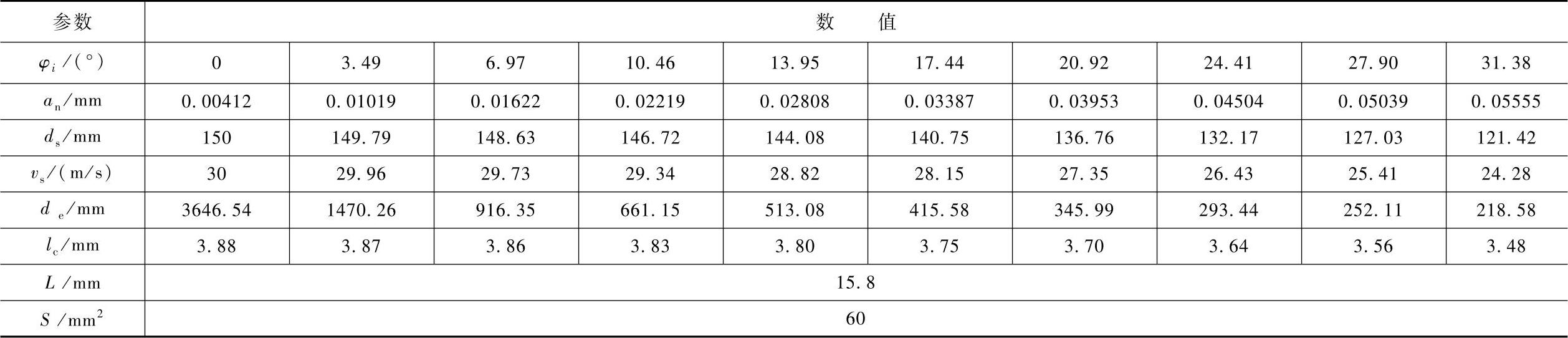
表7-10 齿轮轮廓不同位置传入工件的热比率及平均热流密度计算结果

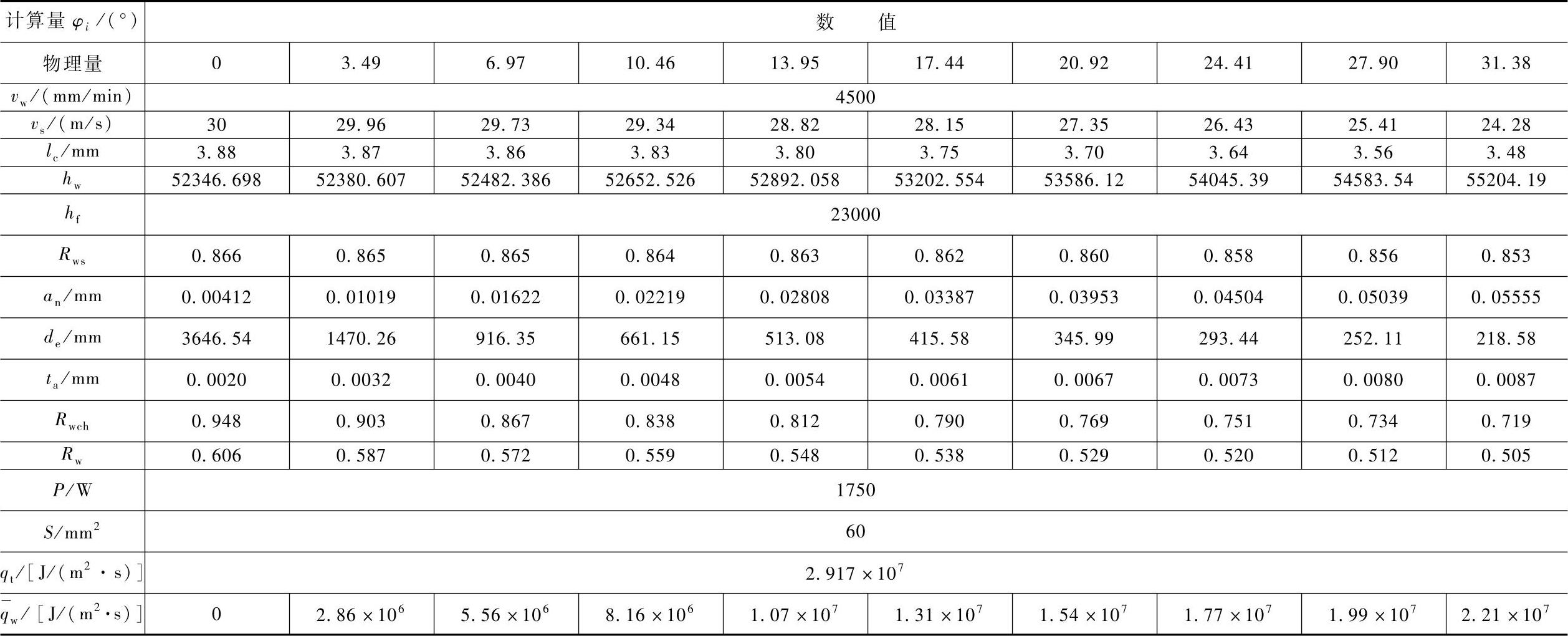
整个工件-砂轮接触面上的热流密度为：

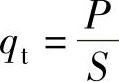
根据第5章的分析，热流密度沿渐开线非均匀分布切与滚动角存在如下关系

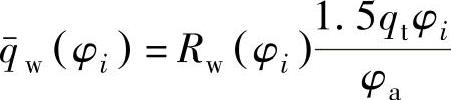
将齿轮齿廓沿渐开线按滚动角φ_i均匀分成10段，分别计算各位置传入工件的热比率及平均热流密度，计算结果见表7-10。

图7-3和图7-4分别为根据表7-10的计算结果作出的齿轮成形磨削时，传入工件的热比率和平均热流密度与齿轮轮廓渐开线滚动角的关系曲线。

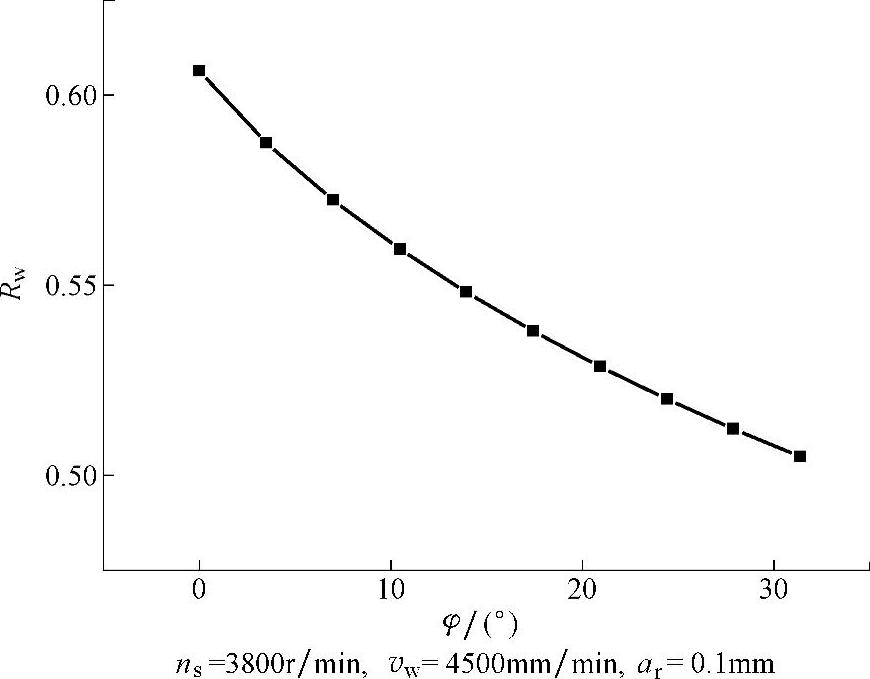
图7-3 传入工件的热比率与齿轮轮廓渐开线滚动角的关系曲线

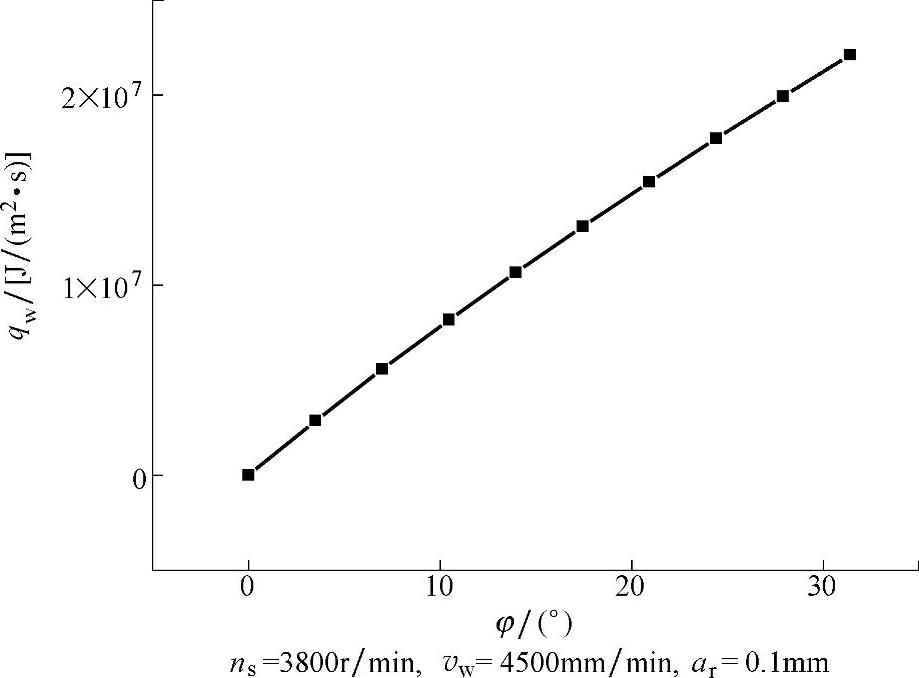
图7-4 传入工件的平均热流密度与齿轮轮廓渐开线滚动角的关系曲线