磨削温度场理论计算方法优化

根据本书2.4节的分析，平面磨削温度场可通过下式计算

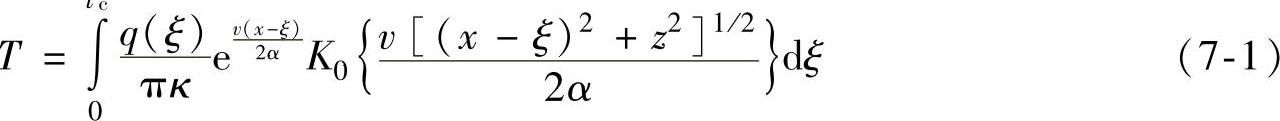
式中 K₀[u]——零阶二类修正贝塞尔函数；

q（ξ）——热源热流密度分布函数；

κ——工件材料的导热系数；

α——工件材料的热扩散系数；

v——热源移动速度；

l_c——热源与工件的接触长度。

在上述基本模型中，若假设热源为均匀分布则

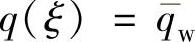
考虑到磨削区磨屑厚度从薄到厚的变化，造成磨削区磨粒上所受的力由切入处向切出处逐渐变大，若假设热源呈三角形热源分布，则

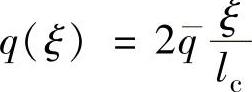
利用均匀热源模型分析，平面磨削温度场计算式如下

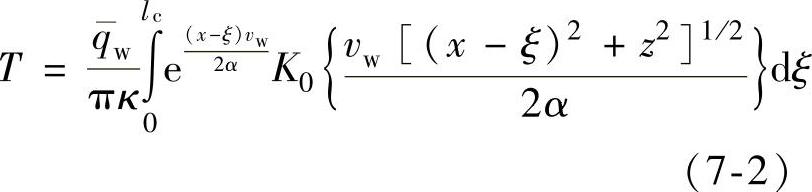
而利用三角形热源模型分析，磨削温度场计算式如下

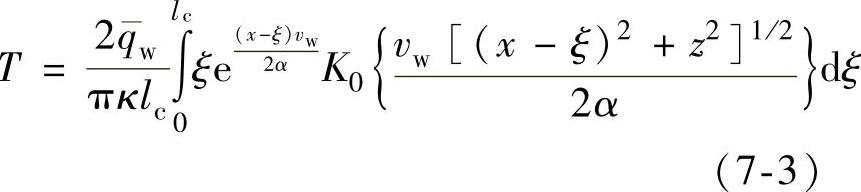
(https://www.xing528.com)

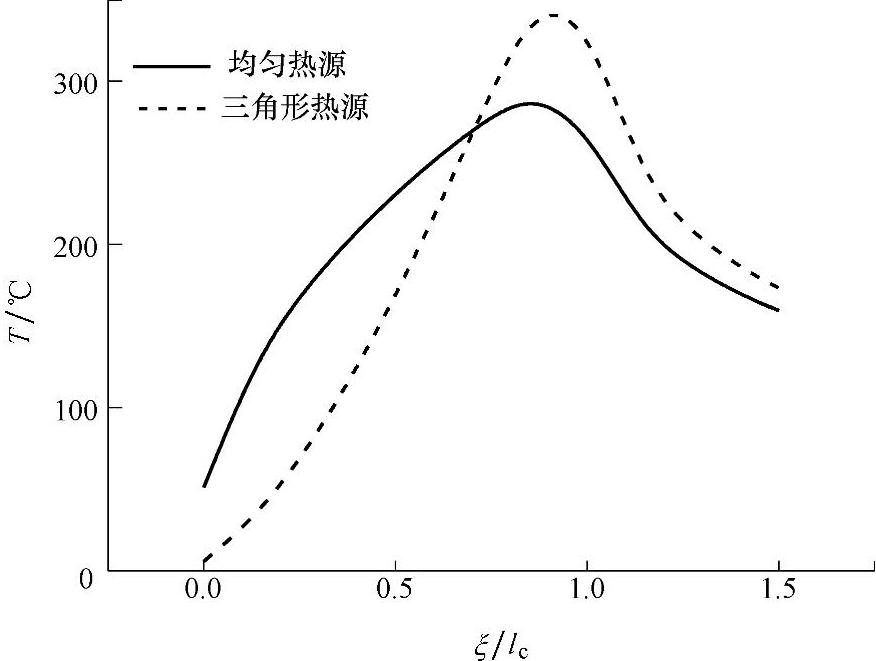
图7-1 磨削表面温度在接触弧长方向上的分布情况

对式（7-2）进行数值积分，计算得到均匀热源分布情况下，工件表面及工件不同深度各点的温升分别见表7-3和表7-4；对式（7-3）进行计算得到三角形热源分布情况下，工件表面及工件不同深度各点温升分别见表7-5和表7-6。

根据表7-3和表7-5的计算结果，得出磨削表面温度在磨削接触弧长方向的分布情况，如图7-1所示。

根据表7-4和表7-6的计算结果，得出磨削表面下不同深度的温升与距表面深度的关系曲线，如图7-2所示。

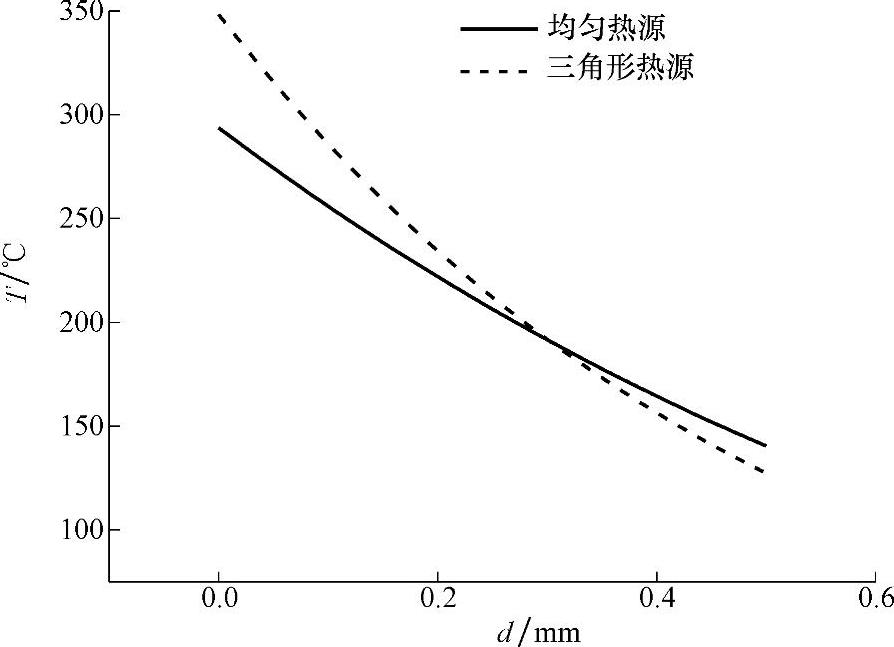
图7-2 磨削表面下不同深度的温升与距表面深度的关系曲线

表7-2 传入工件的平均热源强度计算

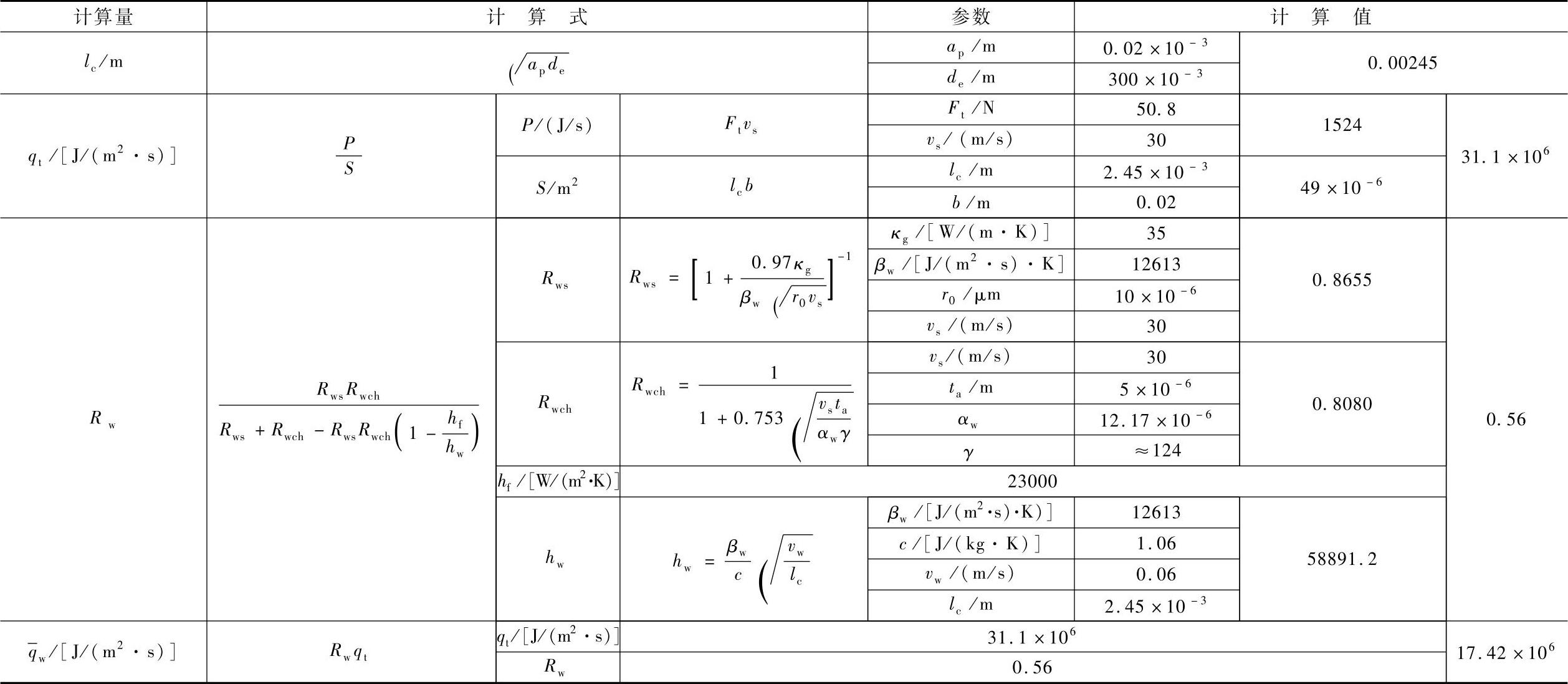
表7-3 均布热源情况下工件表面温升

表7-4 均布热源情况下工件不同深度各点温升

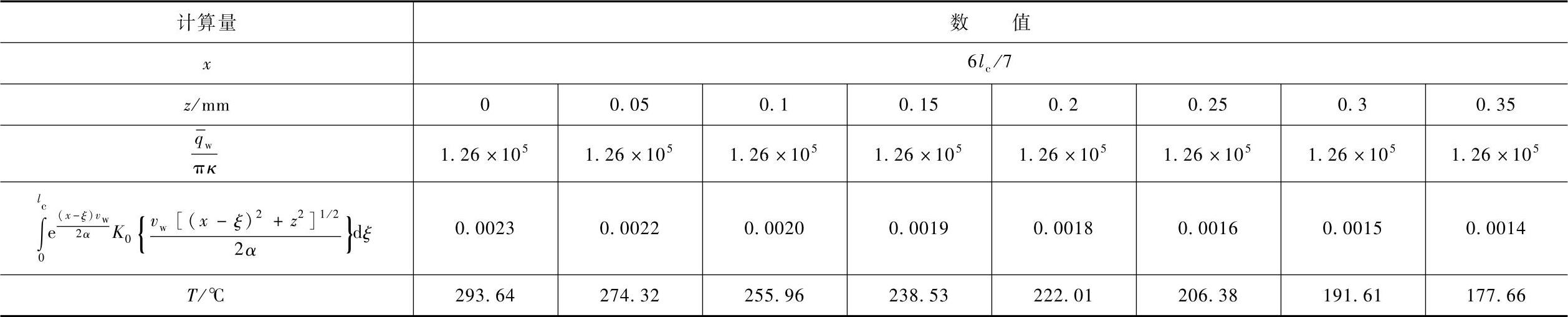
表7-5 三角形热源情况下工件表面温升

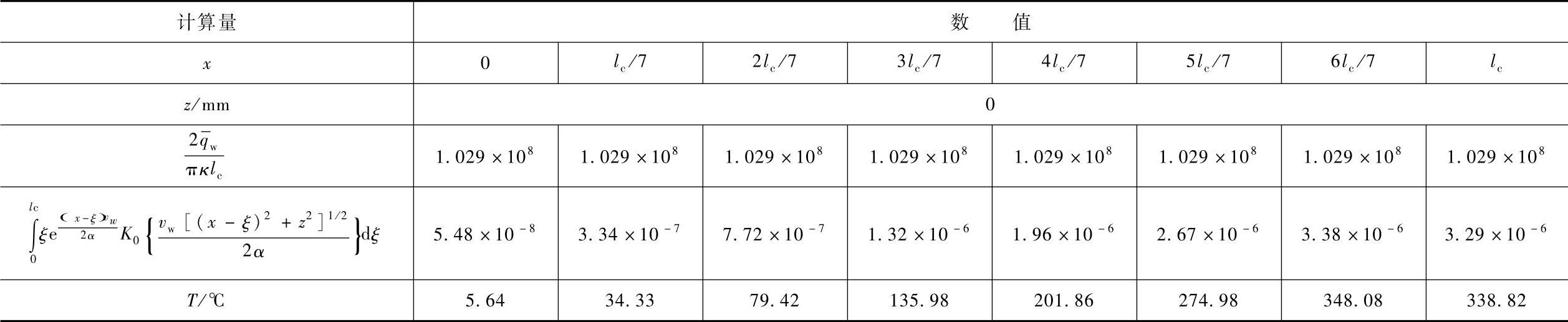
表7-6 三角形热源情况下工件不同深度各点温升