齿轮成形磨削温度场的理论计算方法

因为齿轮成形磨削中的热源是分布在渐开线形状的曲面上，因此首先分析了运动持续发热点热源温度场，然后通过对点热源沿渐开线进行积分得到了运动持续发热渐开线热源的温度场（图5-32），最后在整个齿轮—砂轮接触面上对渐开线热源进行积分获得了齿轮成形磨削的温度理论模型。

选取磨粒与齿轮表面接触任意点作为热源点O（x₀，y₀，z₀），分析该点产生的热量对磨削区中任意位置温度的影响。式（5-29）表示磨削区中任一点M（x，y，z）受磨削热源影响而产生的温度变化情况

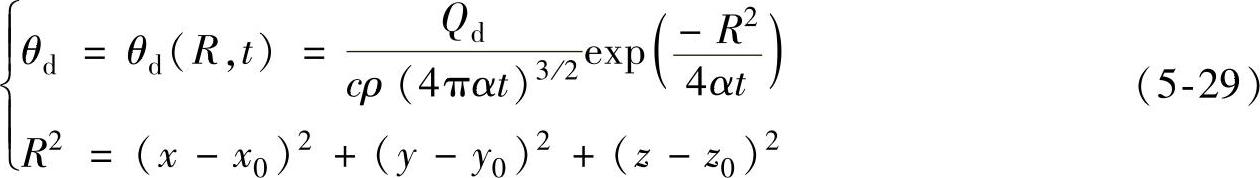
式中 θ_d——瞬时点热源引起的温升；

R——分析点到热源的距离；

Q_d——热源总热量；

c——材料比热容；

ρ——材料密度；

α——材料热扩散率。

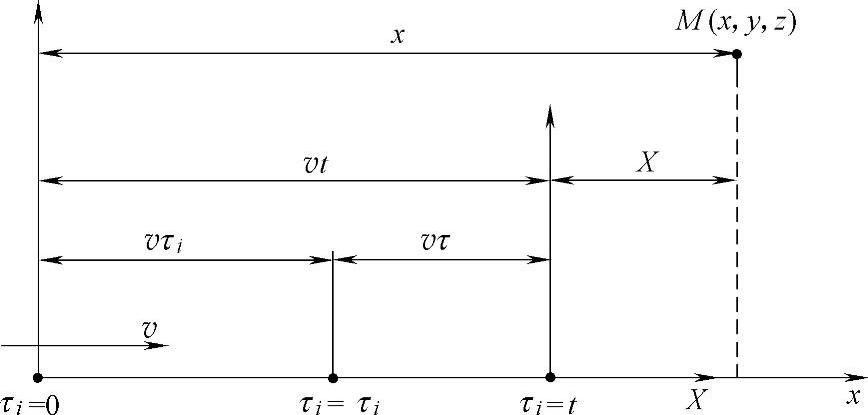
图5-32 移动点热源示意图

若热源沿着x轴匀速移动，持续移动点热源的温度场可以等效为沿着移动方向的瞬时点热源对时间的积分，取τ_i时刻的一个瞬间dτ_i进行考虑。这一瞬间的点热源发热强度为Q_ddτ_i，把这一瞬间的发热看作瞬时发热，这时刻到观察时刻t的时间间隔为τ（τ=t-τ_i）。此时发热点距离观察点之间的距离为

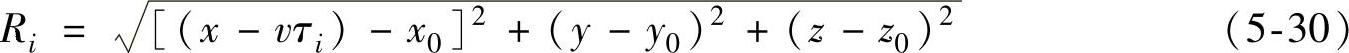
根据式（2-2），工件内任意点M（x，y，z）在观察时刻造成的温升为

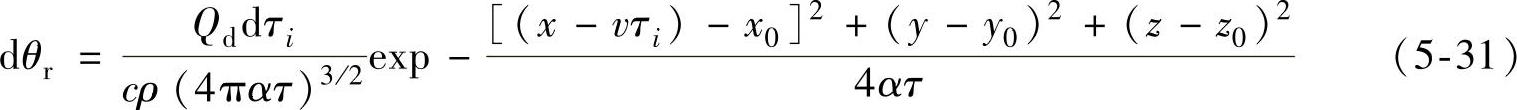
从τ_i=0到τ_i=t的整个过程中，所有瞬间的发热对M点作用所造成的总温升为

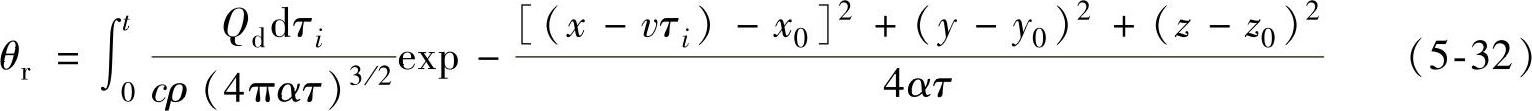
对上式进行简化处理，得到单一点热源运动持续发热造成的温度分布为

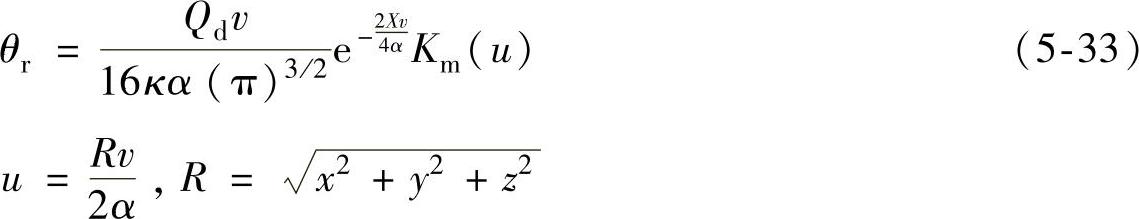
式中 κ——工件材料传导系数；

K_m（u）——特殊函数，其表达式为

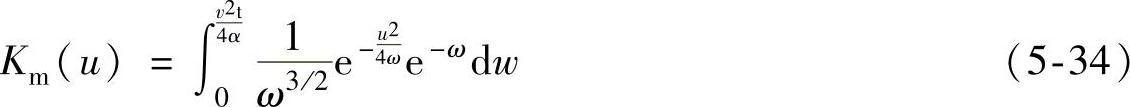
在齿轮渐开线上，坐标为（0，r_b（sinφ_i-φ_icosφ_i），r_b（cosφ_i+φ_isinφ_i））的一个微分段可以看作是一个沿着x坐标以速度v移动的点热源，如图5-33a所示。假定热流沿齿轮轮廓方向的分布与局部法向磨削深度的分布一致。根据第5.1.1节的分析结果，渐开线上任意微分段的热源强度为q_l（φ_i）d_l，且存在如下关系

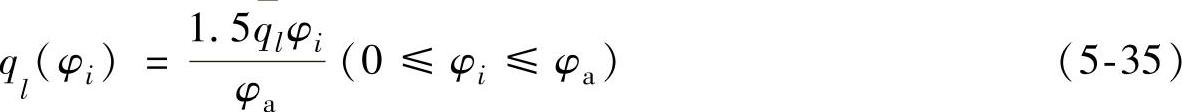
dl=r_bφ_idφ_i （5-36）

根据式（5-33），由该微分段热源引起的工件内任意点M的温升可由下式表示

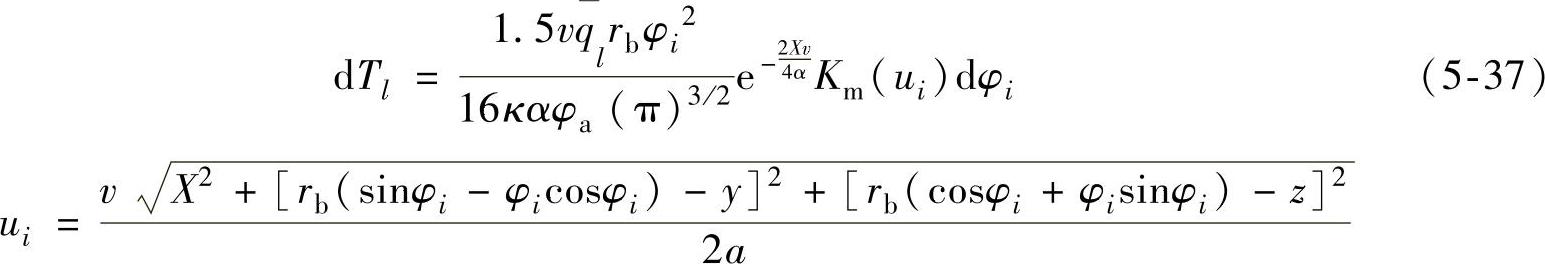
式中 q_l——该渐开线上的平均热流密度；

v——工件速度；

r_b——基圆半径；(www.xing528.com)

φ_i——任意位置的滚动角；

φ_a——齿顶位置的滚动角。

对式（5-37）沿渐开线积分，可以得到工件内任意点受该有限长、运动持续非均匀发热渐开线热源q_l（φ_i）影响引起的温升如下

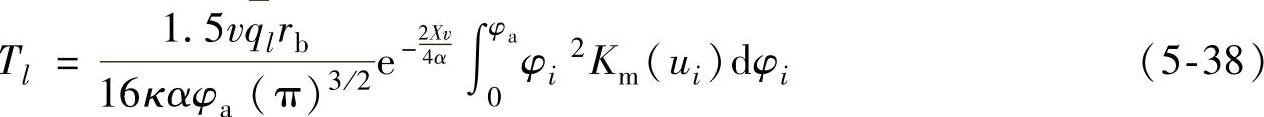
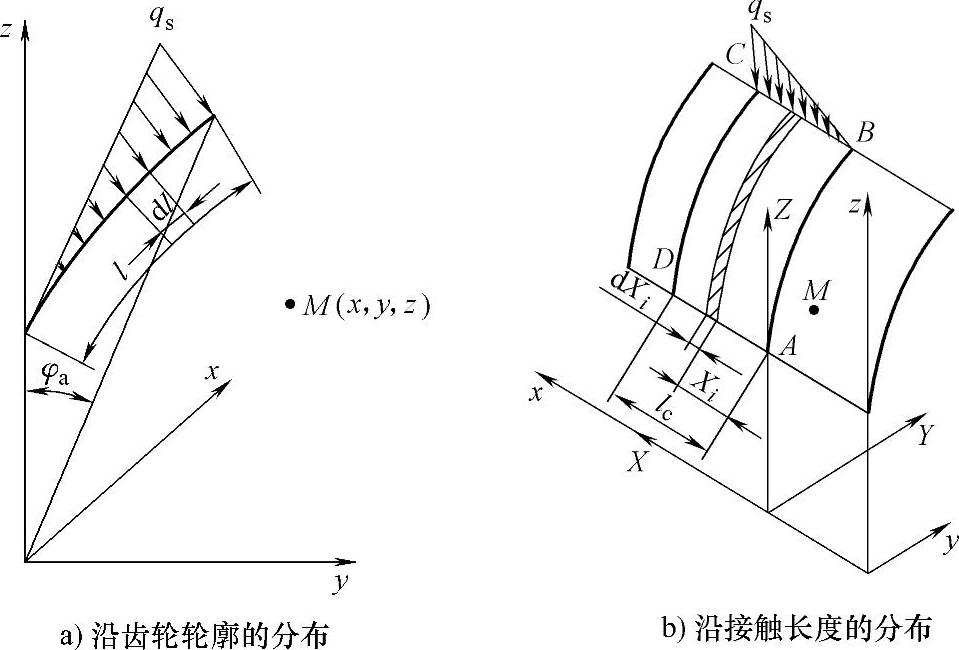
图5-33 热流密度在齿轮—砂轮3D接触表面的分布

如图5-33b所示，齿轮—砂轮的三维接触区磨削接触ABCD是由无数条渐开线或微分宽度为dX_i的渐开线窄条组成。根据式（5-31），X_i处的渐开线热源对点M（x，y，z）造成的温升可由下式表示

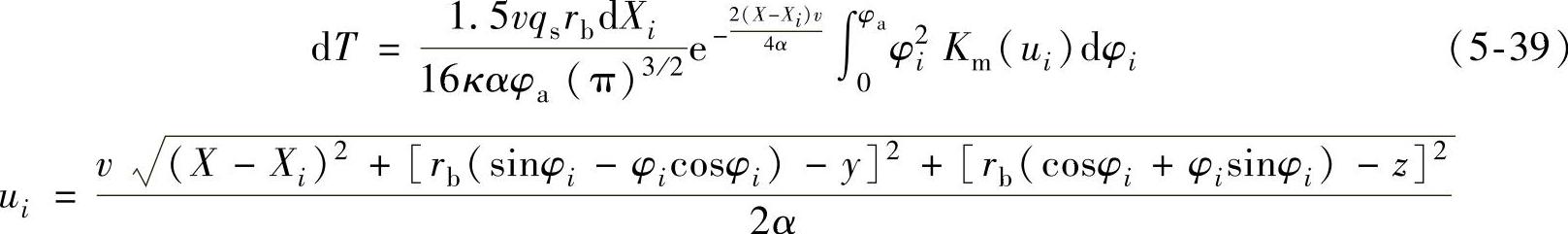
假设热流在磨削接触弧上呈三角形分布^[6-8]，，。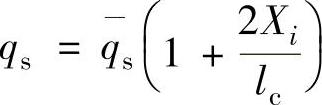

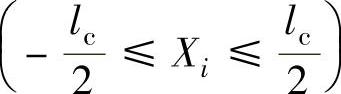对式（5-39）沿接触弧长积分，可得到受有限大移动非均匀渐开面热源热流密度分布为q_s（φ_i，X_i）的作用，任意点M（x，y，z）产生的温升为

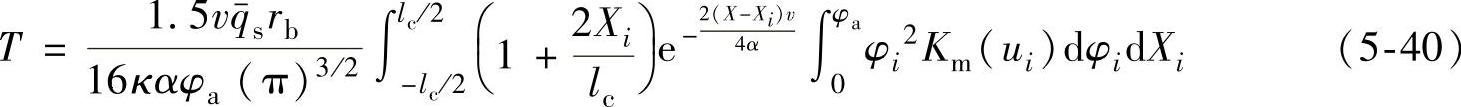
式中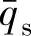——接触面的平均热流密度；

l_c——工件—砂轮接触弧长。

式（5-40）是基于工件在x，y，z三个方向无限大而推导出来的，但在实际齿轮成形磨削时，齿轮的轮齿高度和齿轮的宽度通常都远大于工件—砂轮的接触弧长。因此，沿齿宽方向和渐开线延伸方向的热传导可以假设是在无限大导热体内传导，但由于齿轮表面绝热的作用，沿垂直于齿面的方向，热传导只能在半无限大导热体的体内发生^[9]。式（5-40）中的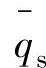理论上是原有数值的两倍，因此式（5-40）应改为

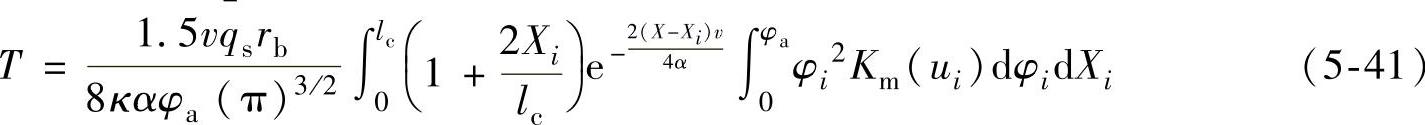
上式即齿轮成形磨削温度场理论模型。式（5-41）可转换为无量纲形式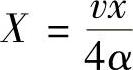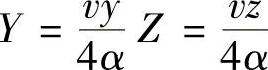，，帕克莱数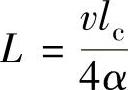，无量纲温升为

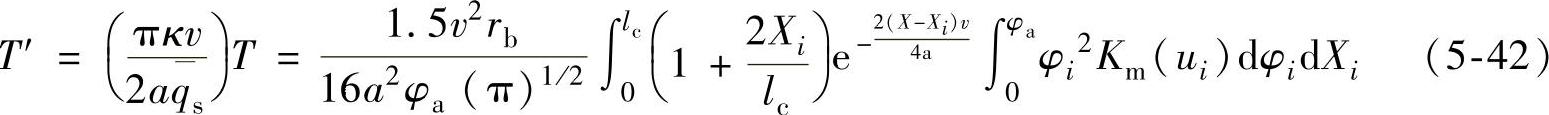
利用式（5-42）计算出不同帕克莱数条件下磨削齿轮模数为8、齿数为28的直齿轮，齿轮—砂轮接触表面的无量纲温度分布如图（5-34）所示。其中，图5-34a所示为分度圆位置无量纲温度沿接触弧的分布；图5-34b所示为接触弧中部（X/l_c=0）无量纲温度沿齿轮轮廓的分布。可见，高的帕克莱数将增加齿轮轮廓表面的温度，并且沿齿轮轮廓线方向，磨削温度从齿根至齿顶逐渐增大。

砂轮—齿轮接触表面及齿轮内部无量纲温度分布如图5-35所示。

不同模数情况下接触面的无量纲温度分布见图5-36，可见齿轮模数并不影响接触面的温度分布。

齿轮齿数不同时接触面无量纲温度分布如图5-37所示，随着齿轮齿数的增加，磨削温度也随之升高。

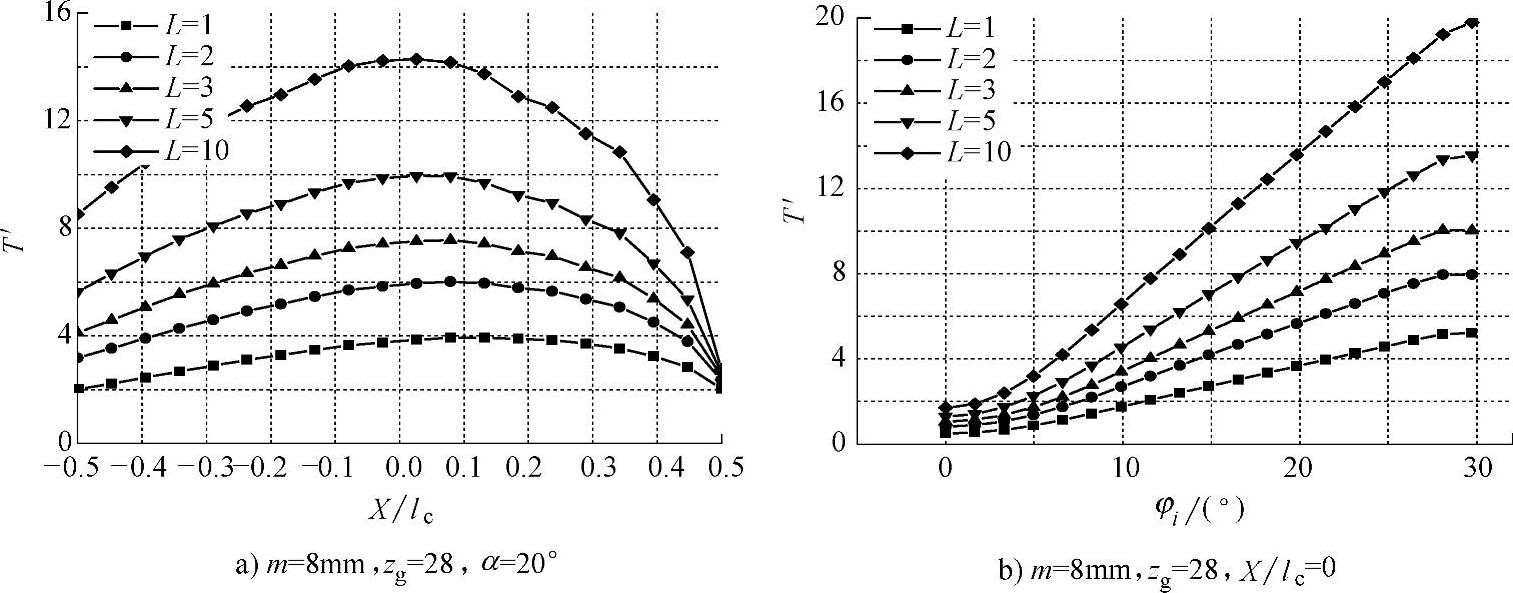
图5-34 齿轮—砂轮接触面上无量纲温度的分布

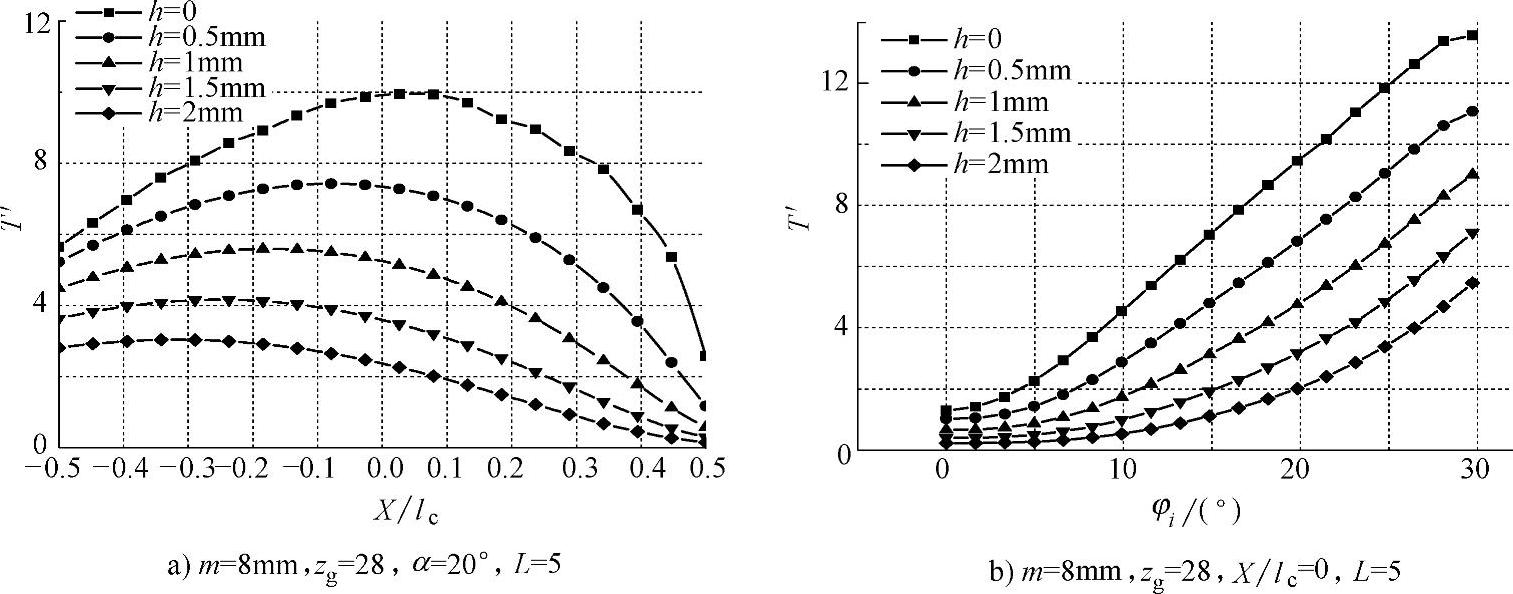
图5-35 接触表面及齿轮内部无量纲温度分布

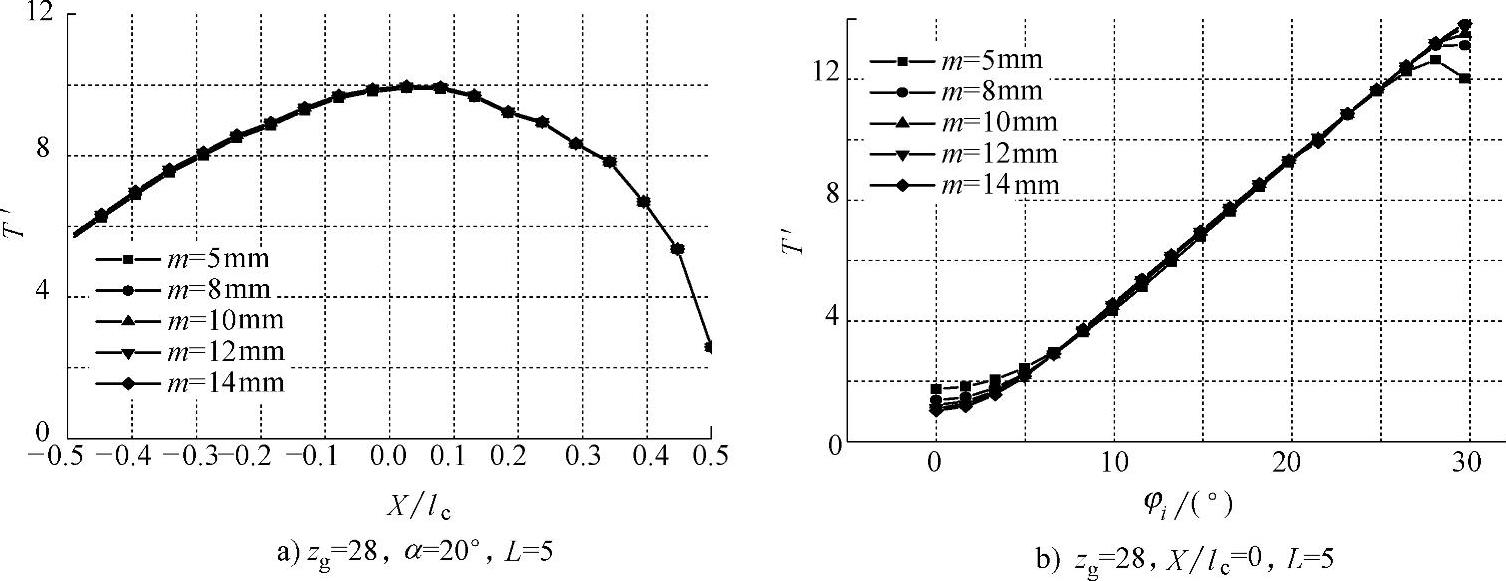
图5-36 不同模数情况下接触面的无量纲温度分布

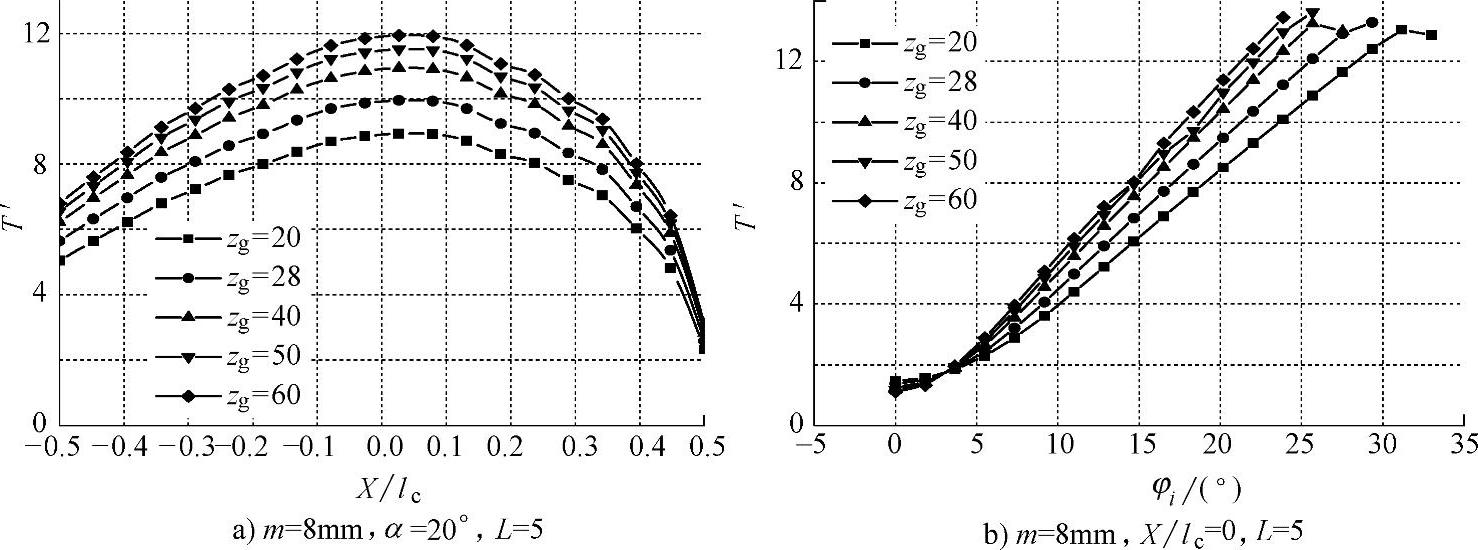
图5-37 不同齿数情况下接触面的温度分布