瞬时有限长均匀渐开线热源与非均匀渐开线热源的温度场分析

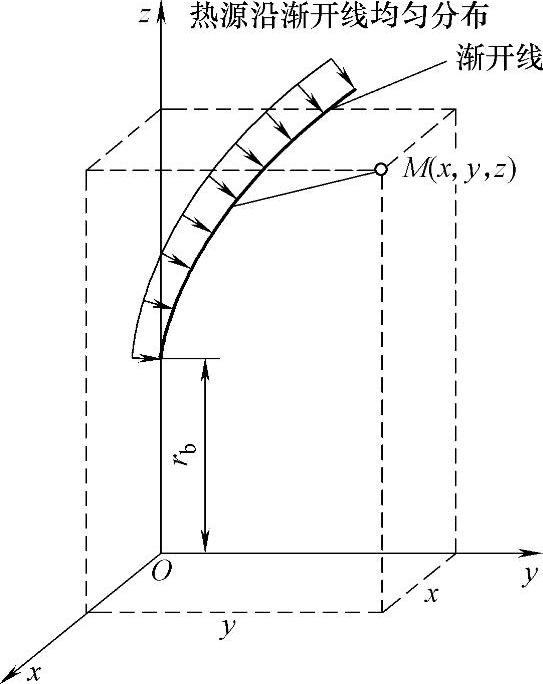
图5-24 瞬时有限长均匀渐 开线热源示意图

成形磨削与平面磨削最大的区别在于工件—砂轮接触线不同，在运用平面磨削温度理论计算时，可以通过对点热源沿直线从负无穷大到正无穷大积分，得到线热源温度场；而成形磨削时，则需要对点热源沿成形轮廓曲线从起始点到终点积分，得到曲线热源温度场。

若在无限大导热体内有图5-24所示均匀分布的渐开线热源瞬时发热，已知渐开线的参数方程为

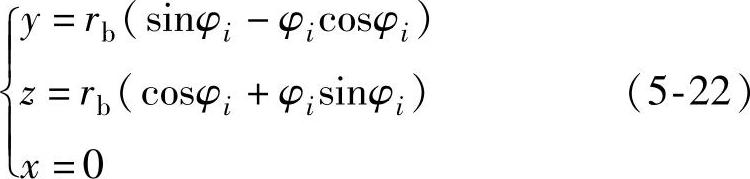
式中 r_b——渐开线基圆半径；

φ_i——渐开线任意位置滚动角。

则该导热体内任一点的温度分布可通过以下过程计算。

将渐开线分成若干微分段，任意微分段瞬时的发热强度为Q_sds。由式（5-18）可知，d_s=r_bφ_idφ_i，因此渐开线内任意点M（x，y，z）受该微分段热源影响而产生的温升。根据瞬时点热源发热温度计算，有

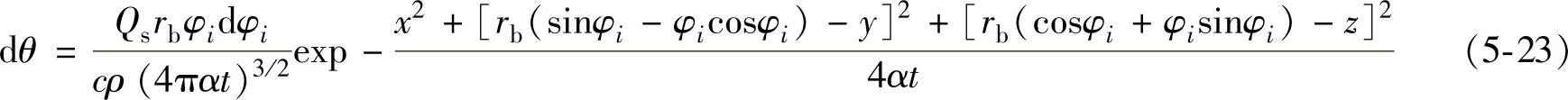
对式（5-23）沿φ_i积分得

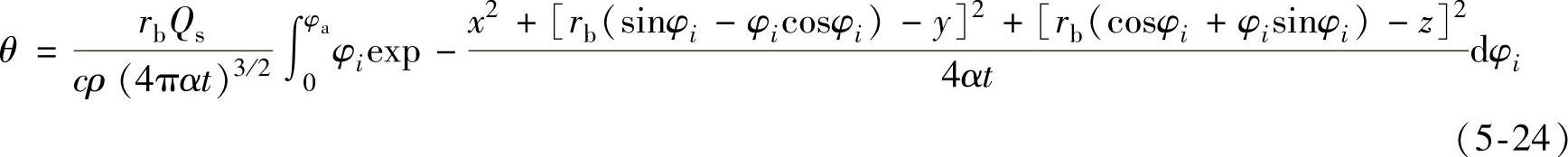(www.xing528.com)

式中 φ_a——渐开线顶端的滚动角。

若无限大导热体内渐开线上热源如图5-25所示，呈非均匀分布，且平均热流密度为Q_s，通过第5.1.2节的分析可知，在齿轮成形磨削时，齿轮轮廓上局部法向磨削深度与轮廓渐开线滚动角之间存在线性关系。因此，假设渐开线上的非均匀热流是渐开线滚动角的正比例函数，且存在如下关系^[4，5]

将渐开线分成若干微分段，任意微分段瞬时的发热强度为Q_s（φ_i）ds，则该导热体内任意点的温度分布可通过以下过程计算

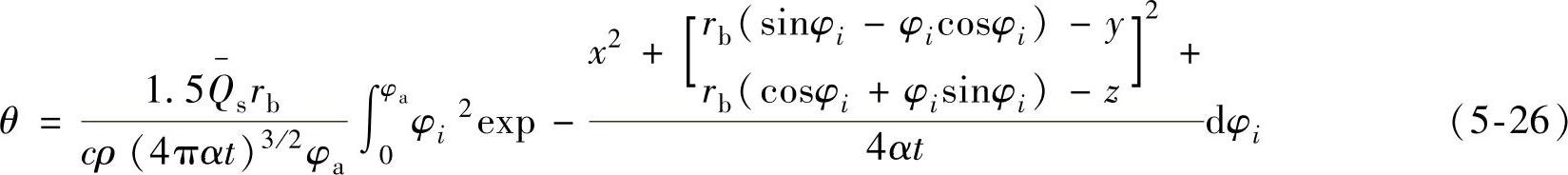
为对比两个热源的温度场，设t=0.05s，r_b=200mm，φ_a=35°，且忽略式（5-25）和式（5-26）中的常数项，对两式进行数值积分，可得到x=0位置渐开线内部等效温度场的分布分别如图5-26和图5-27所示。

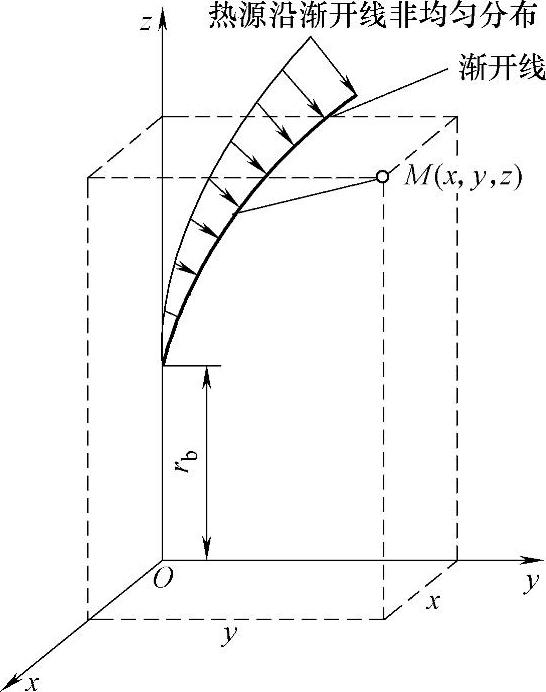
图5-25 瞬时有限长非均匀渐开线热源示意图

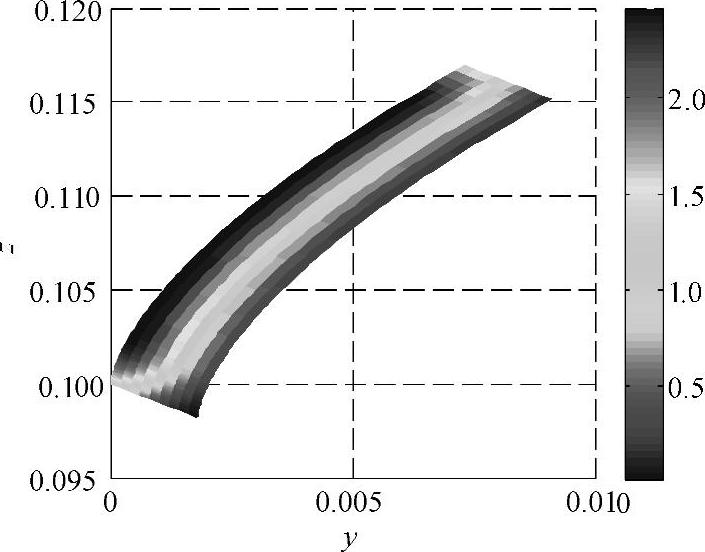
图5-26 瞬时有限长均匀渐开线热源温度场

两个温度场的区别同样非常明显，联系到第5.1.2节的分析结果，齿轮成形磨削，轮廓线上任一点的法向磨削深度随滚动角增加而增大，且基本呈线性变化，因此第二种热流分布情况更符合齿轮成形磨削的实际情况。