【摘要】:在初始时刻t=0的一瞬间,随后立即停止发热,则该导热体中任意位置的温度分布可由下式计算图5-20 瞬时有限长均匀线热源示意图图5-21 瞬时有限长非均匀线热源示意图为对比两个热源的温度场,设t=0.05s,Lg=15mm,且忽略两式中的常数项,根据式和式计算得到瞬时有限长均匀线热源的等效温度场和瞬时有限长非均匀线热源的等效温度场,如图5-22和图5-23所示。
在无限大的导热体内有一条有限长的线热源,如图5-20所示。在初始时刻t=0的一瞬间,全线均匀地发出一股热量Qs,随后立即停止发热,该导热体中任意位置的温度分布可由下式计算[3]。
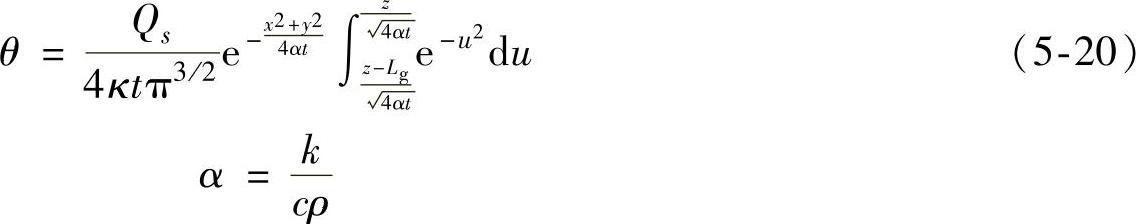
式中 κ——导热系数;
α——热扩散系数;
c——比热容;
ρ——密度;
Lg——热源长度;
x、y、z——空间坐标。
若无限大的导热体内,有限长的线热源为非均匀分布,线热源的平均热流密度为 ,如图5-21所示。在初始时刻t=0的一瞬间,随后立即停止发热,则该导热体中任意位置的温度分布可由下式计算
,如图5-21所示。在初始时刻t=0的一瞬间,随后立即停止发热,则该导热体中任意位置的温度分布可由下式计算
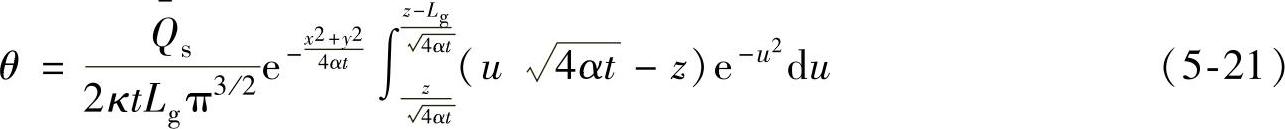
 (https://www.xing528.com)
(https://www.xing528.com)
图5-20 瞬时有限长均匀线热源示意图
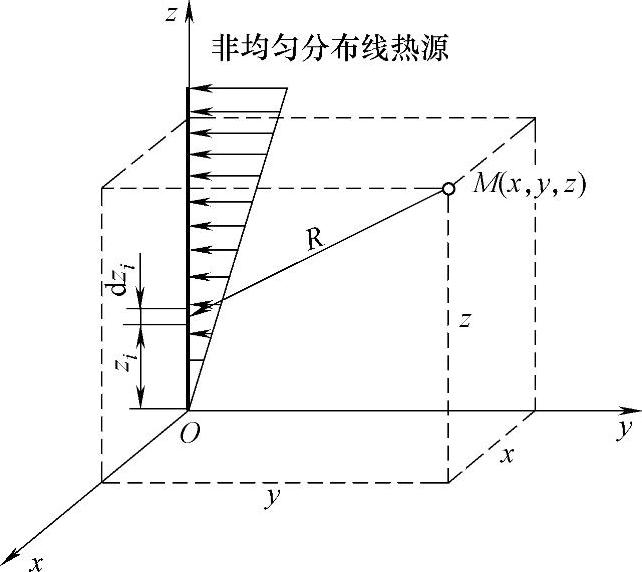
图5-21 瞬时有限长非均匀线热源示意图
为对比两个热源的温度场,设t=0.05s,Lg=15mm,且忽略两式中的常数项,根据式(5-20)和式(5-21)计算得到瞬时有限长均匀线热源的等效温度场和瞬时有限长非均匀线热源的等效温度场,如图5-22和图5-23所示。
两个温度场区别非常明显。瞬时有限长均匀线热源的温度场在长度方向分布均匀,与瞬时无限长均匀线热源的温度场分布极其相似。通常用瞬时无限长均匀线热源的温度场代替,这也是在平面磨削温度场理论计算中,通常将磨削接触面假设成由平行于砂轮宽度的无数条无限长线热源的依据。而瞬时有限长非均匀线热源的温度场在长度方向分布不均匀,在长度方向沿热流密度增大的方向温度也随之增高。因此,若磨削过程中,沿砂轮宽度方向的热流密度分布不均,则现有的磨削温度理论模型将不再适用。

图5-22 瞬时有限长均匀线热源温度场
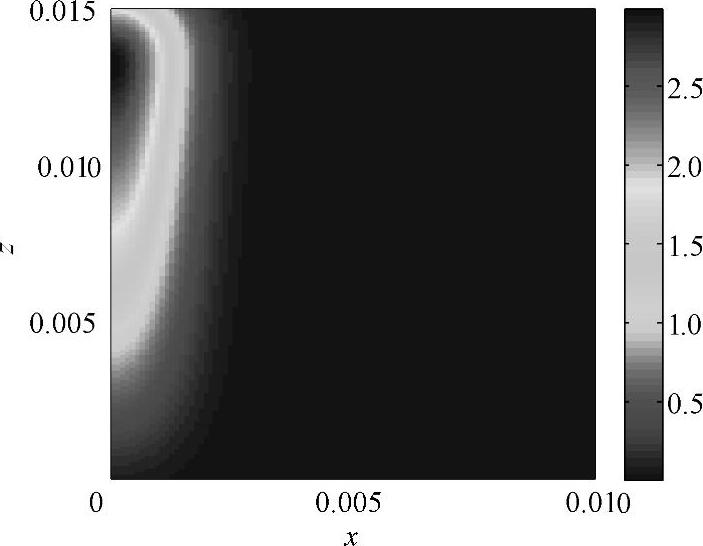
图5-23 瞬时有限长非均匀线热源温度场
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




