如何优化局部法向磨削的深度？

在齿轮成形磨削时，砂轮被修整成齿轮齿槽的形状，磨削的加工参数包括砂轮转速n_s、工作台速度v_w和径向进给深度a_r。径向进给深度是在齿轮成形磨削时，砂轮沿砂轮中心和齿轮中心连线方向进给的深度，由于齿轮轮廓表面是曲面，因此表面上不同位置的法向磨削深度（沿轮廓面曲线曲率半径方向的进给深度）各不相同，如图5-2所示。

局部法向磨削深度与径向进给深度的关系如图5-3所示。

图5-3中a_r为成形砂轮径向进给深度；a_n（φ_i）为齿轮渐开线轮廓上任意位置的局部法向磨削深度；θ_i为展角；α_i为压力角；φ_i为滚动角；β为基圆齿距对应的圆心角的一半，β与齿轮的齿数有关；γ（φ_i）为齿轮轮廓上任意点的曲率半径与砂轮中心和齿轮中心连线的夹角。

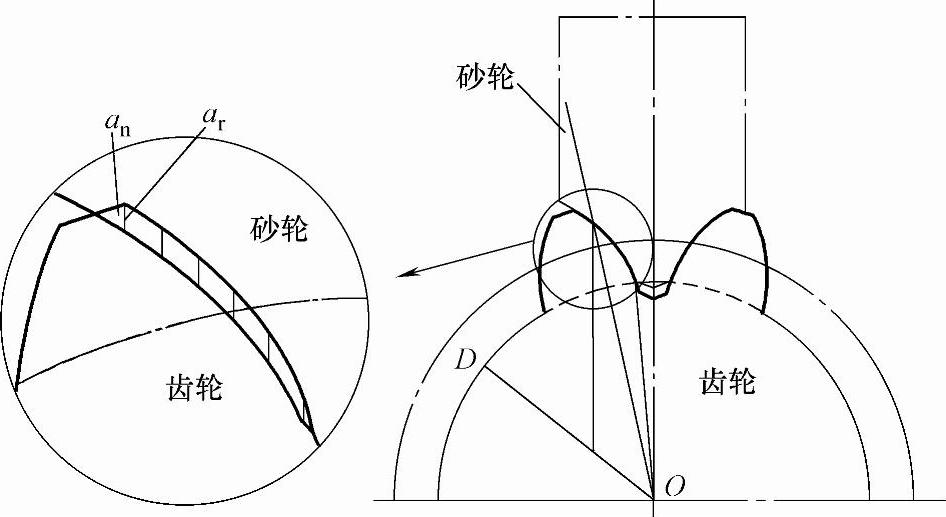
图5-2 法向磨削深度

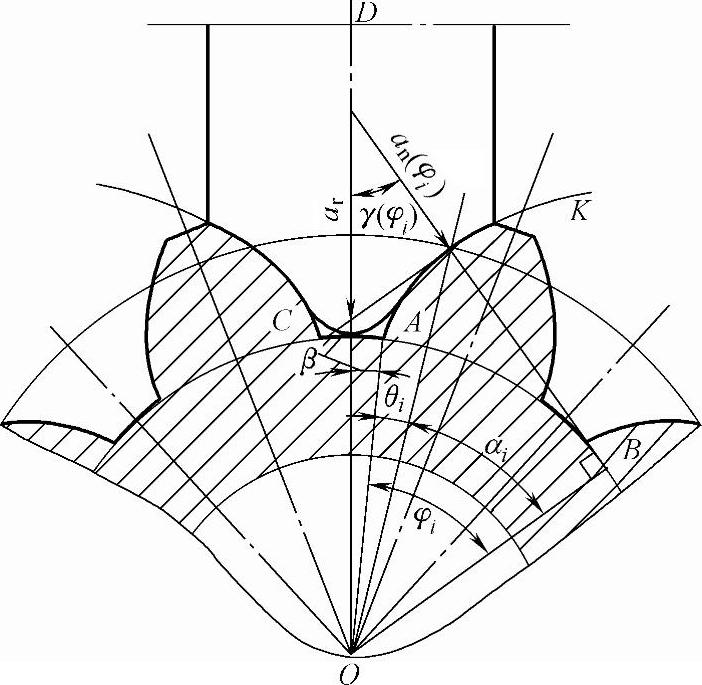
图5-3 局部法向磨削深度与径向进给深度的关系

因此有如下关系^[1]

a_n（φ_i）=a_r cos（γ（φ_i）） （5-5）(www.xing528.com)

式中 e_b——基圆齿距。

通过式（5-5）计算得到不同径向进给深度a_r条件下，局部法向磨削深度a_n沿齿轮轮廓渐开线随渐开线滚动角φ_i的变化，如图5-4所示；在相同a_r条件下，齿轮齿数z_g对局部法向磨削深度a_n变化的影响，如图5-5所示。

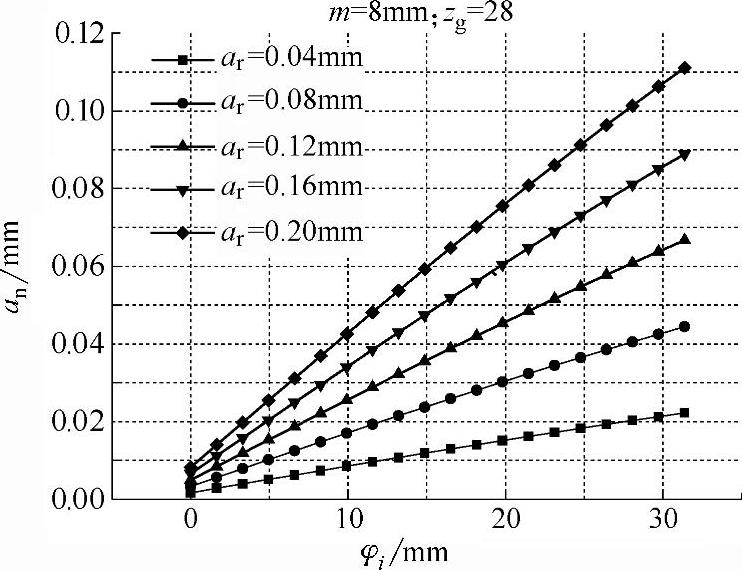
图5-4 不同a_r情况下a_n随φ_i的变化

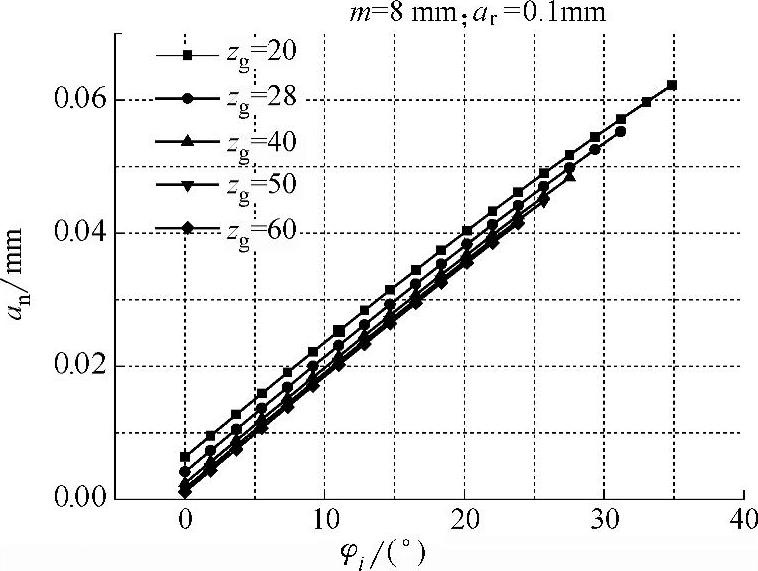
图5-5 相同a_r情况下z_g对a_n的影响

从图5-4和图5-5看出，均布法向磨削深度a_n随齿轮轮廓渐开线滚动角的增大而增大，且基本呈线性关系，即齿根处的磨削深度较小，齿顶处的磨削深度最大；齿轮的几何形状也影响局部磨削深度的分布，对于模数相同的齿轮，齿数越少，则局部磨削深度越大；齿轮模数几乎不改变局部磨削深度的分布。