磨削区流体模型计算结果分析

图4-5、图4-6和图4-7所示为典型的计算结果，包括磨削区内流体压力、流体在砂轮表面渗入深度以及流体切向速度。假设砂轮与工件之间的间隙H₀为与砂轮表面磨粒突出高度具有相同量级，具体取值为砂轮磨粒直径的1/2。计算中采用的磨削液热特性与运动特性见表4-2。

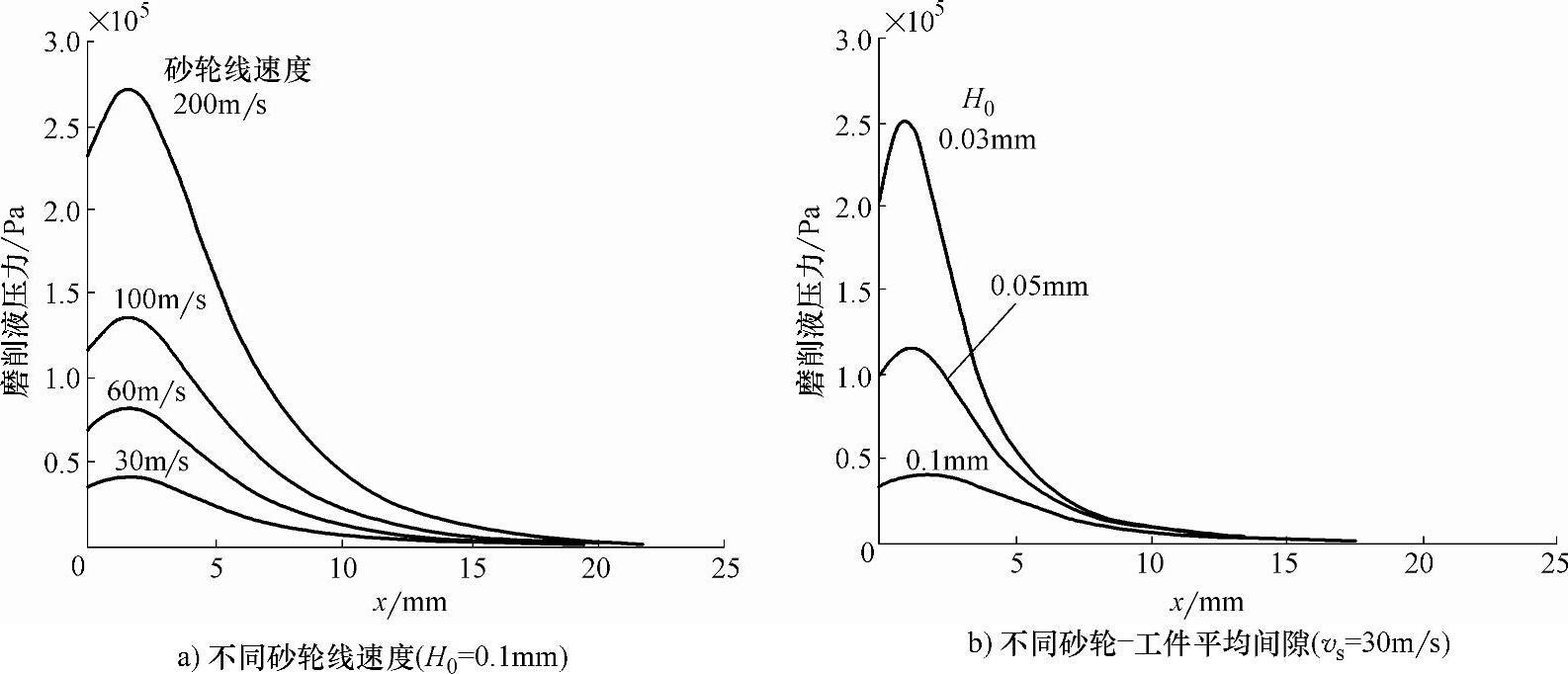
图4-5 磨削液入口处压力分布（水基磨削液，室温，v₀=0.6m/s，R=125mm）

表4-2 磨削液热特性与运动特性

图4-7a的计算结果表明，在交点E处（见图4-4）的流体渗入砂轮深度与磨削速度密切相关，该数值直接影响磨削区内的流体厚度。由于流体动压效应的影响，流体渗入砂轮表面的深度显著提高，如图4-7b所示。如果考虑流体侧向泄漏的影响，磨削液入口处的实际压力可能会比图4-5的计算结果要低。图4-7中流体渗入砂轮深度的上限，是砂轮与工件之间的磨削间隙H₀，其包含了砂轮表面气孔率的影响。对于平均磨粒直径为d=0.2mm的情况，该间隙大约为H₀≈d/2≈0.1mm（对于表面气孔率较大的砂轮，该间隙值也会有所提高）。因此，对于砂轮速度在100m/s以下的情况，磨削区内流体厚度可以达到0.1mm。

图4-6 砂轮表面流体切向速度（水基磨削液，室温，v₀=0.6m/s，φ=0.4，β₁=1.75，α₁=150，d=0.2mm）

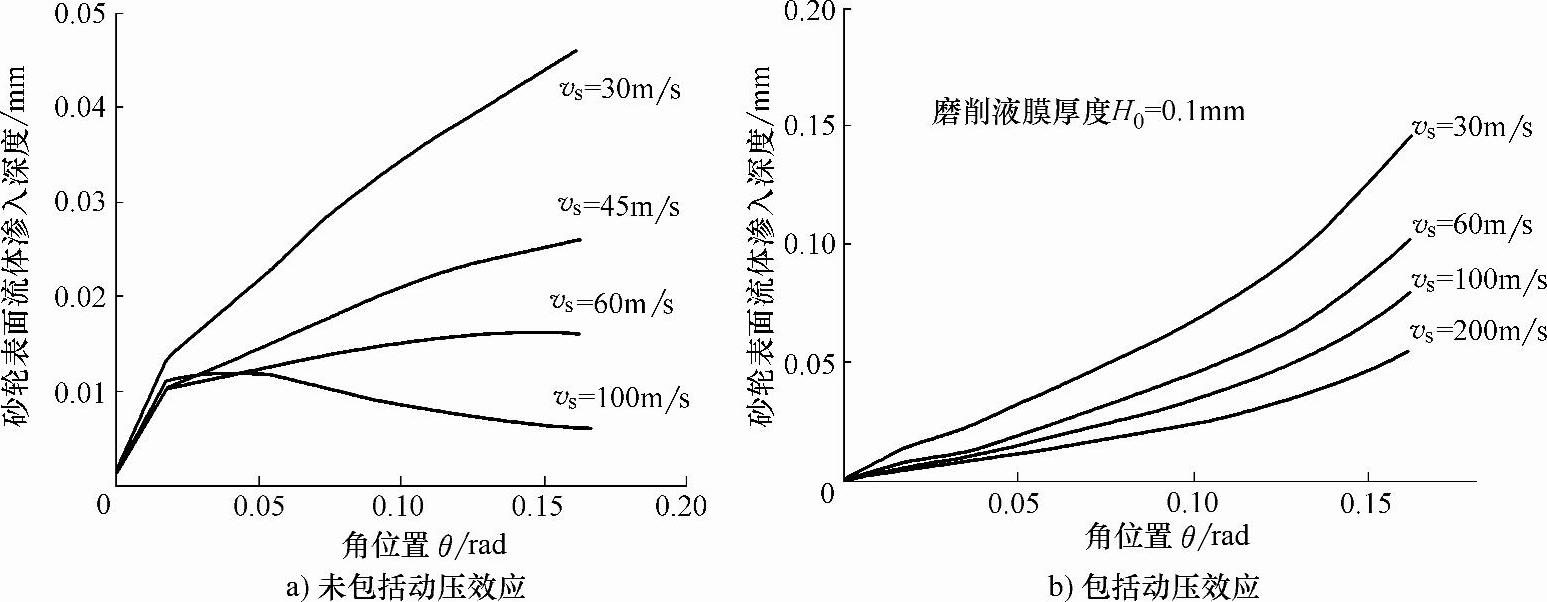
图4-7 砂轮表面流体渗入深度（水基磨削液，室温，v₀=0.6m/s， φ=0.4，β₁=1.75，α₁=150，d=0.2mm，H₀=0.1mm）

采用Engineer等人对磨削液有效流量的测量数据[9]，可根据式（4-11）对磨削区内砂轮表面的薄层流体厚度进行估算。对于磨削液入口速度为0.61m/s（磨削液供给流量为70mL/s，喷嘴截面面积为113mm²）、砂轮速度为30m/s的情况，在砂轮表面有效气孔率φ=0.4～0.9时，流体厚度在0.01～0.03mm之间变化。由于砂轮表面有效气孔率的不同，实际测量获得的磨削液利用率在0.05～0.17之间变化。按此方法估算得到的磨削区内水基磨削液的厚度，在不包括流体动压效应时，与图4-7中模型预测的结果在数量级上比较接近。在其他试验条件不变的情况下，将喷嘴移近磨削区，所用砂轮为普通刚玉砂轮（38A60K5VBE，φ=0.4），测得的磨削液利用率达到0.33，估算得到的磨削液的厚度达到0.062mm（喷嘴流量仍为70mL/s）。上述估算结果显示，在流体供给速度相对较低时，流体动压效应的影响不是很显著；对于缓进给磨削和高速高效深切磨削（HEDG）的情况，由于磨削液供给速度和压力较大，流体动压效应的影响应该会变得显著。Tsunasawa等人通过监控薄层流体的电阻值，实际测量了磨削接触区的流体厚度。他们的测量结果显示，采用传统磨削液供给方法和普通刚玉砂轮（WA60JV），在较低供给流量17～100mL/s条件下，水基磨削液在磨削区内的厚度达到0.05～0.15mm^[10]。他们采用的具体喷嘴截面尺寸没有说明，因而他们的数据还不能直接与Engineer等人的数据相比较，但他们的试验结果表明，对于F60～F70的砂轮，即使在很低的磨削液供给流量下，也可以达到流体厚度的上限值H₀≈0.1mm。对于缓进给磨削和高速高效深切磨削的情况，磨削液流量要高得多，一般在300mL/s，对于一个截面积为20mm²的典型喷嘴，磨削液供给速度可达15m/s，磨削区内的流体厚度可以很容易达到0.1mm，如图4-8、图4-9所示。(www.xing528.com)

图4-8 砂轮表面流体渗入深度（矿物油，室温，v₀=0.6m/s，φ=0.4，β₁=1.75，α₁=150，d=0.2mm，H₀=0.1mm）

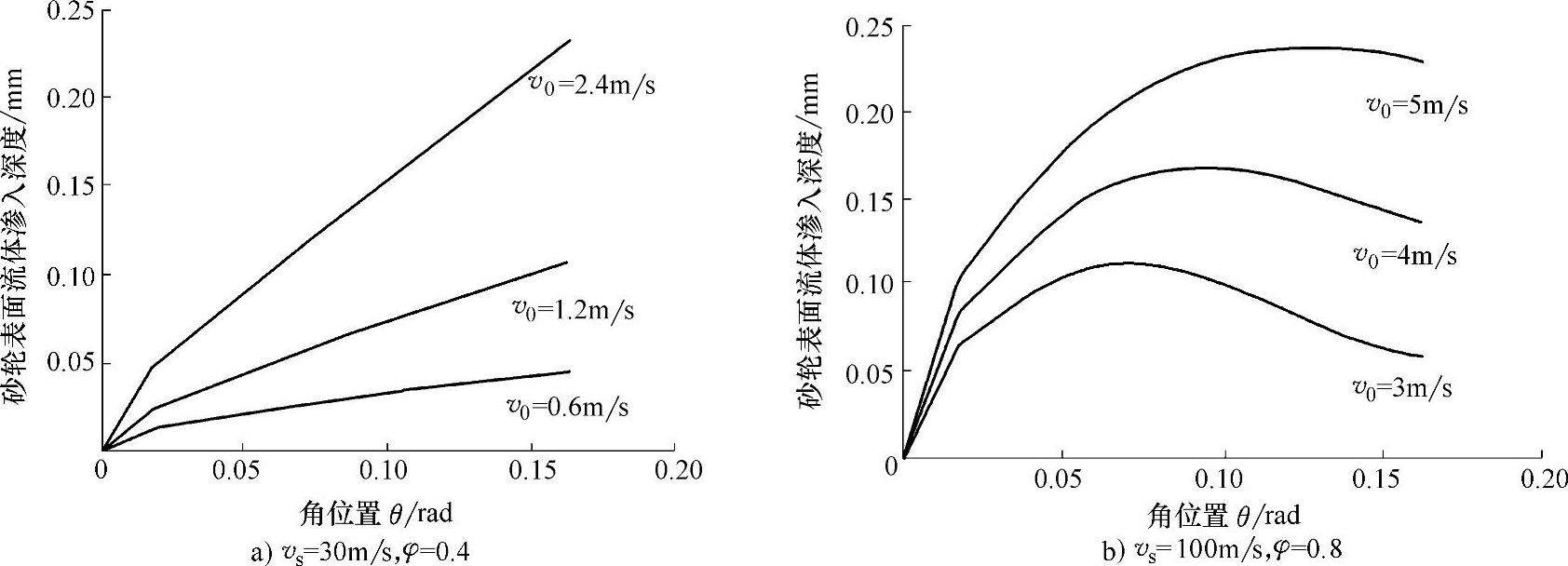
图4-9 砂轮表面流体渗入深度（矿物油，室温，不包括流体动压效应，β₁=1.75，α₁=150，d=0.2mm）

由于油基磨削液的黏度较大，动压效应对流体厚度的影响要比水基磨削液显著得多（见图4-8b）。在砂轮线速度为30～200m/s时，流体厚度最大值可达到0.3～0.7mm，但由于砂轮与工件表面最大间隙H₀的限制，流体厚度最大也不会超过0.1mm水平。如果忽略流体动压效应的影响，油基磨削液进入磨削区的流体厚度与水基磨削液相当（图4-8a）。图4-9的计算结果显示，即使不考虑流体动压效应，提高磨削液的供给速度可进一步加大渗入砂轮表面的流体厚度，对于水基磨削液，也存在类似的趋势。

式（4-19）在计算砂轮与工件之间的动压力时，忽略了砂轮表面孔隙的影响，对于树脂结合剂、金属结合剂以及电镀砂轮，这一假设基本合理。对于表面具有较大孔隙的砂轮来说，特别是在使用较低黏度的磨削液（水基磨削液）时，流体动压效应可以忽略，对于表面相对平滑的砂轮，流体动压效应可能由于磨削液侧向泄漏的影响而有所减弱。

为了进一步计算和预测磨削区内流体的表面传热系数h_c，对于磨粒粒度号为F60～F70的砂轮，在磨削液供给压力和流量较大的情况下（包括缓进给磨削和高效深切磨削的情况），取磨削区内流体厚度为0.15mm；而对于磨削液供给压力和流量较小的情况，即传统浅磨的情况，取磨削区内流体厚度在0.05～0.1mm。图4-10所示为根据式（4-1）、式（4-5）以及式（4-15）求得的磨削液表面传热系数的变化。需要指出的一点是，文献[14，15]中表面传热系数计算数值与本书图4-10不同（原数值偏高），经过详细检查，是文献中对流体动压效应数值计算有误，本书对此进行了改正。工件表面温度T_w在从室温升高到磨削液沸腾温度时，对计算结果影响较小。改变式（4-12）计算得出的磨削区内压力梯度dp/dx值，使其从计算得出的原值的10%变化至100%时，对于图4-10所示的磨削速度范围，所得表面传热系数预测值的变化小于20%。影响磨削区表面传热系数的主要因素包括砂轮速度、流体厚度以及磨削液种类。在下一节，将进一步将理论预测值与相关试验数据进行比较。

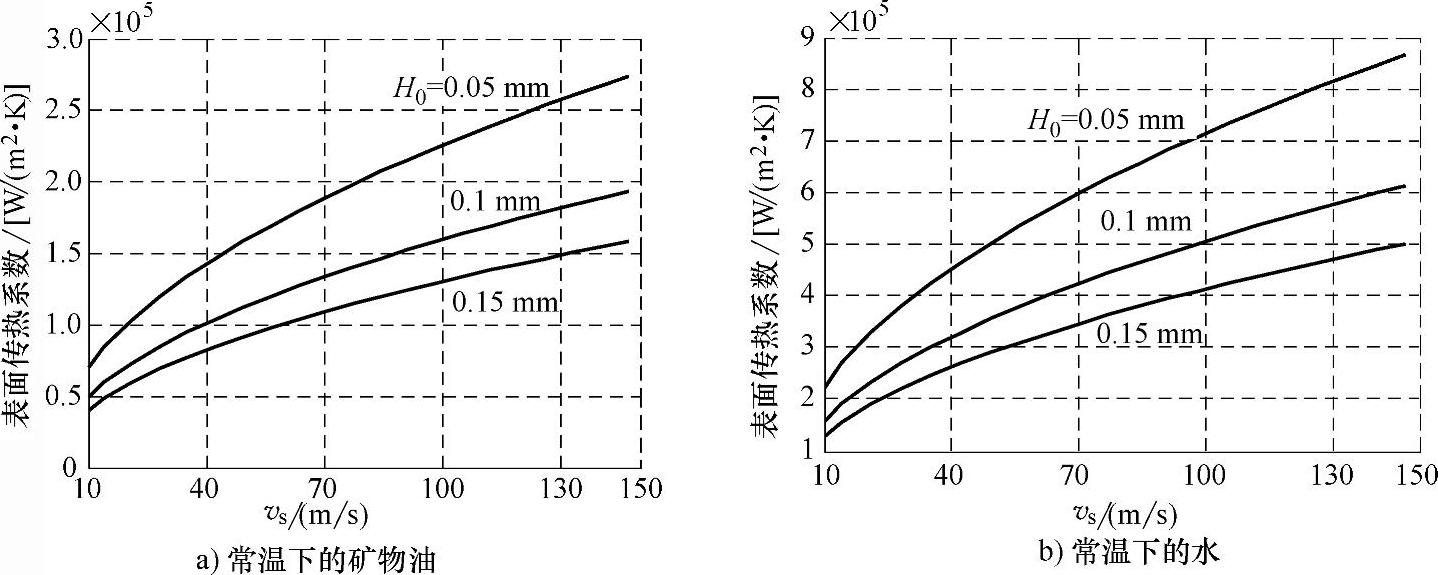
图4-10 磨削液表面传热系数h_c随砂轮速度与接触区内流体厚度的变化