砂轮与工件表面流体动压效应对流体层厚度的影响

进一步考虑在砂轮和工件表面之间薄层流体的动压效应对流体切向速度u_θ以及渗入砂轮表面的深度h的影响，对上述分析进行修正^[14]。

如果忽略砂轮表面孔隙的影响，对于层流情况，描述图4-4中∠DOE范围内砂轮与工件表面间产生的流体动压力的雷诺方程可表达为^[18]

此处将磨削液看作是在工件表面流向楔形区的具有一定厚度t的流体，∠DOE由砂轮半径R和流体厚度t决定。Guo和S.Malkin针对他们的试验条件，采用比较简单的方法，用标尺具体测量了这层流体的厚度，发现厚度t在1～3mm之间。在这一范围内，流体厚度t的取值对磨削液渗入砂轮表面的深度和流体在砂轮表面的切向速度影响很小。

图4-4中，砂轮与工件间形成的楔形区内流体厚度变化可由下式表达

式中 H₀——图4-4中交点E处的砂轮与工件之间的平均间隙值，该平均间隙取决于砂轮表面磨粒层的有效气孔率。

联立式（4-16）、式（4-17）以及式（4-19），可求得考虑磨削区内部流体动压效应的磨削液切向速度u_θ以及渗入砂轮表面深度h。

计算中采用的初始值以及边界条件如下

在流体入口处（图4-4中OD处）

θ=θ₀(www.xing528.com)

u_θ=（v₀+v_w）cosθ₀

h=0

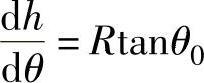
p=p₀=ρ（v₀+v_w）²/2

在交点处（图4-4中OE处）

θ=θ_c

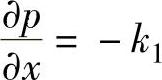
注意图4-4中x方向与图4-1不同。

假设磨削液在非常接近砂轮与工件交点处以平行于x轴方向注入磨削区（图4-4）。喷嘴出口处的流体速度v₀可以根据磨削液流量或喷嘴出口处喷射压力p₀计算。与流体动能相比，由于喷嘴高度造成的流体势能在此处可忽略。根据Engineer等人的研究结果^[9]，对于一个截面面积为113mm²的喷嘴，在一般磨削液供应条件下，从喷嘴流出的流体速度一般在0.3～0.6m/s。

式（4-16）和式（4-17）可采用四阶荣格库特方法用数值方法求解，式（4-19）是边界值问题，也可以采用有限差分方法用数值方法求解。