磨削区内流体层厚度优化方案：

在上述分析中，假设已知磨削区内薄层流体的厚度δ。在工程实际中，该厚度值与具体磨削条件和磨削参数密切相关。以往的相关研究表明，磨削区内的流体热边界厚度可以通过试验方法和理论分析进行评估^[8，9，17]，如图4-3所示。

Guo和S.Malkin对磨削区的流体流动开展了理论分析工作，对磨削区内砂轮表面的流体速度、流体渗入砂轮的深度以及磨削区内流体的有效流量进行了计算^[8]，如图4-4所示。他们的研究基于几个基本假设：（1）忽略流体重力的影响；（2）考虑二维流体流动的情况，即不考虑流体沿砂轮轴向方向流动影响。设立假设（2）是因为考虑磨削宽度一般远远大于磨削区薄层流体厚度以及砂轮表面孔隙间距。

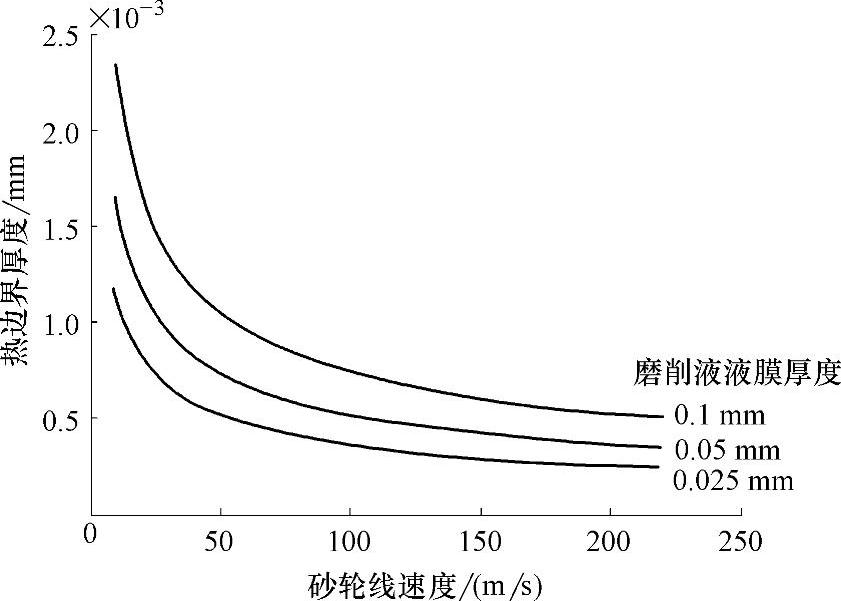
图4-3 磨削区内流体热边界厚度（水基磨削液，室温）

图4-4 磨削区流体注入情况示意图

他们通过理论分析，建立了如下关于磨削液的切向速度u_θ以及渗入砂轮表面深度h的微分方程

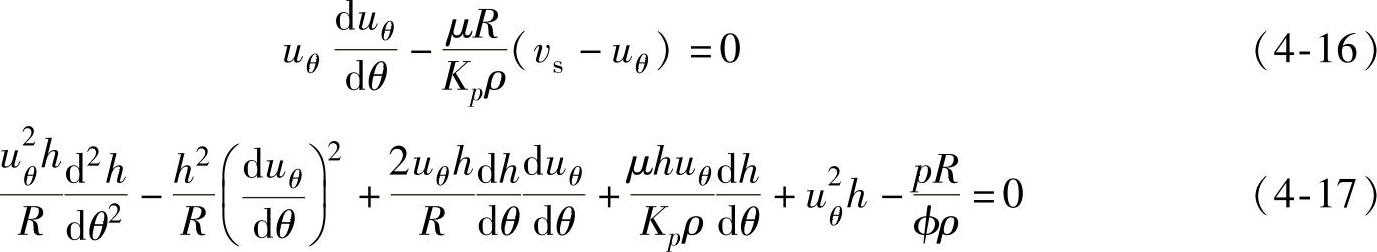
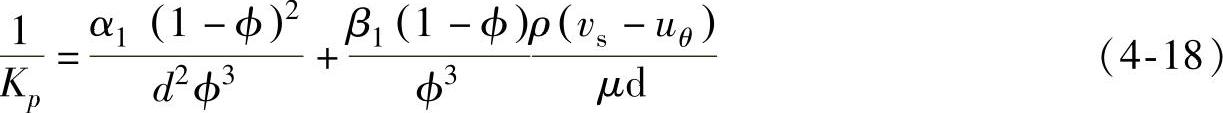
式中 θ——砂轮表面从OD处开始的角位置，其最大值为∠DOE；(www.xing528.com)

R——砂轮半径；

p——流体压力；

v_s——砂轮速度；

ϕ——砂轮表面的供流体流动的有效气孔率，对于中等组织号的普通精密磨削砂轮，其取值在为0.4，对于较大气孔率的缓进给砂轮，其取值在为0.9^[11]；

K_p——砂轮表面层的渗透性；

α₁和β₁——常数，其取值分别为150和1.75；

d——砂轮直径，对于F60～F70的砂轮，砂轮磨粒直径约为d=0.2mm。

Guo和S.Malkin采用数值方法对上述式（4-16）、式（4-17）进行了计算，计算中假设，由于喷嘴中流出的磨削液喷射压力作用，磨削液填充注入砂轮表面气孔。