磨削区内流体热边界层厚度优化方案

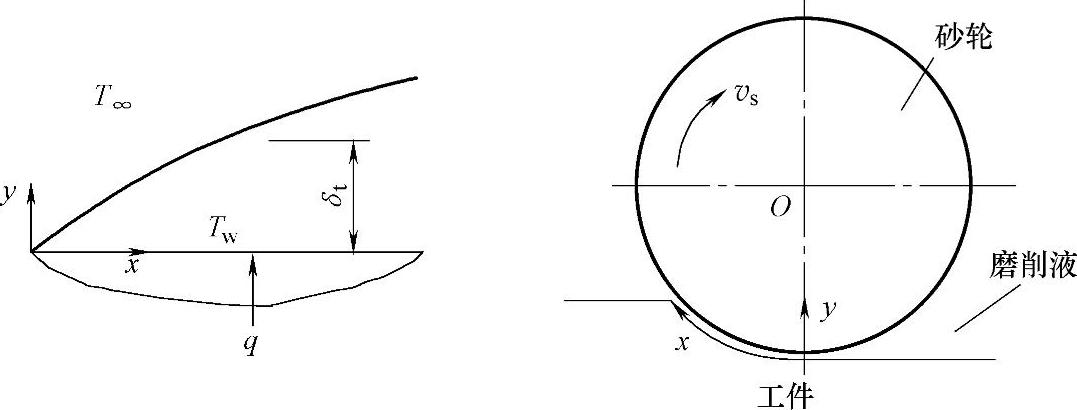
图4-1 磨削区工件表面流体热边界层

首先对磨削区内流体热边界层厚度进行理论分析^[14，15]。

图4-1所示为磨削区砂轮与工件之间形成的薄层流体通道和工件表面流体热边界层在垂直工件表面分析的温度分布。工件表面温度为T_w，简化考虑在x方向均匀分布；注入磨削区的磨削液（大部分在热边界层外，详见后续分析）平均温度为T∞；δ_t为流体热边界层在x处的厚度。假设砂轮表面处流体速度等于砂轮表面线速度v_s。后续相关分析将进一步验证这一假设。在工件表面，传入流体的热流密度可用下式表达

式中 κ——导热系数；

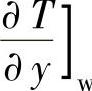——工件表面处流体的温度梯度；

h_c——流体表面传热系数。

注意此处的表面传热系数h_c对应的是工件表面平均温度。如果对应工件表面最大温度，表面传热系数为h_f，两者在数值上有所不同。

由式（4-1）可见，要求表面传热系数h_c，需要知道工件表面处流体的温度梯度值。该温度梯度可以通过分析流体在y方向的温度分布求解得出。流体温度分布必须满足的边界条件如下

T=T_w，

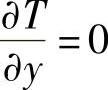，T=T∞，当 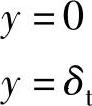（4-2）

忽略黏性耗散作用，不可压缩流体的简化能量方程为

在y=0处，无黏性加热作用

由式（4-2）、式（4-3）、式（4-4），可反推出如下方程^[16]

对于大多数磨削情况，磨削宽度一般远远大于磨削区薄层流体的厚度，在磨削区内的流体可按二维情况进行分析。在无限宽磨削区域内，流体稳态流动纳维叶-斯托克斯（Navier-Stokes）方程可表达为

式中 u——流体在x方向流动速度；

μ——流体动力黏度；

p——流体压力。

边界条件为

u=0，当y=0；

u=v_s，当y=δ。

式中 δ——磨削区薄层流体的厚度；(www.xing528.com)

v_s——砂轮表面线速度。根据上述边界条件求解式（4-6），在y方向流体速度的变化可表达为

流过砂轮与工件之间间隙的流体质量可由下式计算

式中 b——磨削宽度；

ρ——流体密度。

将式（4-7）带入上式，可导出如下表达式

沿x方向的流体压力梯度可表达为

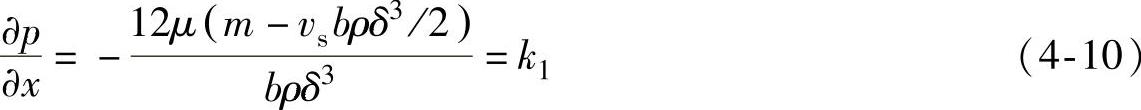
流体速度u沿y方向近似为抛物线分布，则流体质量可近似地表达为

则式（4-10）可简化为

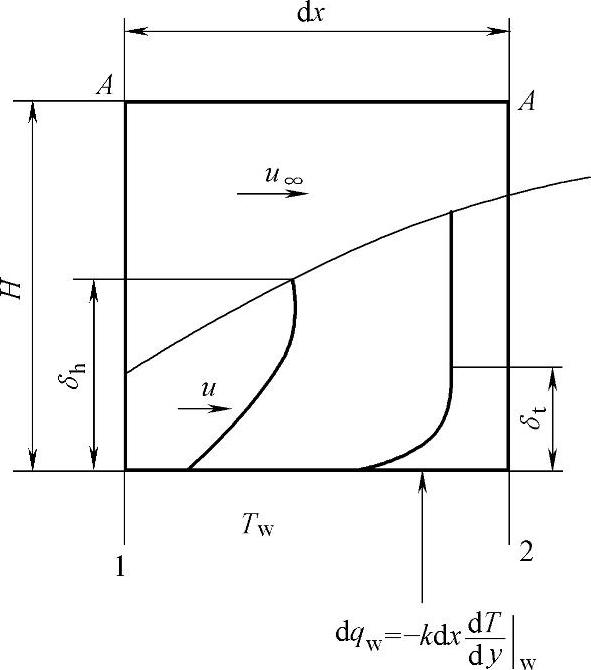
图4-2 磨削区内工件表面流体的控制体积单元

考虑磨削区内工件表面流体的控制体积单元（图4-2），其由面1，2，A-A和工件表面四个面决定。假设流体热边界层厚度δ_t小于流体动压层厚度δ_h，此假设将在后续论述中进一步证明。根据控制体积单元内的能量平衡关系，单元内流体对流黏性功dE_v与在工件表面传导的热量dE_h之和应等于对流传出的能量dE_c^[16]

dE_v+dE_h=dE_c （4-13）

据此可建立如下方程

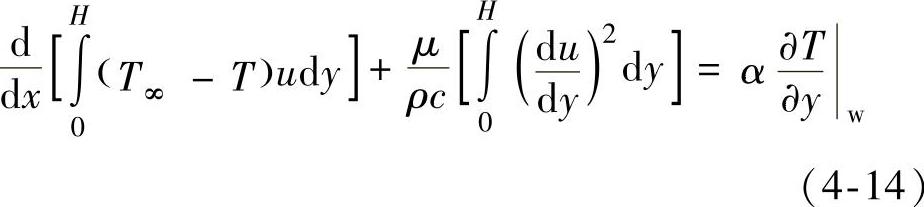
对上式积分至y=δ_t即可，在y＞δ_t以上的积分结果为零。将式（4-5）和式（4-7）带入上式，得到如下关于δ_t的关系式

A₄δ⁴_t+A₃δ³_t+A₂δ²_t+A₁δ_t+A₀=0 （4-15）

上述高次方程的各项系数为

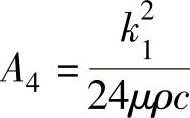
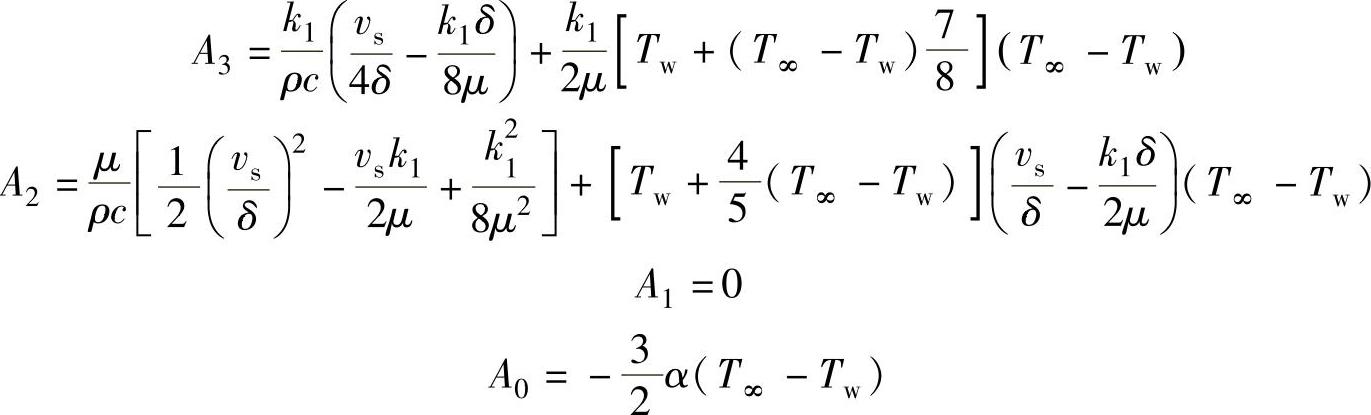
求解多项式方程（4-15），可得到4个根，其中只有一个根的数值处于热边界层厚度δ_t的合理范围，取其为有效解。采用求解获得的边界层厚度δ_t值，由式（4-1）和式（4-5）可求出磨削区内部流体的表面传热系数。