圆弧接触移动热源模型的建立与研究

在倾斜移动面热源模型中，为了简化推导过程，砂轮与工件接触面被简化为一个倾斜移动平面，与实际接触情况有所出入。金滩在英国利物浦约翰·摩尔大学工作期间和布莱恩·罗教授对上述模型做了进一步改进^[10]，将砂轮与工件接触面看作圆弧面，工件表面和内部温升通过对沿圆弧面上分布的线热源积分，模型的准确性进一步提高。

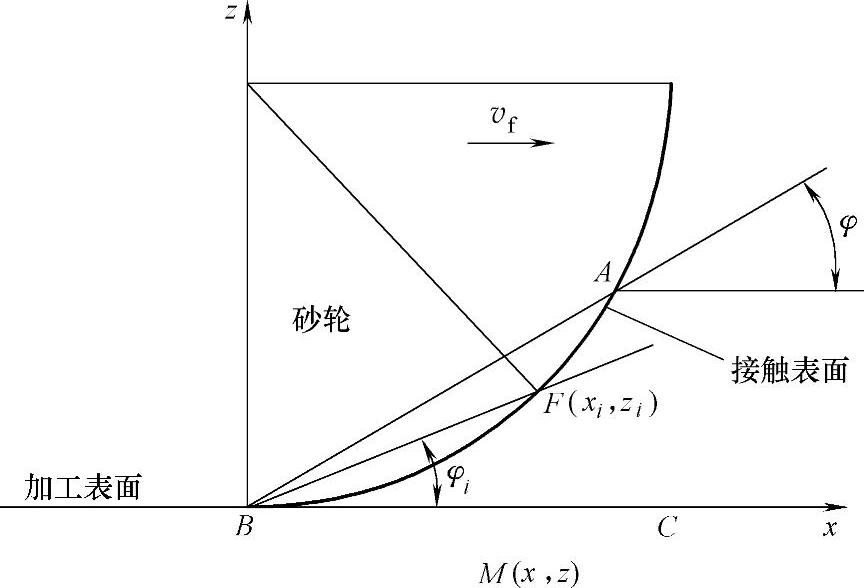
图2-16 圆弧接触移动热源模型

在倾斜移动热源模型中，接触角是一个常数，而在圆弧接触移动热源模型（图2-16）中，砂轮与工件接触面是一个圆弧面，接触长度l_c等于弧长AFB，接触角沿磨削弧方向连续变化，接触区热源由连续分布在接触弧上的众多无限长移动线热源组成。在F（x_i，z_i）点的线热源以速度v_f在平行于x轴方向移动，接触角φ_i为∠FBC，最大接触角φ等于∠AFB。接触弧长BF为l_i=d_eφ_i（d_e为砂轮等效直径）。

移动线热源dl_i，在点M（x，z）造成的温升为

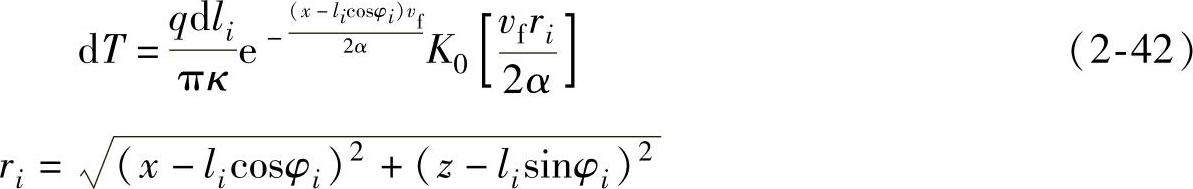
式中 K₀——零阶二类贝塞尔函数；

α——工件材料的热扩散系数；

κ——导热系数。圆弧面上总热源在点M（x，z）造成的温升为

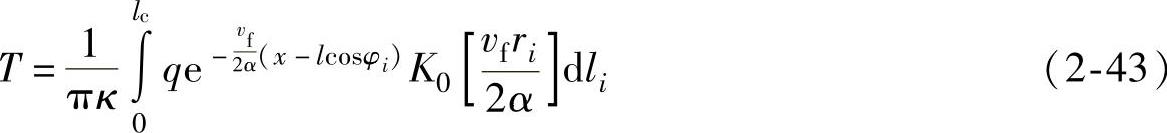
热流密度q可写成如下形式(www.xing528.com)

当n=0时，热源为均匀分布，n=1时，热源为三角形分布。q为弧长AFB面上的平均热流密度。式（2-43）可转换为无量纲形式

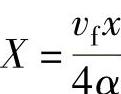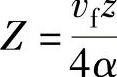，，帕克莱数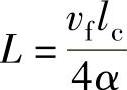，无量纲温升为由式（2-43）、式（2-44）可导出在接触面AFB、加工面BC以及工件内部任意位置的温升。

在高效深切磨削中，由于切深和工作台速度、帕克莱数和接触角φ较大，在AFB面和BC面之间存在一个楔形材料区，因而在这两个面上的温度差别较大，具体取决于帕克莱数和接触角φ的数值，是高效深切磨削热设计中需要考虑的重要因素。

图2-17为圆弧接触移动热源模型导出的接触面AFB和加工面BC上的最大无量纲温度分布。当帕克莱数L=50时，接触面和加工面上的无量纲温度均随接触角的增大而降低。加工面上的温度则低于接触面上的温度。一般来说，增大帕克莱数和接触角φ有助于降低在加工面上的温度，避免磨后热损伤。当然，实际磨削温度还与比磨削能的大小以及磨削区的热分配比率有关。

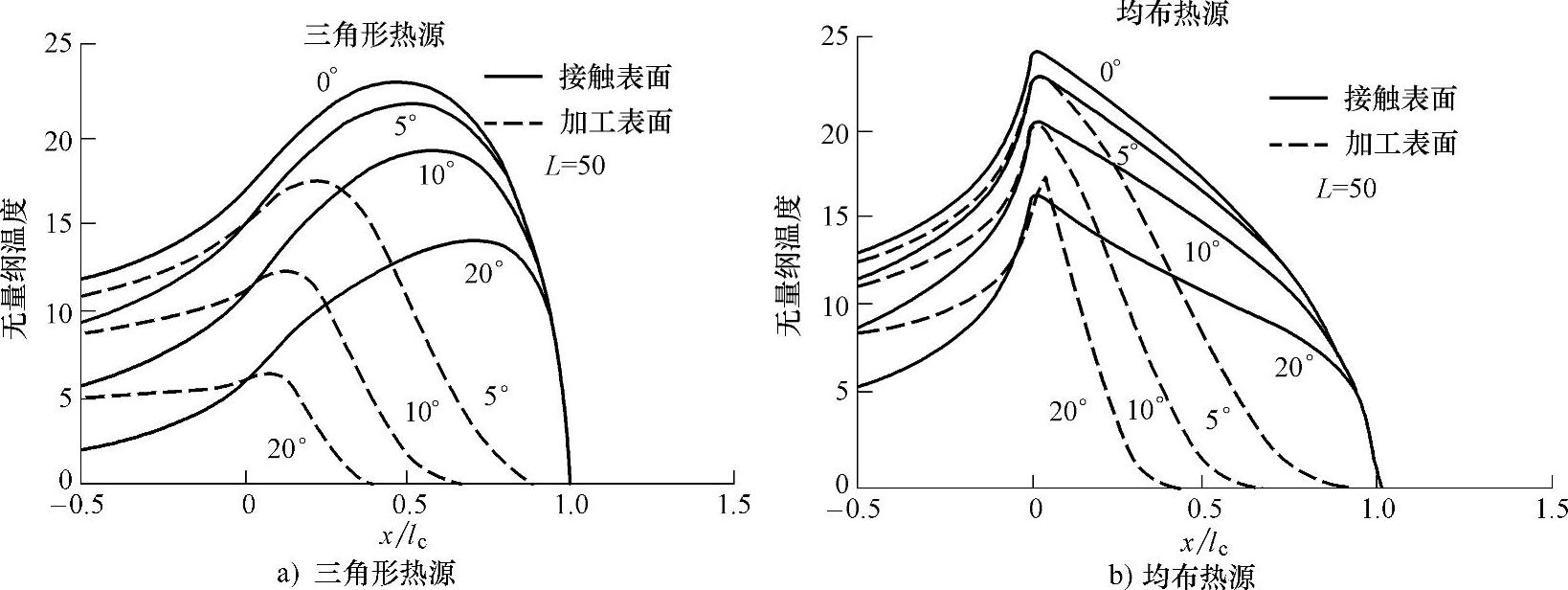
图2-17 接触面与加工面最大无量纲温度分布

圆弧接触移动热源模型导出的接触面无量纲温度较倾斜移动热源模型有所提高，而两种模型导出的加工面无量纲温度差别较大，即使在接触角较小的情况下（φ=5°），两种模型导出的加工面温度也有较大差别，如图2-18所示。圆弧接触模型比较接近实际的砂轮与工件几何接触情况，计算结果应该更加准确。

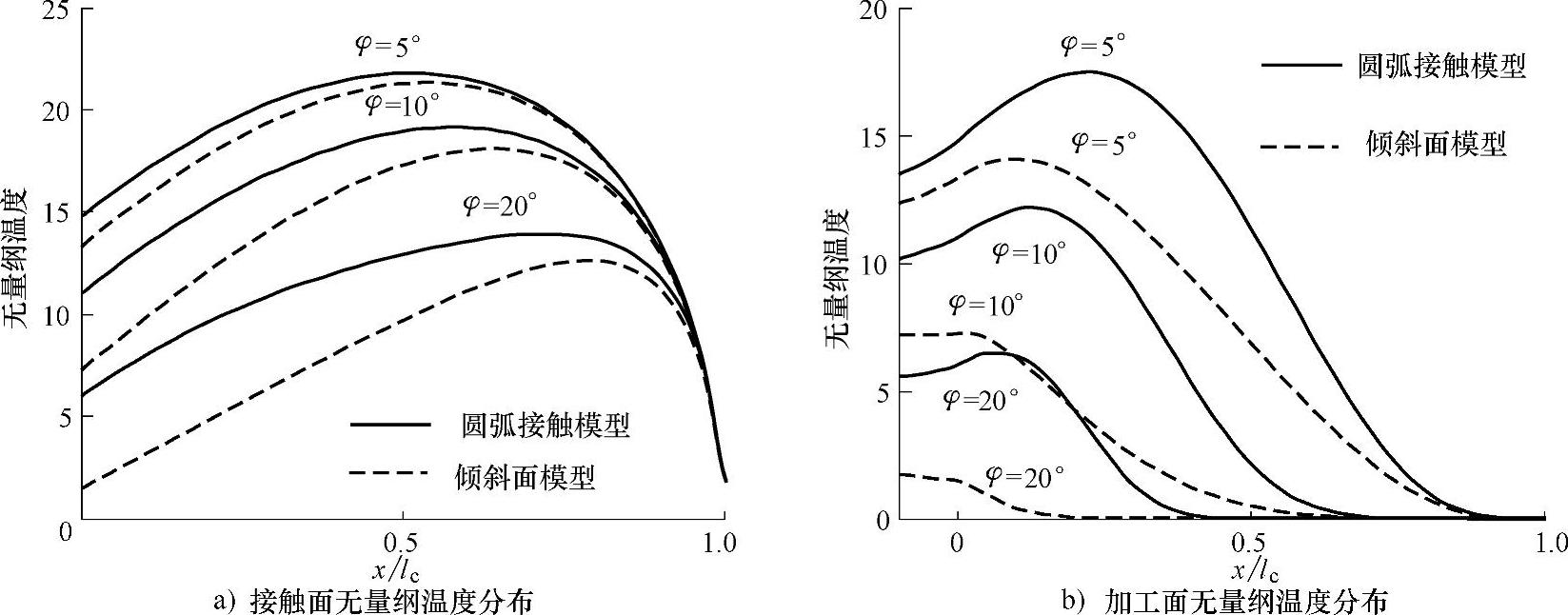
图2-18 两种模型导出的最大无量纲温度分布对比（L=50）