【摘要】：图2-11 无限大导热体中运动线热源按二维导热问题考虑，需分步求解。首先考虑在无限大导热体中，一个无限长线热源持续发热，发热功率为q，该热源同时以速度vx沿x轴平移，导热体中一点M则以速度vz平行于z轴平移，以下即求解线热源发热和运动t秒后M（x，z）处的温升。在τi时刻，运动热源所发热量qdτi对M（x，z）处造成的温升按无限大导热体中瞬时线热源温度场公式计算式中各变量关系见图2-11，τ=t-τi。
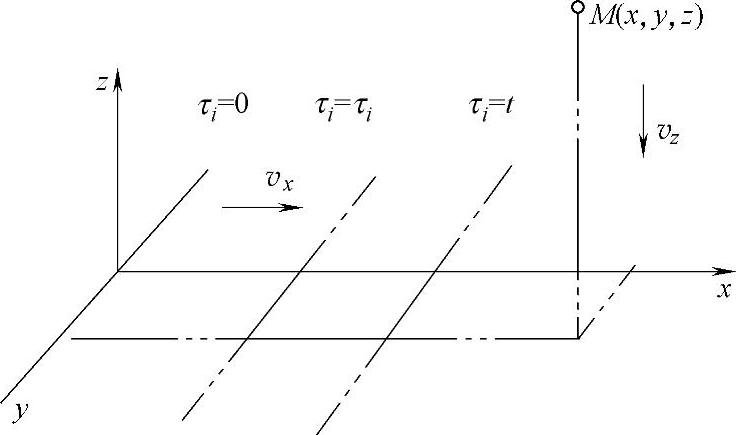
图2-11 无限大导热体中运动线热源
按二维导热问题考虑，需分步求解。首先考虑在无限大导热体中，一个无限长线热源持续发热，发热功率为q，该热源同时以速度vx沿x轴平移，导热体中一点M（x，y，z）则以速度vz平行于z轴平移（见图2-11），以下即求解线热源发热和运动t秒后M（x，z）处的温升。
在τi时刻，运动热源所发热量qdτi对M（x，z）处造成的温升按无限大导热体中瞬时线热源温度场公式计算
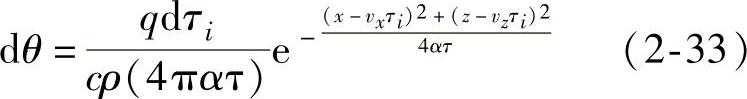
式中各变量关系见图2-11，τ=t-τi。取动坐标x′=x-vxt，z′=z-vzt。从τi=0到τi=t，运动线热源的总影响造成M处的温升
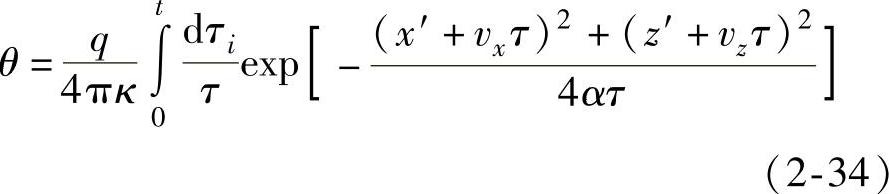
式中 κ——热传导系数。
解得
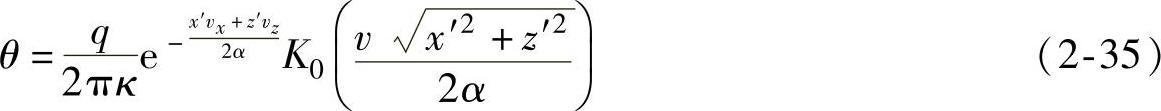
式中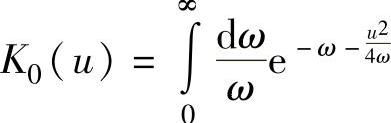 
。
当积分上限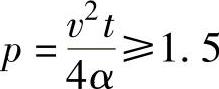
时，即可认为
。
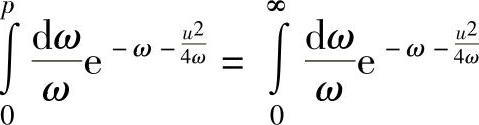将斜面AB上的面热源q看成线热源（y方向）的综合，并建立图2-11动坐标系x′z′与热源一起以速度v运动。各个线热源沿v方向运动，即vx=vcosφ，vz=vsinφ。半无限大导热体表面AB附近一点M（x′，z′）受dxi′线热源影响的温升由式（2-35）及镜像热源原理计算
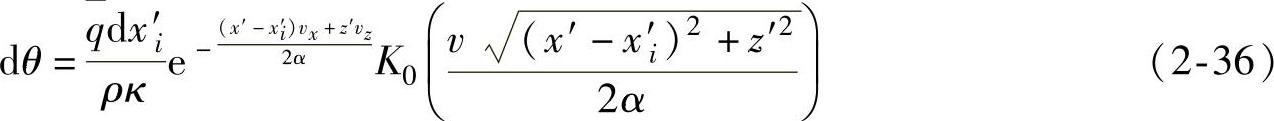
则M（x′，z′）受整个面热源影响的温升为(www.xing528.com)
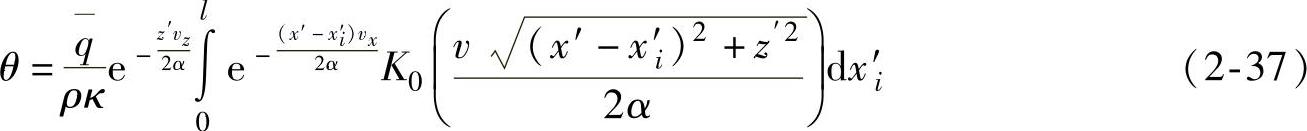
在热源作用表面（z′=0）
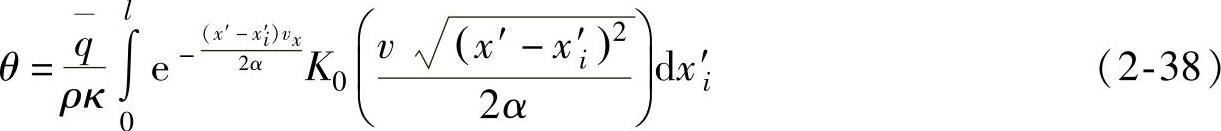
解得
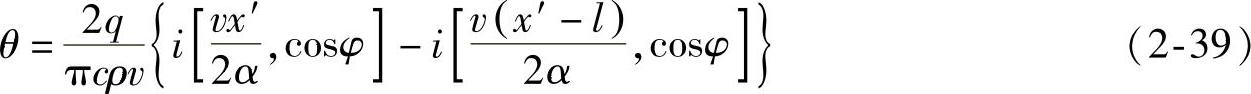
式中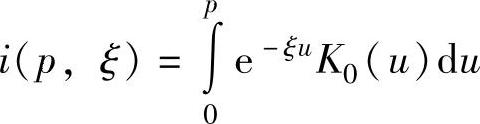 
。
表面无量纲温升为
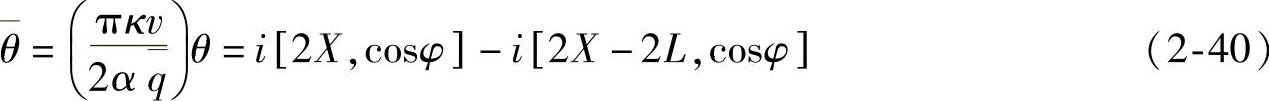
当φ=0，cosφ=1时
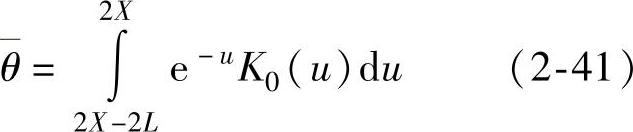
与Jaeger的解完全相同，即Jaeger的解是倾斜运动传热问题的一个特例。由此也从一个角度验证了上述有关假设和推导的正确性。
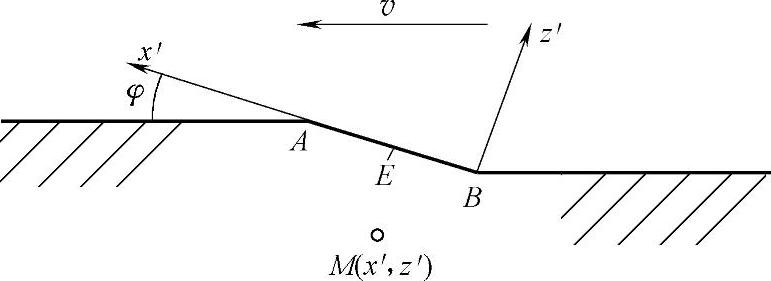
图2-12 均布热源二维传热
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
