1.均布热源模型
在倾斜热作用表面上建立图2-9所示的坐标系。A′B′斜面上均布热源的热流强度为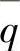 。造成斜面AB温升的热量来自邻近运动斜面A′B′上的均布热源,该热源随A′B′以速度v向AB移动,并沿z轴一维传热,随着A′B′与AB趋近,z值减小,热量传递逐渐由B到A,AB斜面温度不断提高,直至A′B′与AB重合。
。造成斜面AB温升的热量来自邻近运动斜面A′B′上的均布热源,该热源随A′B′以速度v向AB移动,并沿z轴一维传热,随着A′B′与AB趋近,z值减小,热量传递逐渐由B到A,AB斜面温度不断提高,直至A′B′与AB重合。
取AB=A′B′=l,l为磨削弧长,则A′B′上热源对AB的作用时间为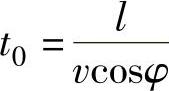 ,在τi时刻的一个瞬间dτi,A′B′热源瞬间发热量为
,在τi时刻的一个瞬间dτi,A′B′热源瞬间发热量为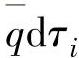 ,从该瞬间到t0的时间间隔为τ(τ=t0-τi)。将A′B′看成半无限大导热体表面,受瞬时发热影响,AB上某点
,从该瞬间到t0的时间间隔为τ(τ=t0-τi)。将A′B′看成半无限大导热体表面,受瞬时发热影响,AB上某点
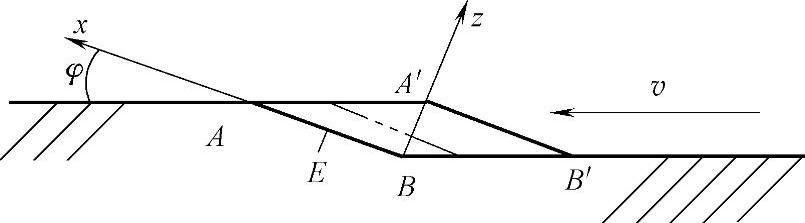
图2-9 均布热源一维传热
E(x,0)的温升可按无限大导热体中瞬时无限大面热源温度场公式和镜像热源原理[12,13]计算

式中 z=z0-vzτi;
z0=A′B=vzt0;
vz=vsinφ;
c、ρ、α——工件材料的比热、密度和导热系数;
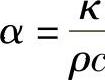 ;
;
κ——导热系数。E点开始受到A′B′热源作用的时间为: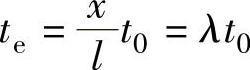 ,0≤λ≤1。则从τi=te到τi=t0,E点温升为
,0≤λ≤1。则从τi=te到τi=t0,E点温升为
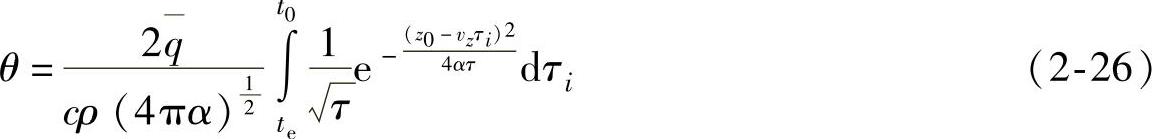
解得 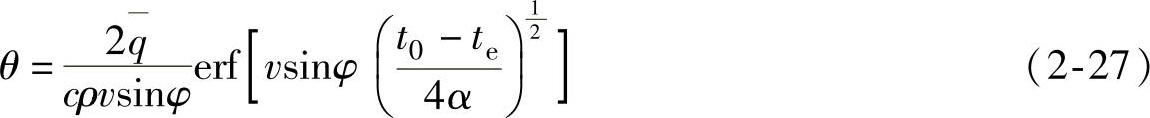
其中误差函数 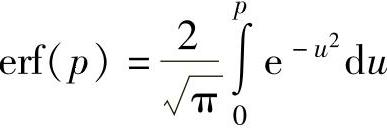
式中 p——积分上限;(https://www.xing528.com)
u——积分变量。
将式(2-27)写成无量纲形式
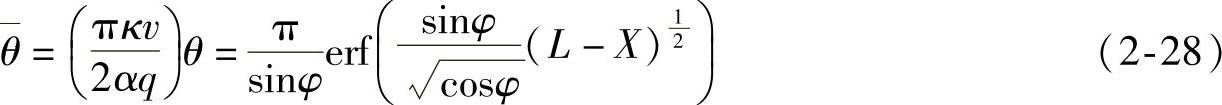
式中 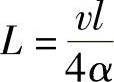 ;
; 。
。
2.三角形分布热源模型
在磨削弧上,磨粒的磨削厚度是不均匀的,在接触弧前方最大,至尾部逐渐减小。取A′B′上热流为三角形分布(图2-10),则在τi时刻(te≤τi≤t0)的一个瞬间dτi,A′B′热源在E点上方瞬间发热量为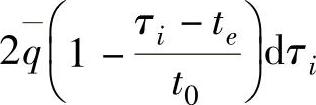 ,从该瞬间到t0的时间间隔为τ(τ=t0-τi)。受瞬时发热影响,半无限大物体表面A′B′附近一点E(x,0)的温升按无限大导热体中瞬时无限大面热源温度场公式和镜像原理[12,13]计算
,从该瞬间到t0的时间间隔为τ(τ=t0-τi)。受瞬时发热影响,半无限大物体表面A′B′附近一点E(x,0)的温升按无限大导热体中瞬时无限大面热源温度场公式和镜像原理[12,13]计算
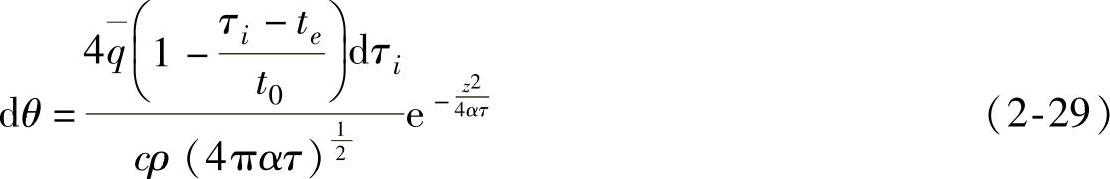
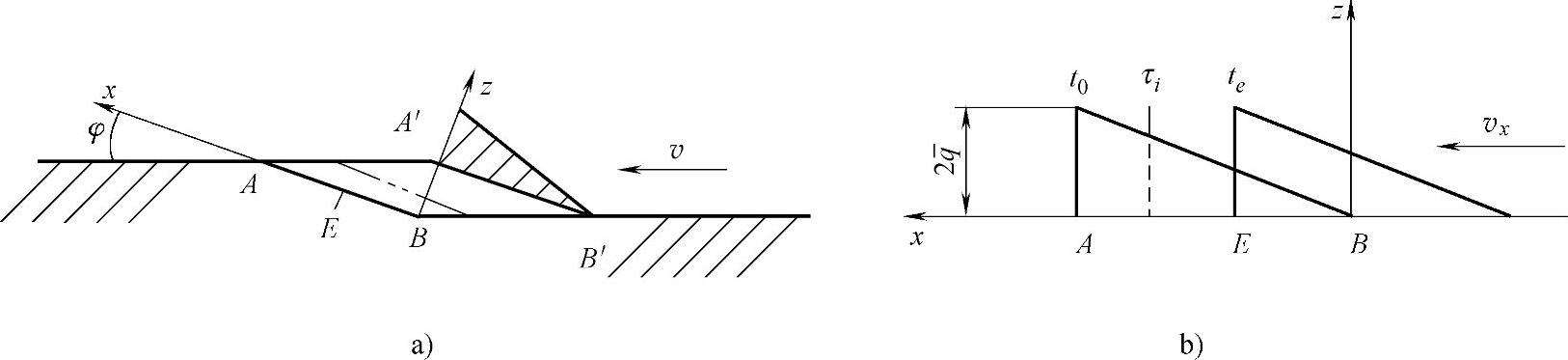
图2-10 三角形分布热源模型
则从τi=te~t0,E点温升为
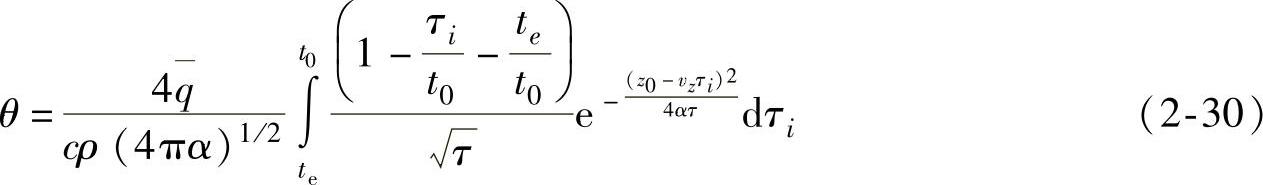
经分步积分得
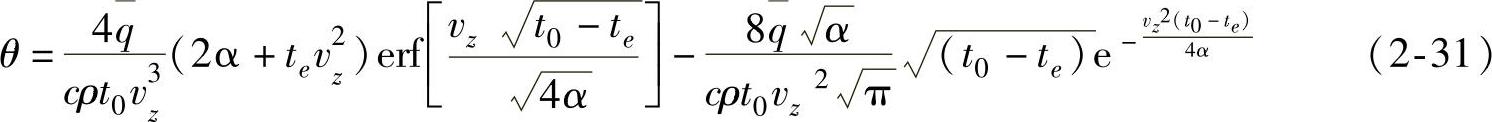
写成无量纲形式
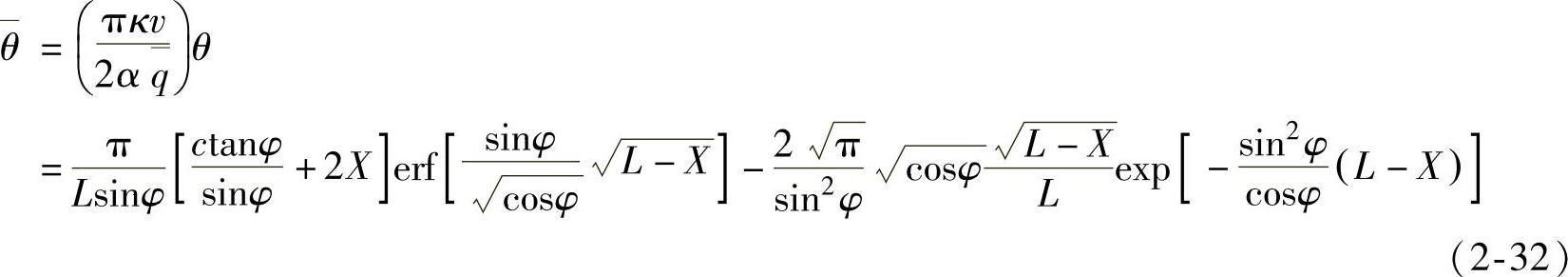
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




