应用案例：实际状态下热误差建模参数优化

热误差特性随着参数的变化而变化，但在参数变化一定的范围内。如果热误差的变动在可接受的范围之内，则在工程上可认为能够忽略相关参数的影响。但对于热误差模型来说，在一定的参数变化范围内，必然希望建模数据所包含的信息最能反映当前范围内的热误差特性。

实验中发现，如果在热误差测量阶段，改变机床的一些影响因素，也会导致测量数据中包含的热误差特性信息有所差异，进而使建立的模型预测精度出现差异。因此，会不会存在某种比较好的参数组合，能够从测量阶段进一步优化热误差模型，值得探究。

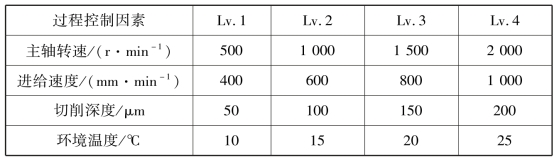
作为应用案例，借助于田口正交实验法，在实际切削条件下，针对Leaderway V-450 机床的主轴Z 向热变形，探究主轴转速、进给速度、切削深度和环境温度4 种因素对热误差建模效果的影响，最终目的是找出抗干扰能力强、调整性好、性能稳定的最佳参数水平组合，提高模型预测精度及稳健性。控制因素及其水平见表7-11。

表7-11　控制因素及水平表

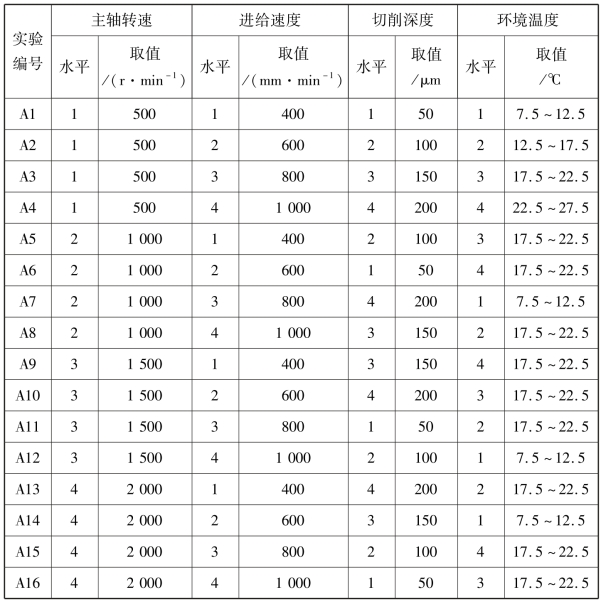
对于该4 种因素水平，采用正交表L16（44）安排实验计划，具体实切实验设计参数见表7-12。

表7-12　实切实验参数设计表

根据表7-12 所示的参数组合，当环境温度变化至对应水平时，进行热误差实验，其中A1、A9 和A16 批次实验数据分别如图7-27、图7-28 和图7-29 所示。

根据A1 ～A16 批次数据，利用稳健性数控机床温度敏感点选择方法对温度敏感点进行选择，并利用稳健性算法建立温度敏感点和热误差之间的模型，温度敏感点选择结果见表7-13，模型建立结果见表7-14。

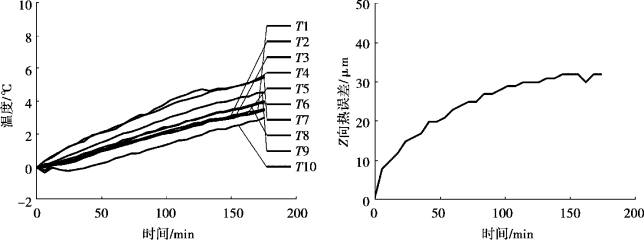
图7-27　A1（实切）批次温度（左）和热误差（右）测量数据

图7-28　A9（实切）批次温度（左）和热误差（右）测量数据

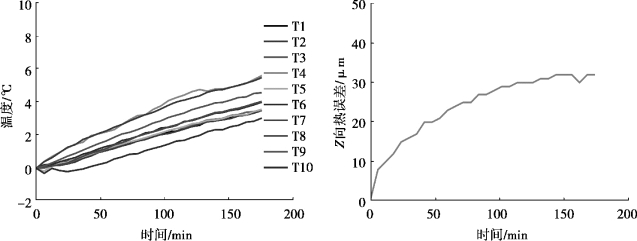
图7-29　A16（实切）批次温度（左）和热误差（右）测量数据

表7-13　A1 ～A16 温度敏感点选择结果

表7-14　A1 ～A16 热误差模型

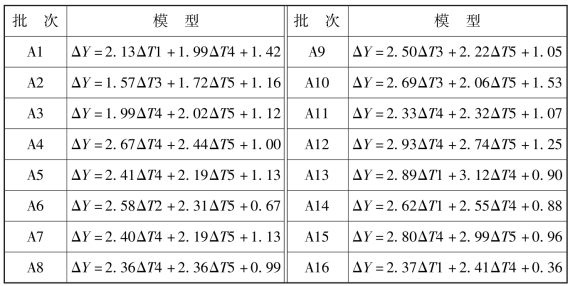
其中，ΔY 为热误差量，ΔT1 ～ ΔT5 为传感器测得的温度敏感点温度变化量。(www.xing528.com)

结合田口实验法给出的分析方法，通过模型的预测精度来探究主轴转速、进给速度、切削深度和环境温度4 种因素对热误差模型的影响，具体如下。

信噪比（SNR）作为评价通信设备、线路、信号质量等优劣的指标，采用的是（Signal）的功率和噪声（Noise）的功率之比。田口博士将信噪比的概念引入正交实验中，以信噪比作为衡量产品质量稳定性的指标，越大表示质量越好。本节以信噪比作为衡量模型预测效果的指标，对正交实验结果进行统计分析。信噪比计算公式如下。

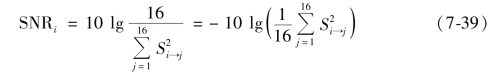
式中，SNRi 表示Ai 批次数据建立的模型的信噪比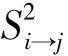，为Ai 批次数据建立的模型对Aj 批次数据预测得到的残差平方和，计算方法如下。

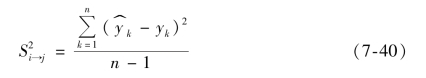
其中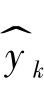 为Ai 批次数据建立的模型对Aj 批次数据预测得到的第k 个预测值，yk 为Aj 批次数据对应的第k 个测量值。最终的计算结果见表7-15。

表7-15　A1 ～A16 批次实切实验模型信噪比

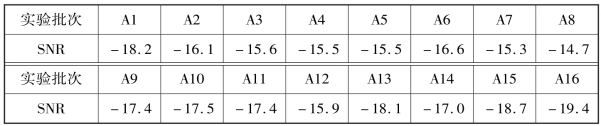
根据表7-15 的计算结果，可通过主因素分析来获取各因素实切状态对热误差模型的影响权重，并提取最佳参数组合。

首先计算各因素在对应水平下的信噪比均值，比如要计算主轴转速在水平1（500 r/min）下的平均值，可将A1 ～A4 批次实验数据模型得到的信噪比进行平均，即

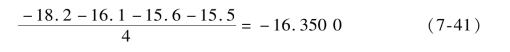
最终的计算结果见表7-16。

表7-16　各因素水平的平均信噪比

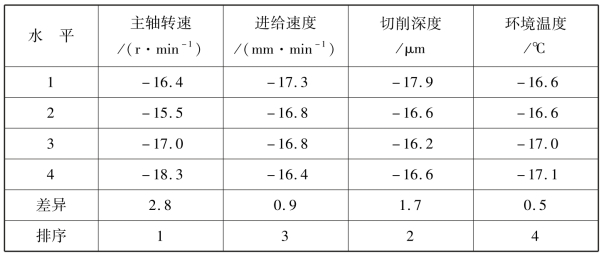
如表7-16 所示，各因素水平下的平均信噪比反映了此因素在将其他因素视为随机误差的条件下，单独作用的结果。如果对于某个因素，在不同水平下的平均信噪比差异越大说明此因素对热误差模型的影响越大。通过表7-16可以看出主轴转速的差异达2.8，影响最大。最小的是环境温度，仅为0.5。

将每个因素下平均信噪比最高的因素选入最佳参数组合，结果为主轴转速1 000 r/min、进给速度1 000 mm/min、切削深度150 μm 以及12.5 ～17.5 ℃的环境温度。

为了验证得到的最佳参数组合，另进行了一组16 批次重复验证热误差测量实验，记为B1 ～B16批次，除了B8 批次是按照最佳参数组合设置，其余批次均仿照表7-8 中A1 ～A16 批次的实验参数进行设置。

参考式（7-37）和式（7-38），分别计算B1 ～B16 批次实验数据建立模型的信噪比，见表7-17。

表7-17　B1 ～B16 批次实切实验模型信噪比

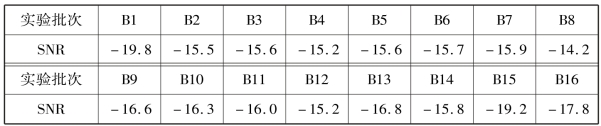
从表7-17 可以看出，按照最佳参数组合设置的B8 批次实验，得到的信噪比最高，说明利用田口正交实验的确能够对热误差模型的预测效果起到提升作用。