建模和精度验证：全面介绍

1）实验装置

以典型的C 型数控机床LeaderwayV-450 立式加工中心为研究对象，具体热误差测点分布位置如图7-14 所示。温度采集系统选用温度传感器DS18B20 用于测量温度数据。温度传感器的安放位置如图7-19 和表7-4 所示；坐标采集系统是由在线检测系统（包含测头和红外接收器）、机床外扩I/O单元、坐标采集卡和计算机组成。其原理是获得在线检测系统测量测头当前所在位置坐标，通过机床外扩I/O 单元将此坐标值输出到坐标采集卡中，并利用坐标采集卡将坐标值输入计算机，最终完成坐标采集。同一温度时刻，工作台不同测点坐标值拟合出的曲面为该温度平面度评定标准，而不同温度时刻，各测点的坐标值偏差为该点Z 轴热误差数据。

实验数据测量时，温度数据和热误差数据为同步测量。温度采集系统和坐标集系统实物图如图7-20 所示。

图7-19　温度传感器及测点分布示意图

注：T1 ～T9 为温度传感器编号（T10 未在图中画出）；1 ～15 为工作台上15 个测点的编号。

表7-4　传感器安放位置及作用

图7-20　温度采集系统和坐标采集系统实物图

2）机床综合误差补偿方案确定

（1）工作台Z 轴轴向变形特征分析

根据第一批实验数据绘制10 个温度传感器采集的温度值变动趋势图，如图7-21 所示。选取温度提升过程中主轴区域温度值变化值较大的3 个时刻，即第0 min、第30 min 和第180 min 时刻的工作台上15 个点位置对应的坐标值，利用3 次样条函数曲面插值法，画出该时刻工作台面形态图，如图7-22所示。

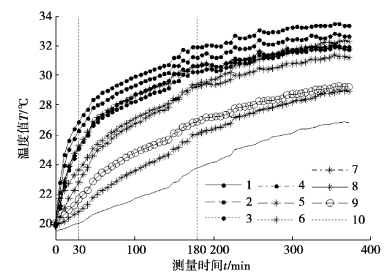
图7-21　温升趋势图

注：图中的1—10 为10 个温度传感器的编号；竖虚线为所截取的测量时刻。

分析图7-22 可知，工作台面存在初始的平面度误差，即工作台各点初始坐标存在差异。随着温度的升高，工作台沿主轴Z 方向呈整体上升趋势，但随着温度的变化，形状并没有较大改变，即各点之间的坐标值差异依然基本保持不变。从所测数据中提取各被测点Z 轴坐标，并计算相应的热变形量，得各点处Z 轴热变形量的趋势图，如图7-23 所示。

分析图7-23 可知，在实验中工作台各点热误差均沿机床Z 轴轴向发生热变形，规律性明显。同一测量时刻工作台各点Z 轴的热变形量相差在5 μm之内，得出工作台整体平面度误差，即平面内各点之间的相对误差变化不大，这与图7-22 得出的结论一致。

（2）工作台Z 轴轴向综合误差补偿方案确定

工作台各点热误差均沿Z 轴轴向发生热变形，并且工作台平面度误差保持不变，故针对工作台热误差和平面度误差采用分开建模的补偿方法。先对工作台初始面的形状进行拟合建模，建立起工作台的初始平面度误差模型f（X，Y），该模型根据X、Y 任意坐标求出其所在位置平面度误差。再根据工作台各测点Z 轴轴向热误差变化规律，拟合出15 个测点的热误差模型Zj（j=1，2，…，15），并选择一处最优的热误差模型Zj。然后将所选热误差模型与工作台初始平面度误差模型叠加，构建一个针对全工作台Z 轴轴向综合误差补偿的模型。

图7-22　工作台面第0 min、30 min、180 min 形态图

图7-23　第一批实验工作台15 点Z 轴的热变形趋势

因此，建立全工作台Z 轴轴向综合误差补偿模型如下：

式中z 为全工作台Z 轴轴向综合误差补偿值。

3）综合误差模型建模过程

（1）热误差模型的建立

多元线性回归建模是机床热误差模型的常用建模方法，是以温度值增量为自变量，热变形量为因变量进行建模。在建模过程中，常使用模糊聚类和灰色关联度相结合的方法，筛选出温度敏感点作为变量，在保证所建模型精度的同时，来降低过多温度变量带来共线性误差的影响。按照温度敏感点筛选方法，选定温度传感器T1 和T8 作为温度敏感点来进行建模。假设实验时工作台每点位置测量次数为n 次，则其通用表达式为：

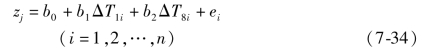
式（7-34）中，（ΔT1i，ΔT8i）为温度敏感点处的第i 次测量时刻温度值增量，（b0，b1，b2）为相应温度变量的回归系数估计值，zj 为j 点热变形测量值，ei 是与实际测量值zj 存在的偏差，也称残差。

现根据式（7-34），针对第一批实验全工作台15 点测量数据进行多元线性回归建模，所建模型系数和标准差见表7-5。

表7-5　工作台15 处回归模型参数

表7-5 中，b0 为常数项；b1 为温度敏感点T1 的回归系数估计值；b2 为温度敏感点T8 的回归系数估计值；1，2，…，15 为工作台15 个位置点；si 分别为工作台15 个位置点所建热误差模型的拟合标准差，i=1，2，…，n。

（2）热误差模型的选取

根据Z 轴轴向误差综合补偿建模的要求，本节需要在15 处热误差模型中选取一处模型参与综合建模。故通过各个点的模型对全批次数据的预测精度分析法来判别最优热变形建模位置点。将15 处模型分别对第二批次和第三批次实验数据进行预测，得出预测标准差见表7-6。

表7-6　第一、二、三批次15 处模型的预测标准差　单位：μm

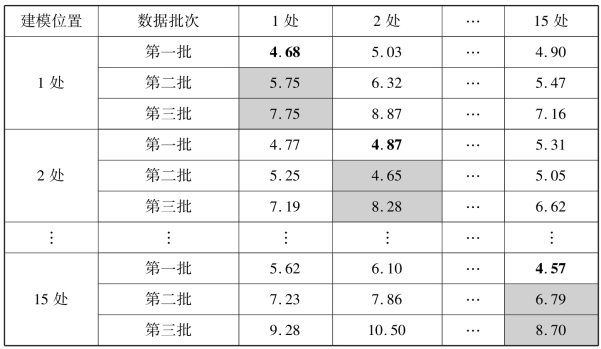
注：表中加粗部分为工作台各位置点处对自身的多元线性回归拟合的标准差；灰色部分为对同一位置其他批次的预测标准差。(www.xing528.com)

通过对表7-6 中的标准差进行进一步分析，将每一个模型的45 个预测精度参数给予平均化和离散化，分别得到每一个模型的预测精度平均值参数Mn和预测精度离散标准差参数Sd。Mn 越小，表示模型平均预测精度越高；Sd 越小，表明模型的预测稳健性越强。第一批次15 处模型预测精度参数Mn 和Sd结果见表7-7。

表7-7　第一批次15 处模型预测精度　单位：μm

将表7-7 中数据以折线图的方式表示，如图7-24 所示。

由图7-24 可得，工作台上2、5、8、11 和14 位置点所建模型对其他各批次预测精度相对于相邻点位置较小，并且第8 位置点最小。结合图7-19 中工作台各测点的位置分布，得知工作台上测点2、5、8、11 和14 点位于Y 轴的中心线上。并且第8 位置点同时处于工作台X 轴方向中心线上，即为工作台中心位置点处。所以得出位于工作台Y 轴中心线上的位置点所测数据比较稳定，所建热误差模型对其他批次数据预测效果更好，同时工作台中心位置点所建热误差模型对其他批次数据预测效果最好。

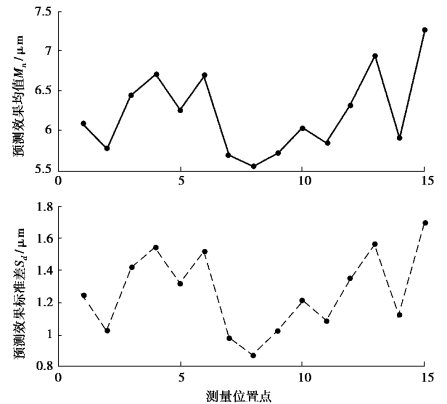
图7-24　第一批次15 处模型预测精度趋势图

经分析得出原因：本节实验所选取的机床为典型的C 型数控机床，机床X轴方向的整体结构基本呈对称布局，其热变形随温升变化较小；相对来说，Y轴的非对称结构导致其热变形较大。Y 轴中心线上的位置点抵消掉了部分Y轴方向的热变形影响，所以其预测效果好于没有抵消Y 轴方向的热变形影响位置点。第8 位置点为工作台中心点，其所处空间位置为机床的X、Y 轴中心线对称处，同时抵消了X、Y 轴热变形导致工作台倾斜等影响，热变形比较稳定，所以其所建模型预测其他位置热变形精度最小。故本节最终选取第8 位置点所建热误差模型参与综合误差补偿建模。

选取表7-5 中所求的工作台第8 位置点处的热误差模型如下所示：

式中，ΔT1i为T1 温度敏感点第i 测量时刻温度相对于第0 测量温度时刻的增量值；ΔT8i为T8 温度敏感点第i 测量时刻温度相对于第0 测量温度时刻的增量值；z8 为工作台中心位置点第8 点热变形补偿值；s8 为第8 点的拟合标准差。

（3）全工作台平面度误差模型的建立

工作台平面度误差建模，采用最小二乘曲面拟合的算法，拟合出工作台初始曲面方程。为使补偿模型运算简单且能反映工作台平面的特性，选择用二元三次多项式的模型进行建模：

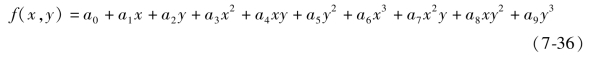
式（7-36）中，（a0，a1，…，a15）为相应变量的系数估计值；x 为机床加工工件时X 轴坐标值；y 为机床加工工件时Y 轴坐标值； f（x，y）为主轴在工作台上坐标为（x，y）时机床Z 轴的热误差补偿值。

对平面进行最小二乘曲面拟合时，由测量的工作台初始平面坐标值确定曲面常数。由实验所测工作台15 点位置坐标（0，0，4）、（0，150，0）、（0，300，6）、（100，300，8）、（100，150，6）、（100，0，11）、（200，0，11）、（200，150，6）、（200，300，8）、（300，300，8）、（300，150，8）、（300，0，8）、（400，0，3）、（400，150，3）、（400，300，8）。依据公式（7-36）拟合的热误差曲面模型如下：

（4）建立综合误差补偿模型

根据公式（7-33），由以上计算的工作台中心位置点处（第8 点）所建热误差模型公式（7-35）和工作台平面度误差模型公式（7-37）合并成如下模型：

即全工作台Z 轴轴向综合误差补偿模型如下：

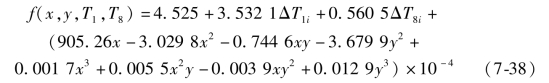
4）模型补偿精度分析

（1）全工作台综合误差模型预测精度分析

上述机床全工作台综合误差模型对第二、三批实验全工作台各温度时刻进行预测分析，得出预测的最大残差和残余标准差见表7-8。

分析表7-8 可得，预测第二批实验数据时，综合模型对工作台各个温度时刻预测残余标准差分布范围为1.39 ～10.33 μm，最大残差分布范围为2.37 ～12.06 μm；预测第三批实验数据时，预测残余标准差分布范围为1.36 ～9.81 μm，最大残差分布范围为2.65 ～12.45 μm。

表7-8　综合模型对全工作台每个测量时刻预测的最大残差和残余标准差单位：μm

（2）传统工作台固定单位置点模型预测精度分析

按照传统工作台固定单点热误差建模补偿的方法，根据3.2 节，以工作台最优建模位置点第8 点为例，同样选定温度传感器T1 和T8 作为温度敏感点，所建立热误差补偿模型如式（7-35）所示。对第二、三批实验全工作台各温度时刻进行预测分析，得出预测最大残差和残余标准差见表7-9。

表7-9　单点热误差模型对全工作台每个测量时刻预测的最大残差和残余标准差单位：μm

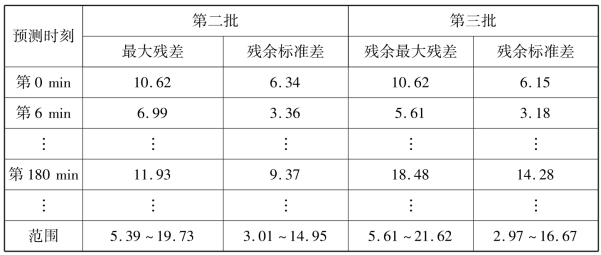
分析表7-9 可得：预测第二批实验数据时，传统单点热误差模型对工作台各个温度时刻预测残余标准差分布范围为3.01～14.95 μm，最大残差分布范围为5.39～19.73 μm；预测第三批实验数据时，预测残余标准差分布范围为2.97 ～16.67 μm，最大残差分布范围为5.61 ～21.62 μm。

（3）预测精度对比分析

将表7-8、表7-9 各批次实验按照不同建模方法预测结果绘制曲线图，如图7-25、图7-26 所示。

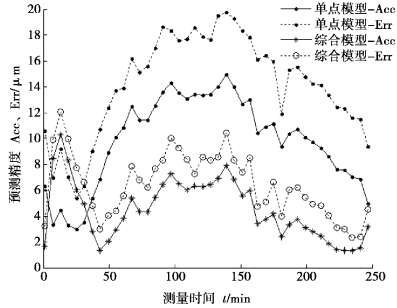
图7-25　对第二批次实验数据的预测效果图

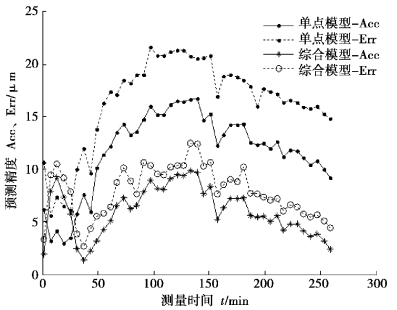
图7-26　对第三批次实验数据的预测效果图

分析图7-25、图7-26，综合模型对工作台各个温度时刻的预测残余标准差和最大残差均低于传统单点热误差模型。对第二批次实验数据预测时，综合建模预测比传统单点建模预测标准差最大提高了7.14 μm，残差的差值最大减小11.31 μm。同时对第三批实验数据预测时，预测标准差最大提高了7.09 μm，残差的差值最大减小11.30 μm。

故本著作提出的Z 轴轴向综合误差模型对整个工作台误差预测效果优于根据工作台单点测量数据建立的热误差模型，预测标准差提升了约7 μm，补偿效果提升了50%；单次最大补偿精度提升约11 μm，补偿效果提升了60%。