全区域热误差建模工作台优化

要对全工作台范围热误差进行补偿，仅依靠单点建模算法是不够的，全工作台范围热误差补偿模型需要能够反映整个工作台位置变化的影响，即模型自变量除了温度之外，还应该有能够反映工作台位置的变量。因此，本节提出建立可在工作台全区域范围内，根据工作台位置变动进行自适应调整预测的热误差模型。

考虑到热误差是温度场变化引起的，机床中热源变化较为平缓，不存在热源突变的情况，因此，温度场在空间中分布的阶次不会很高，整个工作台虽然不同位置热误差有差异，但通过图7-15 和图7-16 的测量结果也可以看出，整体变化仍然较为平缓。因此，本节采用曲面建模技术，通过多个离散点的热误差特性，选择合适的曲面模型，将其延续至整个工作台，从而实现对工作台任意位置热误差进行预测。曲面建模具体过程如下。

对工作台上所有测点测得的热误差数据进行分析，利用强稳健性建模算法，分别选出各点对应的温度敏感点，并建立热误差补偿模型。比如，在整个工作台选取了P 个热误差测点，建立得到的P 个热误差补偿模型如下：

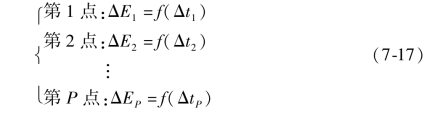
其中ΔE1，ΔE2，…，ΔEP 分别表示各点热误差，Δt1，Δt2，…，ΔtP 分别表示各点热误差补偿模型对应的温度敏感点。

如果在某一时刻，分别对上述各点的热误差进行预测，则可以得到一个覆盖工作台全区域范围的热误差离散点图，之后分别根据各点热误差值，以及位于工作台上的坐标位置，通过拟合或者插值算法建立整个工作台热误差随坐标位置变化的曲面函数。如图7-17 所示。

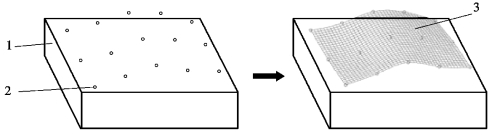
图7-17　全工作台热误差曲面建立过程

1.工作台；2.热误差预测值；3.热误差曲面

拟合和插值是两种常用的曲面建模算法，其区别在于插值建立的曲面是绝对通过所有离散点的，但建模算法较为烦琐，最终得到的模型形式也较为复杂，而拟合得到的曲面不能保证绝对通过所有离散点，但建模算法和模型形式也相对简单。

本节分别介绍一种拟合算法和一种插值算法。

1）多元回归曲面拟合

多元回归即利用残差平方和最小化思想，找到一个模型，使其对工作台上各点热误差的预测结果和对应位置点热误差模型预测结果之间残差的平方和达到最小。

根据工作台上各点测得数据组成的离散点判断曲面是否变化复杂，从而选取模型的阶数。考虑到机床机械部件的形体热变形是热源热量传递引起温度场变化导致的，机床结构庞大，热传递较为缓慢，因此整体的热变形呈渐变特性。曲面模型的阶数选取三阶进行建模，曲面模型形式如下：

其中，X 和Y 分别表示工作台上各点X 和Y 向的坐标，ΔEXY表示坐标对应点处的热误差值。曲面拟合的过程即求取上述模型参数a0，a1，…，a9 的过程。如果将上述模型视为线性模型，则自变量分别为：

假设工作台上P 个测点在某一时刻的热误差预测值分别为ΔE1，ΔE2，…，ΔEP，各测点的X 和Y 向坐标分别为X1，X2，…，XP 和Y1，Y2，…，YP。同样利用残差平方和最小的思想，建立多元回归曲面，如下所示：

其中

通常，拟合算法适用于整个曲面较为平缓，阶数不高的情况。当曲面变化较为复杂，存在局部的突变或者许多凹陷和凸起，说明整个曲面的阶数很高，如果采用强行高阶的函数进行拟合，会出现龙格现象，即整个曲面尤其是边缘位置存在剧烈的起伏波动，造成模型的稳定性急剧下降，此时，可采用插值算法，得到的结果要优于拟合。

2）B 样条函数曲面插值

插值的实质是将整个曲面分割成多个局部区域，利用多个低阶的基函数，分别对各个局部区域进行拟合，然后拼凑成整个曲面，拼凑时，需要注意各个局部区域边界的平滑性。对于阶数较高的曲面，可增加低阶函数的数量，进而在对曲面进行重构时，有效避免了龙格现象。B 样条函数曲面插值算法是常用的曲面插值算法，其基本原理如下。

B 样条函数曲面插值算法是一种将多个B 样条基函数进行加权叠加来重构曲面的技术。

B 样条基函数是一种表达多项式的函数形式，具体的函数需要依靠节点进行计算，节点是一组按从小到大顺序排列的数，比如[Xj，Xj+1]即构成了一组两个值的节点。可以用来定义B 样条函数Nj，0（X），如下。

其中Nj，0（X）的下标中的第一个j 表示B 样条函数对应的是节点中的第一个值，即Xj，第二个0 表示函数为0 阶的常数项函数。高阶的B 样条基函数可以通过多个0 阶的函数构成，计算方法如下：

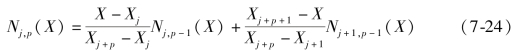
上式说明，如果要构建更高阶的基函数，需要两个低一阶的基函数，以及增加新的节点。结合式（7-23）和式（7-24）可以看出，只要节点确定了，基函数也随之确定。因此，在进行曲面插值时，对于构造基函数最重要的是确定节点。(www.xing528.com)

B 样条曲面由多个基函数加权组合而成，比如对于如图7-18 所示，在机床工作台上有矩形分布点阵。

其中，矩形点阵共有M 行和N 列，每一行的Y 向坐标分别记为Y1，Y2，…，YM，每一列的X 向坐标分别记为X1，X2，…，XN，每一个点对应一个热误差测量值，记为ΔEXjYi，据此建立的B 样条曲面形式如下：

其中Γi，j为权值，矩阵中每一个点都对应一个权值。比如位移坐标（X2，Y1）的点，对应的权值为Γ1，2。

式（7-25）说明，对于N 列不同X 坐标的点，需要构建N 个基函数Nj，p，j=1，2，…，N。对于M 行不同Y 坐标的点，需要构建M 个基函数Ni，p，i =1，2，…，M。

对于所有Nj，p其节点都一样，记为UX，如下

其中

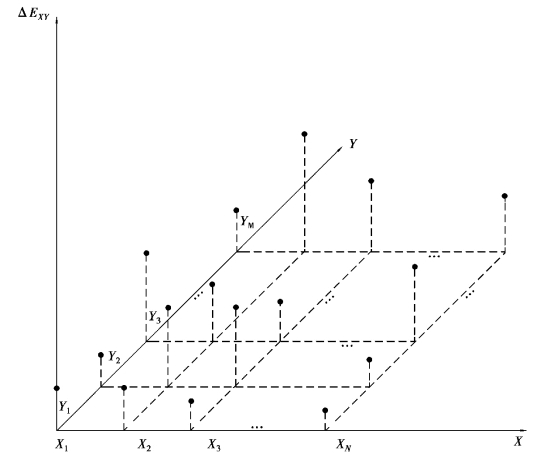
图7-18　矩形点阵

同理，对于所有Ni，p其节点都一样，记为UY，如下

其中

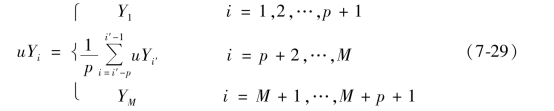
之后根据式（7-23）和式（7-24）即可计算出所有Nj，p和Ni，p。

对于上式（7-26） ～式（7-29），需要注意以下3 点：

①构造的节点会出现一样的值，在代入式（7-24）进行计算时，会出现分母为0 的项，如果出现，直接将此项等于0。

②对于X（Y）向最后一个基函数NN，p（NM，p），当把XN（YM）代入时，根据式（7-23）和式（7-24）计算得到值为0，因为式（7-23）判定为1 的条件为Xj≤X<Xj+1，不包含等于上界Xj+1的情况。进而会造成将XN 或YM 代入式（7-25）时计算得到的结果为0，无法等于热误差实测值。因此这种情况在计算式（7-23）时，需要强制将XN（YM）代入时的值设为1。

③对于阶数p，可以发现在构建节点时，需要将前p +1 和后p +1 个值进行设定，也就是说，节点的个数N+p+1 或M+p+1 至少要为2（p +1），据此可得：

也就是说，矩阵点的行数和列数至少要比阶数高1，否则无法计算。

式（7-25）中只剩权值Γi，j还未求出，对于M 行N 列，共有M ×N 个Γi，j。根据插值的定义，插值曲面是通过所有离散点的，即将图7-13 中任意点的坐标（Xj，Yi）代入式（7-25）中，计算的结果应该等于热误差的测量值ΔEXjYi。据此，可列出方程。

对于M ×N 个点，一共可以列出M ×N 个方程，并且方程中所有未知数Γi，j的最高次仅为1 次，因此，可以得到M ×N 个线性方程，求解即可得到所有Γi，j。

最后对于上述B 样条曲面插值，需要注意两点：

①上述方法只能插值矩形分布的点阵，如果点阵分布不规则，无法使用。

②无法对超出矩形点阵范围的区域进行插值，即插值使用范围为：