实切空转热误差特性比对分析

以Leaderway V-450 型数控机床Z 向热误差为例，探究实切和空转状态下热误差特性之间的差异。

1）实切热误差测量实验

实切状态下的热误差实验一共进行了3 批次，分别记为G1 ～G3，根据表6-6 所示的K1 ～K18 批次Z 向热误差温度敏感点选择结果，Z 向的温度敏感点只有T1 ～T5，因此所有批次实验初始温度测点为图6-1 和表6-1 中所示的T1 ～T10。在测量时，每3 分半钟测量一次，不同批次实验之间的进给速度和切削深度不同。

对于空转比对实验，选取环境温度接近的K3 ～K5 共3 批次进行比对。所有实验参数见表7-1。

表7-1　K3 ～K5，G1 ～G3 批次实验参数

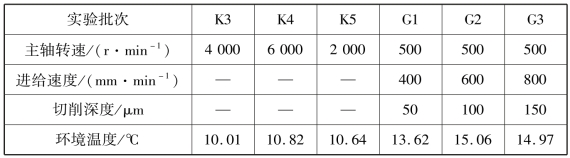
其中K3 批次和G1 批次实验测得的温度和热误差分别如图7-2 和图7-3所示。

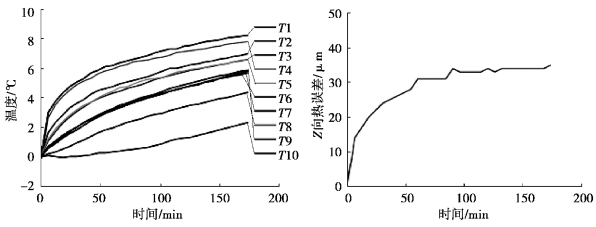
图7-2　K3（空转）批次温度（左）和热误差（右）测量数据

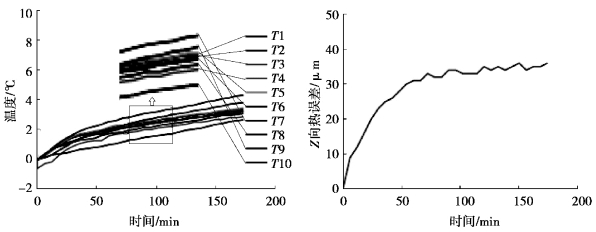
图7-3　G1（实切）批次温度（左）和热误差（右）测量数据

根据图7-2 和图7-3 可以看出空转和实切状态下机床各点温度和热误差的变化曲线存在明显差异，比如，空转状态下T1 温度测点变化最大，而实切状态则是T7。由此可见，机床在实际切削中，在处于不同工作模式下，随着切削力、冷却液等因素的增加，加之环境温度、机床本体结构、电机、加工材料属性、机床实切参数（如主轴转速）、切削深度、进给量等因素的综合耦合影响，使得热变形来源更加复杂，导致机床的温度场分布发生了变化。

为了进一步分析空转和实切温度场分布的差异，本著作采用FLUKE T1200 红外热像仪对机床温度场分布情况进行了监测，并对温度场分布变化进行了分析。数控机床在空转状态下达到稳定时的温度场分布（实验参数：转速4 000 r/min，稳定时间3 h）如图7-4 和图7-5 所示；在空转状态下达到稳定时的温度场分布（实验参数：转速1 500 r/min，稳定时间3 h）如图7-4 和图7-6 所示；在实切状态下达到稳定时的温度场分布（实验参数：转速1 500 r/min，进给量600 mm/min，切削深度100 μm，稳定时间3 h）如图7-4和图7-7 所示。

图7-4　数控机床温度场分布参照图

比对图7-5 和图7-6 可知，在空转状态、不同转速的情况下，机床温度场的温度数值发生了很大变化，但温度场分布规律未曾改变；比对图7-5 和图7-7可知，在空转和实切两种状态且不同转速条件下，机床的温度场在温度数值、温度场分布规律方面都发生了明显的变化；比对图7-6 和图7-7 可知，在空转和实切两种状态且相同转速条件下，机床的温度场在温度数值上差异不大，但温度场分布规律发生了明显的变化。由此直观地表明：在两种状态下，无论参数是否变化，机床温度场的分布规律都将会变化，从而在热误差建模时，非常可能引起温度敏感点的选择结果和最终的模型。

图7-5　机床在转速4 000 r/min 空转状态下的稳定温度场分布情况

图7-6　机床在转速1 500 r/min 空转状态下的稳定温度场分布情况

图7-7　机床在实切状态下的稳定温度场分布情况

2）建模及预测精度比对分析

分别根据K3 ～K5 和G1 ～G3 批次实验数据，建立空转和实切状态下的热误差模型，通过预测精度交叉比对分析空转和实切状态下热误差特性的差异。建模算法选择第3 章提出的强稳健性建模算法，选择两个温度测点作为温度敏感点，建立温度敏感点和热误差之间的预测模型。建模结果见表7-2。

表7-2　K3 ～K5，G1 ～G3 批次实验温度敏感点选择和建模结果

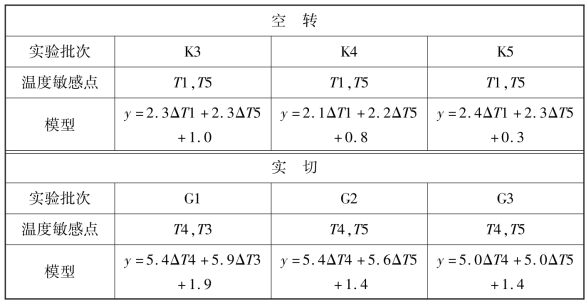
根据表7-2，机床空转和实切状态虽然工作模式不同，但各自的热误差补偿模型所依据的温度敏感点位置具备较好的稳定性，这也是模型稳健性的基础。同时，空转和实切状态下温度敏感点选择结果和最终建立的热误差补偿模型有明显的差异。温度敏感点从空转状态的T1，T5 变成T3，T4 或者T4，T5，说明实切状态下参数对机床温度场分布的影响，的确会引起热误差特性的变化，进而引起温度敏感点和热误差建模结果的不同。

预测精度交叉比对分析分为4 个部分，分别利用空转和实切实验数据建立的模型，对空转和实切状态下的热误差进行预测，比对空转预测空转，空转预测实切，实切预测空转和实切预测实切的预测精度，具体如下：

（1）通过空转数据建立的模型预测空转数据

分别利用K3 ～K5 批次空转实验数据建立的模型，将K3 ～K5 批次实验测量的温度值代入模型，反过来对K3 ～K5 批次数据进行预测，并计算残余标准差，记为，如式（7-1）。

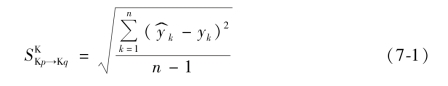(www.xing528.com)

其中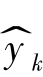 为Kp 批次数据建立的模型，将Kp 批次数据温度代入得到的预测结果，yk 为对应Kq 批次数据的测量结果。

之后对于每批次数据建立的模型，计算其对K3 ～K5 批次数据预测残余标准差的最大值，平均值和标准差，分别如式（7-2），式（7-3）和式（7-4）所示：

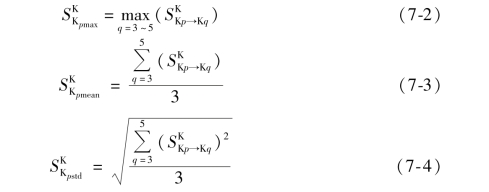
（2）通过空转数据建立的模型预测实切数据

分别利用K3 ～K5 批次空转实验数据建立的模型，将G1 ～G3 批次实验测量的温度值代入模型，对G1 ～G3 批次数据进行预测，并根据式（7-5）计算参与标准差，记为。

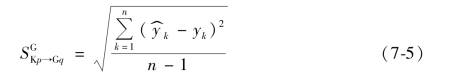
其中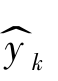为Kp 批次数据建立的模型，将Gq 批次数据温度代入得到的预测结果，yk 为对应Gq 批次数据的测量结果。

之后对于每批次数据建立的模型，计算其对G1 ～G3 批次数据预测残余标准差的最大值，平均值和标准差，分别如式（7-6），式（7-7）和式（7-8）所示：

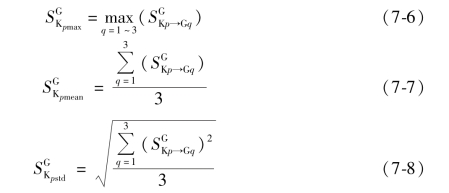
（3）通过实切数据建立的模型预测空转数据

分别利用G1 ～G3 批次空转实验数据建立的模型，将G1 ～G3 批次实验测量的温度值代入模型，对K3 ～K5 批次数据进行预测，并根据式（7-9）计算参与标准差，记为。

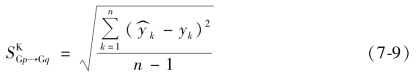
其中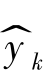 为Gp 批次数据建立的模型，将Kq 批次数据温度代入得到的预测结果，yk 为对应Kq 批次数据的测量结果。

之后对于每批次数据建立的模型，计算其对K3 ～K5 批次数据预测残余标准差的最大值，平均值 和标准差，分别如式（7-10），式（7-11）和式（7-12）所示：

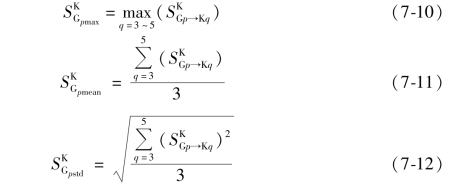
（4）通过实切数据建立的模型预测实切数据

分别利用G1 ～G3 批次空转实验数据建立的模型，将G1 ～G3 批次实验测量的温度值代入模型，反过来对G1 ～G3 批次数据进行预测。并根据式（7-13）计算参与标准差，记为。

其中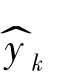为Gp 为批次数据建立的模型，将Gq 批次数据温度代入得到的预测结果，yk 为对应Gq 批次数据的测量结果。

之后对于每批次数据建立的模型，计算其对G1 ～G3 批次数据预测残余标准差的最大值，平均值 和标准差，分别如式（7-14），式（7-15）和式（7-16）所示：

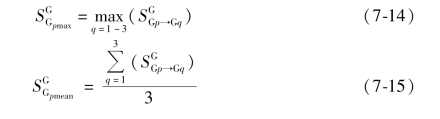
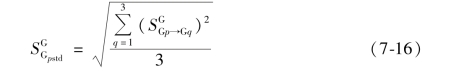
预测精度交叉比对分析结果分别如图7-8，图7-9 和图7-10 所示。

图7-8、图7-9 和图7-10 中的横坐标为模型建立对应的实验批次，纵坐标为模型的预测结果。明显可以看出，相对于空转预测空转、实切预测实切，空转预测实切、实切预测空转的误差明显偏大，说明空转状态和实切状态的热误差特性存在着明显差异，并且这种差异已经对模型的预测精度产生了实质性的影响，对于实际加工来说，利用实切状态下测量数据建立的模型会更加合适。

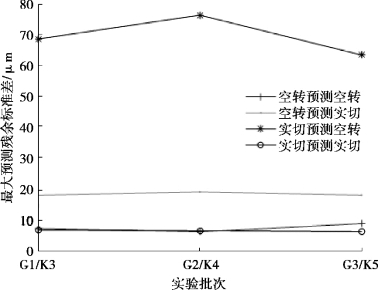
图7-8　空转实切热误差预测精度交叉比对分析——残余标准差最大值

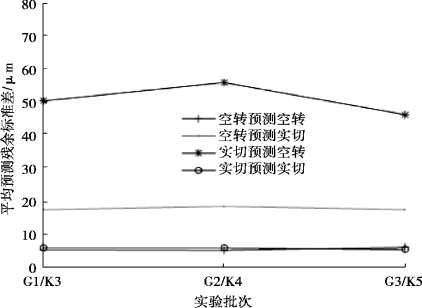
图7-9　空转实切热误差预测精度交叉比对分析——残余标准差平均值

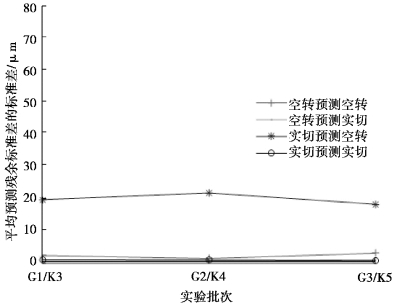
图7-10　空转实切热误差预测精度交叉比对分析——残余标准差的标准差