神经网络结构比对及热误差预测精度验证

建模算法的好与坏需要依靠对热误差的实际预测精度来比对，才具有说服力。为了验证上述3 种“RRR method”“PCRR method”和“SUERR method”对热误差预测精度和预测稳健性的提升效果，本著作利用K1 ～K18 批次实验数据，同样以Z 向为例，将其与目前常用的多元回归和神经网络建模的方法进行比对。两种参与比对的方法均采用模糊聚类结合灰色关联度法选择温度敏感点，第一种方法采用多元线性回归算法建立热误差模型，本著作称之为“传统多元线性回归热误差建模方法”，简称“TMLP method”；第二种方法采用神经网络算法建立热误差模型，本著作称之为“传统神经网络热误差建模方法”，简称“TNN method”。具体所有参与比对的算法如下：根据神经网络的原理可知，神经网络建模之前，首先需要确定神经网络的结构，即选择合适的隐藏层数和每一层的节点数，以及每一层节点的转移函数类型，以使得神经网络模型具有最优的预测精度和稳健性。对此，许多研究人员都提出了对神经网络的优化方法，比如蚁群算法（ACO-NN）、遗传算法、贝叶斯理论等。这些方法实质上是一种搜寻算法，基于实验数据来验证不同结构神经网络的预测效果，直到找出满意的神经网络优化结构。所以，其建立的神经网络模型的精度和稳健性依赖于用于优化的实验数据量，如果要建立稳健性好的热误差补偿模型需要进行大量长期实验，在工程应用中是无法接受的。所以本著作选择直接借鉴之前研究者采用的神经网络结构用于“TNN method”中的神经网络建模算法。经过调研，在提到具体结构的神经网络热误差建模文献中，Y.Zhang 比对了两种神经网络结构，都采用了一层隐藏层，转移函数都为sigmoid，只不过两种结构的节点数分别为4 和6，经过实验验证两种结构都具有良好的效果。R.J.Liang 比对了3 节点隐藏层神经网络和15 节点隐藏层神经网络，结果发现3 节点隐藏层的热误差预测效果较好。J.Yang 采用5 节点隐藏层神经网络建立热误差补偿模型。经过总结，发现在热误差建模中，多采用1 层隐藏层，3 ～6 个隐藏层节点结构，并且采用sigmoid 作为转移函数。故本著作决定采用1 隐藏层，4 隐藏层节点的神经网络结构，并采用sigmoid 函数作为隐藏层转移函数。考虑到sigmoid 函数的值域介于0 和1 之间，小于热误差的变动范围，本著作在输出层采用pureline 转移函数，对隐藏层输出进行线性变换。

K1 ～K18 批次数据Z 向热误差建模结果比对见表6-7。

表6-7　K1 ～K18 批次数据Z 向热误差建模结果比对

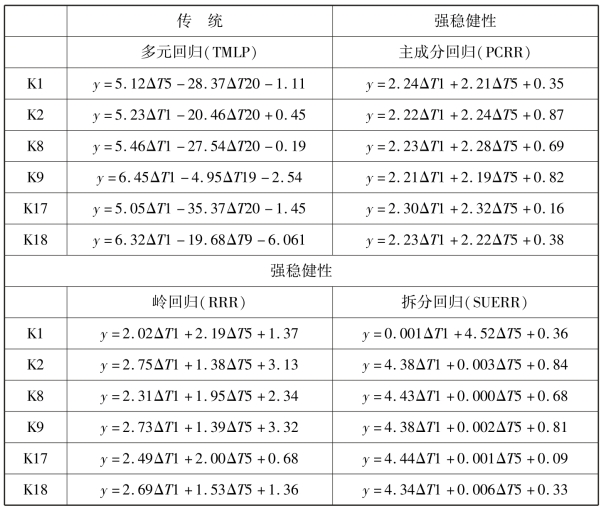
对于表6-7，碍于篇幅，每种模型仅展示6 批次实验结果，并且由于神经网络模型结果为网络节点结构，难以表达，因此对于传统建模算法仅展示多元回归模型结果。从表6-7 可以看出，传统建模算法得到的模型系数波动性很强，这是因为和热误差关联性较弱的温度敏感点随着时间的增长，和热误差之间的关联特性发生改变导致的。而强稳健性建模算法得到的模型系数非常稳定，规律也很明显，即两个温度敏感带系数相加结果在4.2 ～4.6 变化，这说明机床上存在温度敏感点，在相应条件下能够和热误差保持稳定关联性。

残余标准差是目前常用的热误差预测精度评价指标，分别利用各批次数据建立的模型，将K1 ～K18 批次实验测量的温度值代入模型，反过来对K1 ～K18 批次数据进行预测，并参考式计算残余标准差，记为SKp→Kq。计算方法如下：

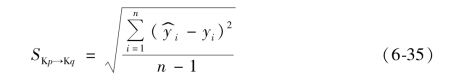
其中为Kp 批次数据建立的模型，将Kq 批次数据温度代入得到的预测结果，yi 为对应Kq 批次数据的热误差测量结果。

之后对于每批次数据的每个模型，分别计算其对K1 ～K18 批次数据预测残余标准差的最大值SKpmax，平均值SKpmean和标准差SKpstd，分别如式（6-36），式（6-37）和式（6-38）所示：(www.xing528.com)

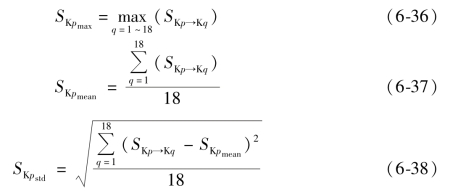
其中最大值SKpmax和平均值SKpmean表示模型预测误差的大小，反映了模型算法的精度，标准差SKpstd表示模型算法在应用于不同批次数据中预测精度的波动情况，反映了模型的稳健性，计算结果分别如图6-20，图6-21 和图6-22所示。

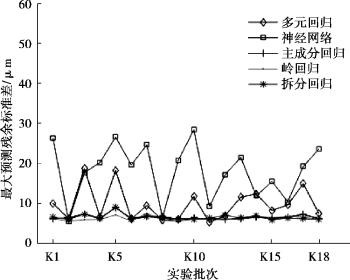
图6-20　预测残余标准差最大值

图6-21　预测残余标准差的平均值

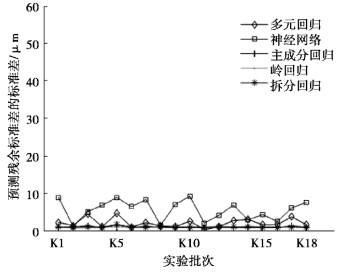
图6-22　预测残余标准差的标准差

根据图6-20 至图6-22 可以看出，无论是最大值、平均值还是标准差，传统建模算法在应用于K1 ～K18 批次数据时出现了剧烈的波动，而强稳健性建模算法预测误差波动较小，并且整体预测误差明显小于传统算法，各批次数据建立模型的预测残余标准差最大值不超过10 μm。说明强稳健性建模算法能够将机床温度和热误差之间的规律准确地提取出来，从而不仅具有较高的预测精度，稳健性也得到了大幅提升。