主成分回归算法核心思想是降维,多个自变量之间如果具有很强的共线性,说明其包含的信息存在很高的重复性,主成分回归将所有变量的测量值通过某种特定的线性组合转换成新的正交向量,进而在建模之前,首先对所有正交向量信息量进行筛选,将信息量较少的向量剔除,留下包含主要信息且相互正交的向量,即主成分。正交即意味着不具有共线性,因此采用主成分进行回归建模,也可以有效抑制共线性对模型的干扰,回归之后,再通过反线性变换,将主成分还原为模型的自变量即完成建模。具体说明如下。
如图6-19 所示,假设两个自变量x1 和x2,其之间具有很强的共线性,画出两个变量的测量值。

图6-19 主成分回归算法原理
图6-19 中,分别将x1 和x2 视为坐标系的两个坐标轴,然后根据测量数据,做出x2 随x1 的变化散点图,可以发现,其之间呈很强的线性变化关系。但如果通过变换,将x1 和x2 转换为新的变量z1 和z2,如下:

并在变换的过程中,去掉z1 和z2 之间的关联性,则会得到两个完全不具备共线性的自变量,即主成分变量。利用主成分变量,再进行回归即可消除共线性对模型精度的影响。另外,根据图6-19 可以看出,两个主成分变量包含的信息量完全不同,当z1 逐渐增大时,z2 仅在0 附近小范围波动。因此,在建模时去掉z2,仅保留包含主要的信息z1。这样做有利于进一步消除数据中噪声信息对模型精度的干扰。
主成分回归建立的模型如下:
![]()
最后结合式(6-11)和式(6-12)将z1 展开,得到最终关于x1 和x2 的建模结果,如下:
![]()
基于上述原理,主成分建模分为下面几个步骤。
(1)标准化数据
对于m 个自变量x1,x2,…,xm,首先进行预处理,如下:

其中xi1为变量xi 的第一个测量值,STDxi 为变量xi 的标准差,计算方法见式(5-5)。
处理过后,原自变量x1,x2,…,xm 变成![]() 。
。
(2)提取主成分变量
对于m 个新自变量![]() ,求其协方差矩阵COV。
,求其协方差矩阵COV。
![]()
其中covi,j为变量 和
和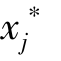 之间的协方差,计算方法如下:
之间的协方差,计算方法如下:
![]()
其中,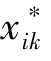 和
和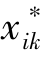 为变量
为变量 和
和 的第k 个测量值,MNx∗i 为变量
的第k 个测量值,MNx∗i 为变量 的平均值,计算方法见式(5-6)。
的平均值,计算方法见式(5-6)。
提取COV 的特征值和特征向量,分别记为λ1,λ2,…,λm 和P1,P2,…,Pm。

其中特征值和特征向量为使COV 满足以下关系的数和向量。(https://www.xing528.com)
![]()
特征值和特征向量的个数和COV 的阶数相等,即和自变量的个数相等。
之后提取主成分变量,记为z1,z2,…,zm,方法如下:
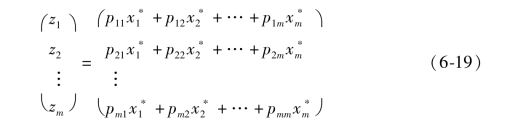
(3)筛选主成分变量
对于主成分变量z1,z2,…,zm,其通过特征向量计算得到,将每个特征向量对应的特征值按从大到小的顺序进行排序,假设排序后λ1 >λ2 >…>λm。
则每个特征值的大小反映了对应主成分变量包含的信息量,即信息量z1 >z2 >…>zm。
保留前g 个使信息量累计贡献率Vccg 大于85%的主成分变量z1,z2,…,zg。Vccg 计算方法如下:

(4)建立主成分变量回归模型
设因变量为y,同样根据式(6-14)进行标准化处理,处理后的数据记为y∗。通过多元回归建立y∗关于z1,z2,…,zg 的模型,如下:
![]()
其中:

其中y∗为变量y∗所有测量值组成的列向量,z=(z1,z2,…,zg),zi 为变量zi 所有测量值组成的列向量。
(5)变换得到最终建模结果
结合式(6-22)和式(6-19),得到将变量z1,z2,…,zg 展开y∗关于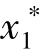 ,
,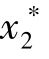 ,…,
,…, 的模型,如下:
的模型,如下:
![]()
令:
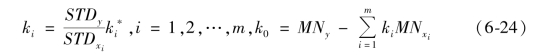
其中MNy 和STDy 分别为变量y 的平均值和标准差,计算方法分别如下:
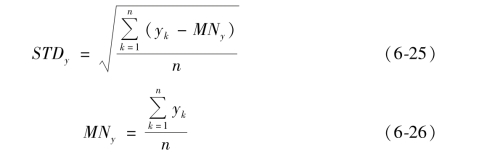
最终得到因变量y 关于自变量x1,x2,…,xm 的主成分回归模型,如下:
![]()
为了便于后文描述,将利用主成分回归建立模型的方法称为“数控机床热误差补偿主成分回归稳健性建模方法”,简称“PCRR method”。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




