相对于式(6-6)所示的多元线性回归算法模型系数估计式,A.E.Hoerl 提出的岭回归算法对模型系数估计式如下:
![]()
其中,k 为岭参数,且k≥0,I 为单位矩阵。从式(6-9)中,可以看出,岭回归算法给XTX 加上一个正常数矩阵kI,放弃了对模型系数的无偏估计,即图6-13 中所示的模型系数估计值出现的最大概率不等于真实值。但是也减小了共线性导致的XTX 接近奇异矩阵的程度。此时,模型系数的方差如式(6-10)所示:
![]()
通过比对式(6-6)和式(6-9)不难发现,通过合理的增大岭参数k,可以使XTX 偏离奇异矩阵,A.E.Hoerl 发现,这种做法可以在模型系数估计值最大概率位置并且在极小偏离真实值的情况下,大幅减小模型系数估计值的方差。在模型输入变量存在严重共线性时,由于方差较小,使得模型系数接近真实值的概率大幅增加,从而抑制了共线性对模型系数估计值的影响,提升模型的预测精度和预测稳健性。
但是,在建立岭回归模型之前,必须要确定合理的岭参数k 值,如果无限制地增大岭参数,最终也会引起模型系数估计值偏离真实值增大到无法容忍的程度,所以,结合K1 ~K18 批次数控机床热误差实验数据,对岭参数k 值进行了选择。
本著作将岭参数k 值逐渐由0 顺序递增,直到k =25,分析不同k 值时模型的预测精度和预测稳健性,以寻找出最佳岭参数进行建模。以K1 批次数据主轴Z 轴向热误差为例,具体步骤如下。
①将k 取值从0 开始,每次增加0.1,直到k=25。
②对于每个k 取值,根据式(4-6)建立热误差模型,并对其余批次数据进行预测,计算预测残余标准差S。
③分别计算各批次数据预测标准差的平均值,用于表征预测精度,计算各批次数据预测标准差的标准差,用于表征预测稳健性。
④预测标准差的标准差和平均值随岭参数变化如图6-13 所示。
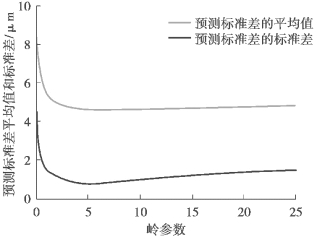
图6-13 K1 批次Z 向热误差预测效果随岭参数变化轨迹(https://www.xing528.com)
⑤根据图6-13 可见,当岭参数大于一定值后,预测效果趋于稳定。同样的情况也出现在Y 向热误差中,由于数据量过大,无法一一呈现,所以仅选择具有代表性的K1、K9、K18 三批次数据。图6-14 为K1 批次Y 向热误差预测效果随岭参数变化情况;图6-15、图6-16 为K9 批次Y 向、Z 向热误差预测效果随岭参数变化情况;图6-17、图6-18 为K18 批次Y 向、Z 向热误差预测效果随岭参数变化情况。
从图6-13—图6-18 可以看出,当岭参数大于20 后,预测效果和模型系数随着岭参数的继续增大趋于平稳。因此,对于本著作参照研究的数控机床进行的热误差建模,将式(6-9)中的岭参k 值取20 较为合适。为了便于后文描述,将利用相关系数选择温度测点,利用岭回归建立模型的方法称为“数控机床热误差补偿岭回归稳健性建模方法”,简称“RRR method”。
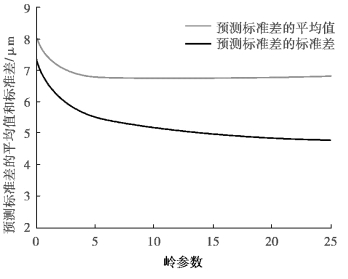
图6-14 K1 批次Y 向热误差预测效果随岭参数变化轨迹
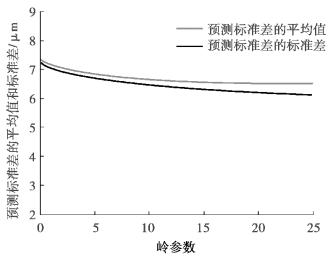
图6-15 K9 批次Y 向热误差预测效果随岭参数变化轨迹
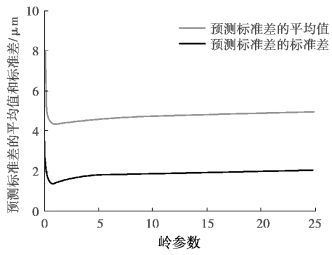
图6-16 K9 批次Z 向热误差预测效果随岭参数变化轨迹
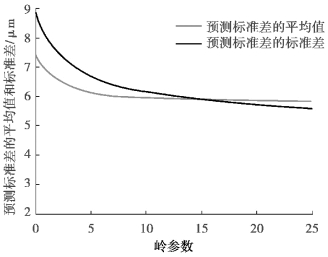
图6-17 K18 批次Y 向热误差预测效果随岭参数变化轨迹
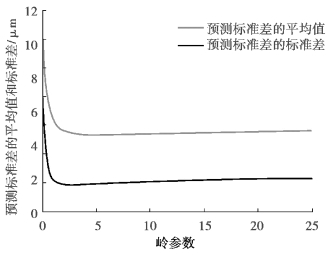
图6-18 K18 批次Z 向热误差预测效果随岭参数变化轨迹
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




