实验结果的分析和优化方案

通过模糊聚类结合灰色关联度算法对于温度敏感点选择的结果（优先考虑减小共线性），以及直接利用灰色关联度对于温度敏感点选择的结果（优先考虑提升关联性），对温度敏感点之间共线性与温度敏感点和热误差之间关联性的矛盾关系进行了说明。

以Z 向热误差测量数据为例，根据上述K1 ～K18 批次实验数据，采用模糊聚类结合灰色关联度算法对温度敏感点进行选择，比如对于K1 批次数据，首先利用模糊聚类算法对T1 ～T20 共20 个温度测点进行分类，结果见表6-3。

其次计算各温度测点和Z 向热误差的灰色关联度，结果见表6-4。

表6-3　K1 批次温度数据模糊聚类分类结果

表6-4　K1 批次各温度测点与Z 向热误差灰色关联度

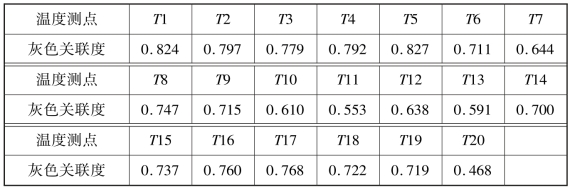
最后从各类中选择灰色关联度最大的温度测点作为温度敏感点，即T5和T20。

同理，对K2 ～K18 批次Z 向热误差温度敏感点进行选择，并将K1 批次选择的温度敏感点合并，结果见表6-5。

在表6-5 中，每批次数据选出的温度敏感点组合都包含T1 和T5，以T1为主，少数情况会出现T5，而另一温度敏感点则包含T7，T8，T9，T10，T12，T17，T19，T20。可见，通过模糊聚类结合灰色关联法选出的温度敏感点，随着天气季节变化，位置也随之波动变化，本著作称此种现象为“温度敏感点变动性”。为了究其原因，对温度敏感点之间的共线性、温度敏感点和热误差之间的关联性进行分析。

表6-5　K1 ～K18 批次数据模糊聚类结合灰色关联法温度敏感点选择结果

分别计算表6-5 中Z 向热误差温度敏感点之间的方差膨胀因子（VIF），来衡量共线性温度敏感点之间的共线性程度，结果如图6-9 所示。

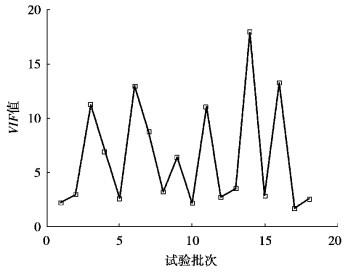
图6-9　K1 ～K18 批次数据Z 向热误差温度敏感点之间VIF 值

根据共线性计算结果，可以看出，温度敏感点之间VIF 值基本不超过10，说明模糊聚类算法的确能够起到良好的共线性减小作用。(www.xing528.com)

之后，对K1 ～K18 各批次数据温度敏感点的灰色关联度进行排序。以分析温度敏感点和热误差之间的关联性，比如对于K1 批次数据，根据表3-4，对各温度测点和热误差之间灰色关联度的大小顺序进行排序

即T5 的灰色关联度在20 个温度测点中是最大的，排序为1，T20 是最小的，排序为20。

同理，对其他各批次数据Z 向热误差进行同样的分析，温度敏感点灰色关联度排序如图6-10 所示。

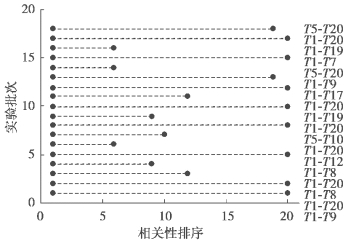
图6-10　K1 ～K18 批次数据Z 向热误差温度敏感点灰色关联度排名

根据图6-10 的排名结果可以看出，每批次实验根据模糊聚类结合灰色关联度算法选择的2 个温度敏感点中，其中一个与热误差之间的灰色关联度排序最靠前，而另一个非常靠后。说明传统温度敏感点选择算法，仅能选取一个与热误差关联性较大的温度敏感点，而另一个温度敏感点和热误差之间的关联性较弱。这是由于机床的温度在热传导过程中，存在极强的耦合作用，导致与热误差关联性强的温度测点全部集中于主要热源附近，其之间的共线性也随之增强。必然出现这些强共线性的温度测点被归为一类，因此，要利用模糊聚类优先减小温度测点之间的共线性，使其中只能有一个被选为温度敏感点。在减小共线性的同时，另外的温度敏感点所在分类，也牺牲了温度敏感点和热误差之间的关联性。和热误差之间关联性较弱的温度敏感点，在长时间跨度范围，往往难以保持与热变形具有强关联性，正因为这个原因，温度敏感点非但无法为热误差预测提供长期稳定的有效信息来源，反而容易受到与热误差不相关的热源干扰，引入额外的误差影响因素，出现变动性，最终会导致预测精度的下降。

如果在选择温度敏感点时，不再考虑减小共线性，即跳过模糊聚类的步骤，直接利用灰色关联度计算各批次数据所有温度测点和热误差之间的关联性，然后选出两个关联性最强的温度测点作为温度敏感点，K1 ～K18 批次实验数据选择结果见表6-6。

表6-6　K1 ～K18 批次实验Z 向热误差灰色关联度直接选择温度敏感点结果

之后同样利用方差膨胀因子（VIF），来衡量温度敏感点之间的共线性，并和传统模糊聚类结合灰色关联度算法选出的温度敏感点共线性进行比对，结果如图6-11 所示。

对比表6-6 直接根据灰色关联度选择的温度敏感点，和表6-5 根据模糊聚类结合灰色关联度选择的温度敏感点可以发现，直接选择的温度敏感点恒定在T1 和T5，变动性明显降低，表明选出的温度测点可以保持和热误差之间长期稳定的关联性，有利于热误差的长期预测的稳健性。但同时比对图6-9和图6-11，即观察两种方法选出温度敏感点之间的共线性，可知直接选择两个强关联性的温度敏感点之间出现了极高的共线性。从数学角度分析，这会导致多元回归等算法在建模过程中，极度放大输入变量测量值中误差的干扰，导致建立的模型对输入数据变动量异常敏感，模型预测稳健性较差。

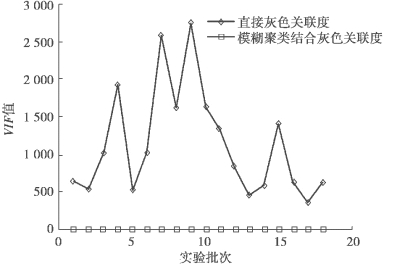
图6-11　两种算法温度敏感点共线性比对

综上，温度敏感点之间的共线性和关联性存在矛盾，无法在减小温度敏感点之间共线性的同时，保证温度敏感点和热误差之间的关联性。