神经网络算法优化技巧

相对于多元回归，神经网络在非线性模型的处理上有优势，理论上，神经网络可以拟合出任意复杂形状的曲线。并且，如果模型建立后，又得到新的建模数据，神经网络作为一种学习算法，重新更新模型较为简单，而多元回归模型只能结合之前建模所用的数据重新建模。但神经网络也有其弊端，在下文会进行介绍。

神经网络模型从形式上是节点构成的网络状结构，包括输入层、隐藏层和输出层，如图5-6 所示。

图5-6　神经网络模型结构形式

图5-6 中所示的神经网络，输入层有两个节点，说明模型有两个输入变量；有一个输出层节点，说明模型有一个输出变量。也就是说，模型的输入层和输出层节点数由输入变量和输出变量决定。隐藏层可以有多层，且每一层的节点数可以不一样。对神经网络的结构优化主要就是指对隐藏层的层数和每层的节点数进行合理的选择。

神经网络节点的工作原理如图5-7 所示。

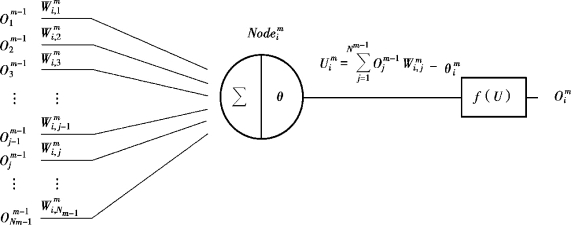
图5-7　神经网络节点工作原理

在图5-7 中，示意了一个位于m 层的节点，工作时，其首先对上一层节点的输出，…，按照权值进行加权求和，并减去阈值得到活化值，之后代入转移函数f（U）求取节点的输出，传给下一层节点，直至到达输出层。

其中，Nm-1指m-1 层节点的个数。

通常，每一层的节点具有相同的转移函数，且常用的转移函数有sigmoid、tanh 和pureline 3 种形式，分别如下所示：

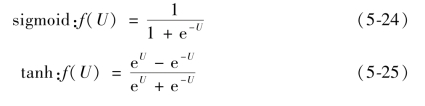
利用神经网络进行建模的过程其实就是对节点权值和阈值进行调整的过程。

根据式（5-18），将输入变量实际测量值代入神经网络得到的输出值与输出变量的实际测量值进行比较，可以求得残差平方和E，进而根据式（5-19），E也是关于神经网络中所有参数的函数，只不过对于神经网络，参数变成了网络中每个节点的权值 以及阈值。如果对E 关于所有连接权值和阈值求全微分，可得

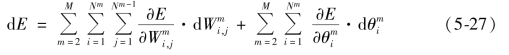
其中，M 为神经网络的层数，仔细观察式（5-27），可以发现求全微分时，是从第二层）开始的，即忽略了作为第一层的输入层，这是因为通常在输入层不设置权值和阈值，输入变量直接传给下一层。

如果对于每一次调整神经网络的参数时，令权值和阈值的调整量分别如下：

(www.xing528.com)

其中，和分别为权值和阈值调整量，η 为学习速率。

分别将式（5-28）和（5-29）代入式（5-27），即可求出则每次调整之后，残差平方和E 的变化量，如下所示：

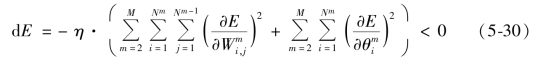
其中，dE 为每次参数调整E 的变化量，η 越大，E 每次调整时的变化越大。

根据式（5-30），可见每次调整，E 的变化总是向负方向变化，但同时E 作为平方和项，是一定大于0 的，因此，神经网络的每一次调整，都是向着残差平方和减小的方向。如果不断按此方法调整神经网络中的参数，则会使残差平方和不断减小，最终减小到可接受范围内，即认为完成建模。

本节最后解释一下神经网络建模中，著者认为容易陷入误区的地方。

①根据式（5-30）的解释，可能有研究人员会产生疑问：如果无限次数调整神经网络，会不会使E 最终小于0？

E 作为平方和的形式，是不可能小于0 的。其实，对于式（5-30），dE 小于0 是有前提的，即在当前网络参数附近的小范围内能够保证，如图5-8 所示。

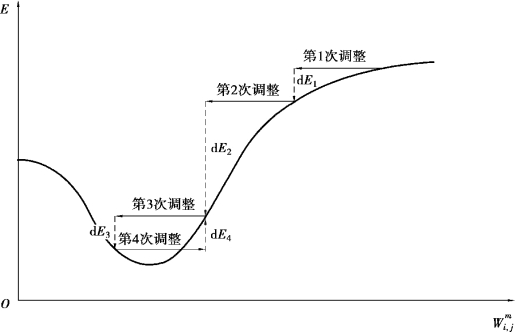
图5-8　残差平方和变化过程

图5-8 所示为残差平方和E 随某一节点权值的调整而变化的过程，对于每次参数调整的方向，实际上是以当前参数点作为参考的，比如，第4 次调整时，根据参数调整之前的起点位置，可以看出向横坐标正方向调整会减小残差平方和，但是当调整量过大，E 略过极小值后，继续调整反而增大了E。因此，神经网络并非调整次数越多，E 越会无限减小。

②为什么不和多元回归一样，仿照式（5-22），直接列方程求解使残差平方和处于最小的网络参数？

首先观察式（5-24）和式（5-25）所示的非线性转移函数，其形式较为复杂，加上神经网络节点传递的累加，最终形成的函数形式非常复杂，导致列方程式极为困难。另外对于非线性神经网络，其残差平方和E 不止有1 个极小值，如图5-9 所示。

如图5-9 所示，随着网络参数的变化，残差平方和E 存在一个最小值，但同时，也会在多个地方出现局部极小值，理论上这些局部极小值也满足方程（5-22），因此列方程是无法直接求解的。

其实，神经网络在接近某一局部最小值后，是不会跳出来的，比如，图5-8如果存在第5 次调整，理论上会向着横坐标负方向，当调整再次略过极小值后，会再次向横坐标正方向调整，此现象称为陷入局部极小值。而神经网络能否到达真正的全局最小值，全凭神经网络调整之前的初始参数分布。因此，这是神经网络采用非线性转移函数造成的一个很大的弊端，也是一个研究的热点。

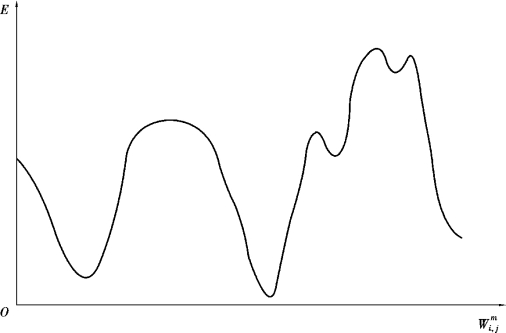
图5-9　残差平方和大范围变化过程

如果对于所有节点，均选择式（5-26）所示的线性转移函数，则神经网络其实就是多元线性回归，对于同样的测量数据，两种建模算法能够得到完全一模一样的结果，此时神经网络也不再具备非线性拟合上的优势。

热误差建模并非算法越复杂越好，模型稳健性、优劣性是由模型所表达的变化规律与现实热误差变化规律的符合程度来决定的，也就是模型与误差规律的契合度大小。对于热误差建模，热误差和温度之间基本是线性相关，而神经网络算法的非线性优势在此并不突出；此外，在模型应用补偿后，无法实现在机床运转时同时实时获得热误差和温度的测量值，也就难以发挥神经网络在模型在线更新修正上的优势。因此，本著作建模倾向于根据数控机床实际工况误差变化规律，选用合理的算法建立热误差补偿模型，模型优劣的评估应在于模型契合度状态。