残差平方和最小化思想是工程中常用多元回归建模算法的核心思想,原理如下。
如果将模型视为一个函数,则函数的输出由代入函数的自变量和函数中包含的系数共同决定。假设现在有一个函数,包含1 个因变量和m 个自变量,如式(5-15)所示。
现有一组所有上述函数自变量和因变量的测量值,分别记为y0 和X0,如式(5-16)所示。
其中,n 为每组测量值的长度,显然,如果将X0 带入式(5-15)中,无论函数的系数是多少,总能求出一组因变量的函数输出值,不妨记为 ,如式(5-17)所示。
,如式(5-17)所示。
 越接近y0,说明函数对数据中蕴含规律的表达越准确,残差平方和即用于描述
越接近y0,说明函数对数据中蕴含规律的表达越准确,残差平方和即用于描述 和y0 之间的接近程度,如式(5-18)所示。
和y0 之间的接近程度,如式(5-18)所示。
其中E 为残差平方和,通过对 和y0 每个测量值之间差值进行平方求和计算得出,E 越小,说明
和y0 每个测量值之间差值进行平方求和计算得出,E 越小,说明 越接近y0。
越接近y0。
当函数中系数发生改变,会引起 的变化,进而引起E 的变化。也就是说,E 和函数系数也存在一个对应的函数关系,如式(5-19)所示。
的变化,进而引起E 的变化。也就是说,E 和函数系数也存在一个对应的函数关系,如式(5-19)所示。
其中,k0,k1,k2,…,kl 为式(5-15)所示函数包含的系数,残差平方和最小化的建模思想即找到一种系数的组合,使E 达到最小值。基于此思想,多元回归和神经网络等算法均为常用的求解算法。(https://www.xing528.com)
多元回归将待建立的模型视为线性多项式形式,比如:
当模型为非线性时,可以通过一定的变换成线性形式,比如:
只要将x1、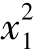 、ln x1 分别视为模型的3 个自变量,则模型依然呈线性多项式形式。
、ln x1 分别视为模型的3 个自变量,则模型依然呈线性多项式形式。
通过求取偏导数的零点可以求出函数的极值点,根据式(5-18)可以看出,残差平方和不存在最大值,因此,只要残差平方和关于模型系数的函数(式(5-19))有极值点,并且唯一,则肯定是残差平方和极小值点。进而,求取式(5-19)的偏导数零点,可以列出以下方程:
方程具体的求解过程本节不再详述,求解的结果如下所示。
其中,XC =(1 X0) =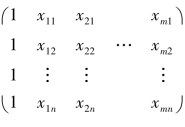 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




