灰色系统理论相关性计算算法概述

温度敏感点的相关性是指温度敏感点和热误差之间的关联程度，相关性越强，表明温度敏感点与热误差之间的联系越紧密，有利于增强模型的精度和稳健性。如果采用相关性较弱的温度敏感点进行建模，敏感点和热误差之间的关联特性很容易随着外界条件的变化而改变。在预测时，模型会输出和热误差规律完全不相符的预测值，不仅不会提升热误差补偿模型的预测精度，反而会成为干扰项，造成模型稳健性的下降。

灰色关联度是热误差建模领域中最常用的判断温度测点和热误差之间相关性的算法。

灰色系统理论提出了对各子系统进行灰色关联度分析的概念，通过一定的方法，寻求系统中各因素之间的数值关系。简言之，灰色关联度分析的意义是指在系统发展过程中，如果两个因素变化的态势是一致的，即同步变化程度较高，则可以认为两者关联较大；反之，则两者关联度较小。采用邓氏关联度计算公式，即

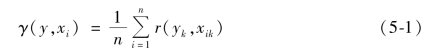
式（5-1）中，y 代表即热误差，xi 代表为第i 个温度测点观测值，yk，xik分别代表热误差和第i 个温度测点的第k 个观测值，γ（y，xi）为热误差和第i 个温度测点之间的灰色关联度，由各个观测值的关联度γ（y，xi）平均而来。γ（y，xi）计算公式如下

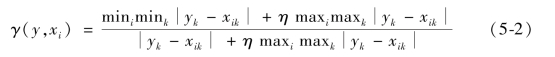
其中　η——分辨系数，η∈[0，1]，一般取η=0.5。

灰色关联度的计算结果在[0，1]，灰色关联度越高，说明两变量之间的关联程度越强。

在计算灰色关联度之前，必须要首先进行初始化处理，否则就会出现计算结果不准确情况，具体如下：

观察式（5-2），如图5-1 所示。

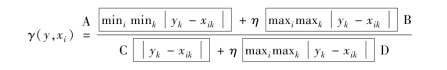
图5-1　灰色关联度计算公式剖析

从图5-1 中可以发现，各个观测值的关联度共有A，B，C，D 4 部分构成，其中A，B，D 部分对于所有观测值的关联度计算来说，都是常数，所以真正能够引起灰色关联度变动的只有C 部分。C 部分实质为热误差和第i 个温度测点在第k 个观测值的差，C 越小，表明温度测点和热误差变化曲线越接近，即灰色关联通过变量变化曲线的几何相似程度来判断温度测点和热误差之间的相关性。这种做法的好处在于对于处理非线性数据仍然有着良好的适应能力，但同时也导致了一个问题，如图5-2 所示。

在图5-2 中，3 条曲线分别代表了3 个变量随时间变化的结果，每个变量均有6 个测量值，对于变量1，很明显变量3 与其有着很明显的关联性，即2 倍关系，而变量2 和变量1 无任何关系。下面分别根据3 个变量的测量值，计算变量1 和变量2、3 之间的灰色关联度，将变量1 视为y，分别将变量2、3 视为x1 和x2。

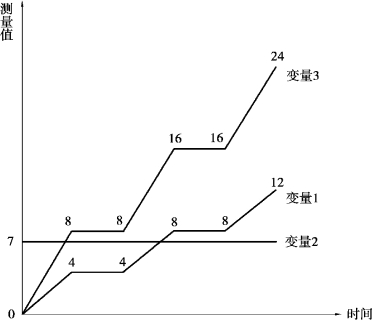
图5-2　量纲对灰色关联度影响

首先计算图5-1 所示的公式（5-2）A 部分，如下所示：

之后计算图5-1 所示的公式（5-2）B 部分，如下所示：

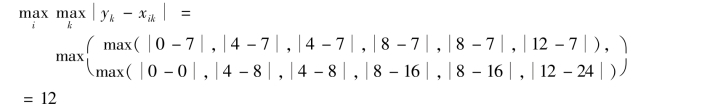
计算变量1 和变量2 之间的灰色关联度，如下所示：

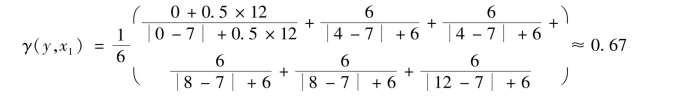
计算变量1 和变量3 之间的灰色关联度，如下所示：

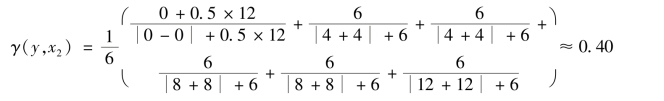
计算结果显示，变量1 和变量2 之间的灰色关联度要明显高于变量1 和变量3，显然和客观事实不符。

此问题是灰色算法原理本身导致的，没有考虑变量量纲的影响。因此，在计算灰色关联度之前，需要对变量进行无量纲化处理，常用的处理算法主要包括以下4 种。

（1）总和标准化

分别求出各变量测量数据的总和，之后用各测量值除以总和，得到无量纲处理后的数据。如式（5-3）所示。

（2）标准差标准化(www.xing528.com)

分别求出各变量测量数据的标准差，之后用各测量值除以标准差，得到无量纲处理后的数据，如下所示：

其中：

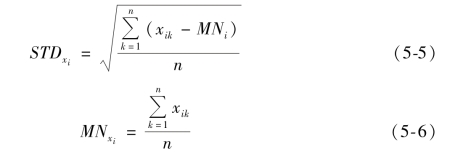
（3）极大值标准化

分别求出各变量测量数据的极大值，之后用各测量值除以极大值，得到无量纲处理后的数据，如下所示：

（4）极差标准化

分别求出各变量测量数据的极差，即极大值减去极小值，之后用各测量值减去极小值，再除以极差，得到无量纲处理后的数据，如下所示：

上述标准化的处理算法会造成应用时难以统一，并且上述算法也并不完美，比如对于第一种，如果数据是关于坐标轴完全对称，总和为0，无法进行除法运算，应该如何处理？ 类似，对于极大值标准化，图5-2 中所示变量3 的极大值为0，同样无法进行除法运算，均会造成处理上的不便。

此外，灰色关联度无法处理负相关，如图5-3 所示。

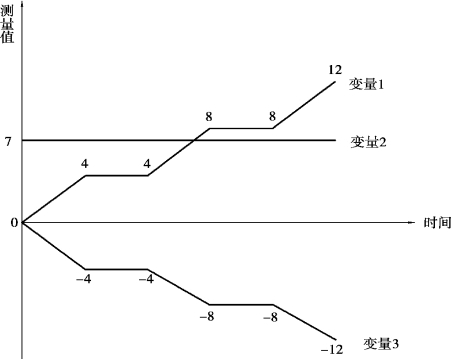
图5-3　用于解释灰色关联度的变量变化曲线

在图5-3 中，3 条曲线分别代表了3 个变量随时间变化的结果，每个变量均有6 个测量值，对于变量1，很明显变量3 与其有着很明显的关联性，即完全按照变量1 的负方向变化，而变量2 和变量1 无任何关系。并且，变量1 和变量3 不存在倍数关系，处于同一量纲，不存在量纲不同影响计算结果的情况。

下面分别根据3 个变量的测量值，计算变量1 和变量2、3 之间的灰色关联度，将变量1 视为y，分别将变量2、3 视为x1 和x2。

首先计算图5-1 所示的公式（5-2）A 部分，如下所示：

之后计算图5-1 所示的公式（5-2）B 部分，如下所示：

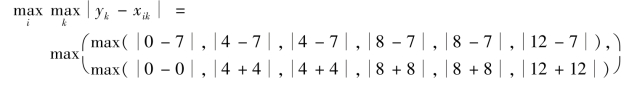
计算变量1 和变量2 之间的灰色关联度，如下所示：

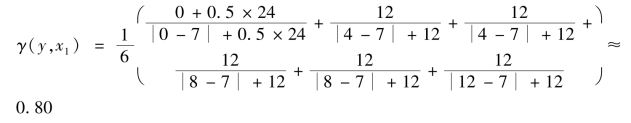
计算变量1 和变量3 之间的灰色关联度，如下所示：

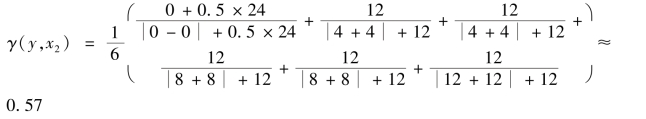
计算结果显示，变量1 和变量2 之间的灰色关联度要明显高于变量1 和变量3，显然和客观事实不符。原因也很简单，即变量1 和3 的变化趋势是完全相反的，所以画出来的曲线在几何上的距离相距非常远，灰色关联度不认为这两个变量具有相关性。因此，本著作推荐采用经典的相关系数计算相关性。

对于两变量x，y，其之间的相关系数计算公式如下：

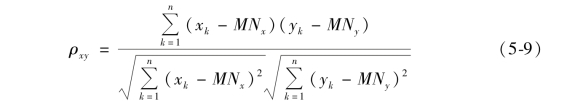
其中，MNx 表示平均值，计算方法见式（5-6）。

相关系数不会受到量纲的影响，并且相关系数能够表示负相关性，相关系数从1 变化至0 再至-1，表示两个变量从正相关至不相关再至负相关。