从实验角度出发，实现热误差黑箱化

对于工程应用，机床零部件的热变形研究虽然复杂，但复杂背后也是遵循物理规律的。因此，从机床受热产生温度变化，到引起热变形传递至工作台和刀具，无论过程多么复杂，其间是必然存在某种特定的联系的。机床结构设计越稳定，其联系规律性越强，黑箱化建立的规律数学模型越稳健。这是黑箱化的技术基础。

基于此，为机床热误差的研究提供了一种新思路，对于结构性能稳定的机床，采用黑箱化的方法，参考定性的机床内部结构热特性，实验仅测量刀具和工作台之间的热位移，是容易实现的。然后从测量数据中找出机床热误差和温度之间的联系规律，利用此方法探究热误差的变化特性会简单得多。

如图3-4—图3-8 所示，是对一台Leaderway V-450 型立式加工中心进行直接热误差测量得到的结果，共有5 次试验，分别记为K1 ～K5。

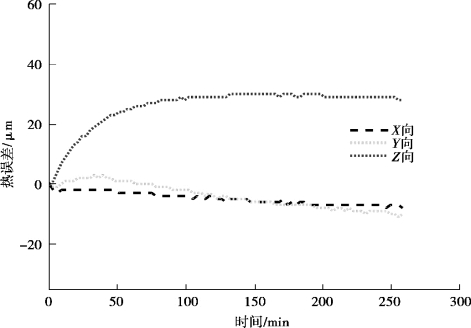
图3-4　热误差测量结果-K1

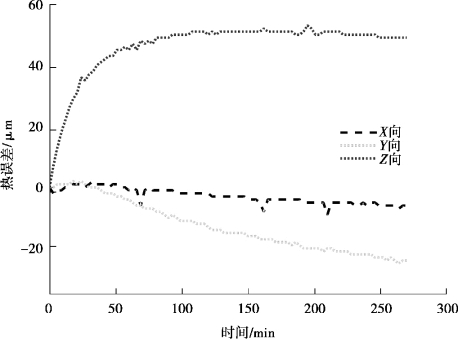
图3-5　热误差测量结果-K2

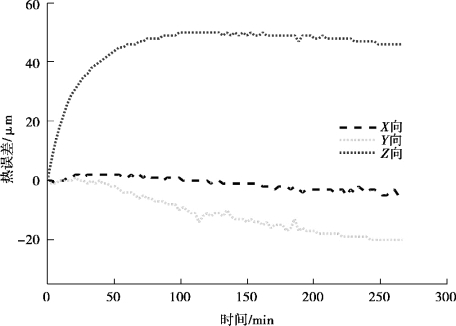
图3-6　热误差测量结果-K3

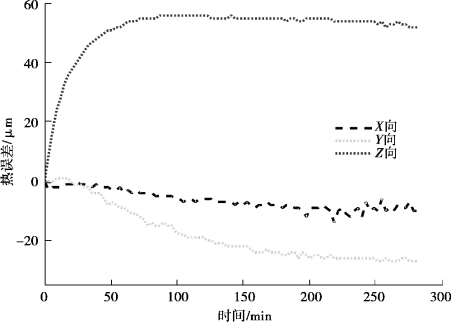
图3-7　热误差测量结果-K4

图3-4—图3-8 中，一共对X，Y，Z 3 个方向的热误差进行了测量，不难看出，五次测量结果热误差的变化趋势十分接近，热误差幅值开始变化快，随着时间的变化越来越慢，到最后基本维持恒定。Z 向热误差变化最大，变化方向朝向正方向，Y 向其次，但朝着负方向变化，X 向变化不明显。说明机床热误差变化稳定，是存在规律的。

在测量热误差的同时，也在机床的主要热源附近大范围安置了20 个温度传感器进行温度测量，测量结果如图3-9—图3-13 所示。

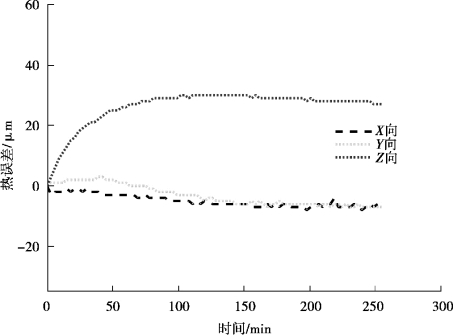
图3-8　热误差测量结果-K5

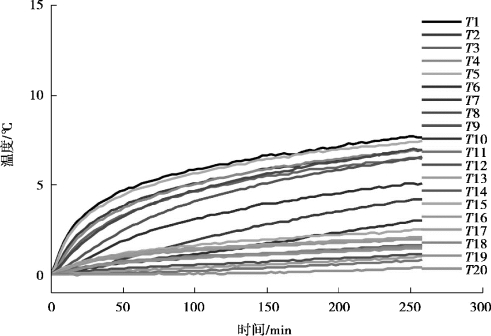
图3-9　温度测量结果-K1

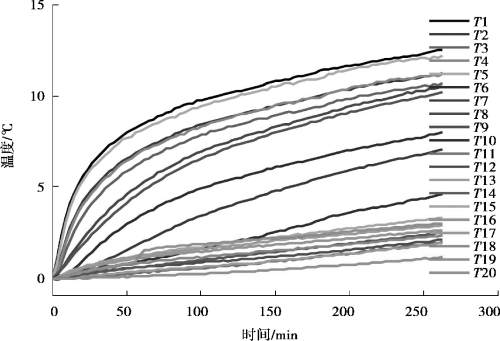
图3-9—图3-13 分别显示了K1 ～K5 批次实验在测量热误差时，对应温度的测量结果，20 个温度传感器分别记为T1 ～T20。根据图3-9 和图3-13 也可以看出，机床温度变化的趋势十分接近，与热误差变化对应，也是一个由快到慢再到维持恒定的变化过程，这是因为随着机床温度的上升，机床和周围环境温度之间的温差逐渐增大，加快了热量发散的速度，最后当热量发散的速度和热源产热的速度达到平衡时，机床温度不再继续变化。

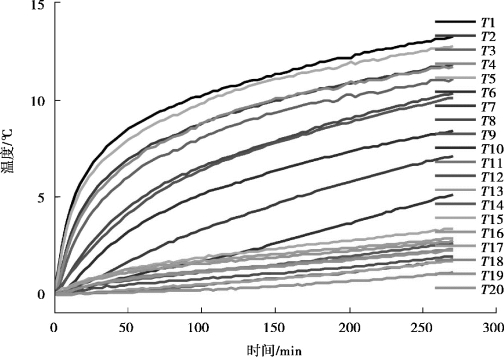
图3-10　温度测量结果-K2

(www.xing528.com)

图3-11　温度测量结果-K3

比对图3-4—图3-8 和图3-9—图3-13 可以明显发现，热误差的变化和温度变化的节奏是一致的，并且5 批次实验数据均显示相同的趋势。K2 ～K4批次实验温度变化较大，对应热误差也变化较大，K1，K5 批次实验温度变化较小，对应热误差的变化也较小，说明测量数据中必然隐含着某些联系。黑箱化方法是具有可行性的。

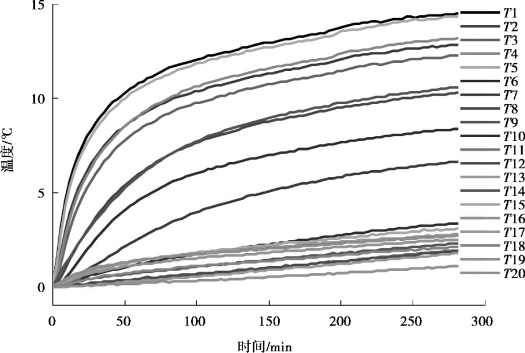
图3-12　温度测量结果-K4

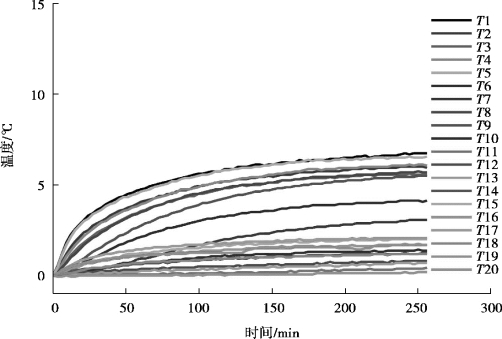
图3-13　温度测量结果-K5

同时，根据图3-9 和图3-13 可以看出，20 个温度测点得到的温度变化趋势也十分接近，这是热传导的作用所致，使得各温度测点之间产生了耦合联系，这为机床热误差黑箱化的研究提供了另一种便利：可以利用个别温度点来替代整个温度场的变化信息。进而机床黑箱化的模型可简化如下：

如图3-14 所示，对于机床内部结构，黑箱化模型将其视为联系温度和热误差之间的纽带，利用一个公式进行替代。几个特定的温度测点是模型的输入变量，热误差是输出变量。

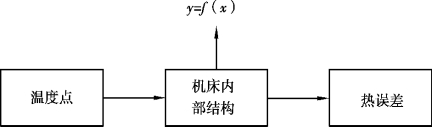
图3-14　机床热误差黑箱化模型

对于研究人员来说，黑箱化模型中值得关注的研究点有两个：第一是如何确定模型中的输入变量，即温度测点的位置；第二是如何确定联系温度和热误差之间的模型公式。通常，将确定的温度测点位置称为温度敏感点，将模型公式称为热误差模型。两个研究点的研究对象均为热误差测量数据，而使用的工具是以统计理论为基础的数学分析算法。因此，对于黑箱化模型，其实研究点更偏向采用数学统计算法，用于从数据中挖掘出的温度敏感点和建立的热误差模型具有较高的准确性。

目前，对于温度敏感点的确定和热误差模型的建立涉及的数学算法，J.G.Yang 提出了根据各温度测点之间的关联性对温度测点进行分组筛选，以减小选出的温度敏感点之间共线性的思想，并采用多元回归算法建立热误差模型。J.G.Yang 提出根据各温度测点和热误差之间的综合灰色关联度的大小对温度测点进行分级，从各级中选出一个与热误差之间综合灰色关联度最大的温度测点作为温度敏感点，最后采用多元回归算法建模。H.T.Wang 利用模糊聚类算法对温度测点分类选择温度敏感点，并利用神经网络算法建模。E.M.Miao 提出结合模糊聚类结合灰色关联度算法对温度敏感点选择，并利用多元回归算法建模的热误差稳健性建模方法。J.Yang 利用模糊聚类选择温度敏感点，采用神经网络算法建模。T.Bo 利用对温度测点进行分组选择温度敏感点，采用多元回归算法建模。Ali M.Abdulshahed 利用模糊聚类结合灰色关联度算法选温度敏感点，采用神经网络算法建模。T.Zhang 利用模糊聚类和相关系数选择温度敏感点，采用内积多元回归算法建模。J.S.Chen 和杨庆东同时采用多元回归和神经网络算法对热误差进行建模，通过比对发现两种建模算法精度差异很小。H.Wu 对机床结构进行分解，将主要热变形结构附近热源作为温度敏感点，利用神经网络算法建模。Y.Zhang 利用灰色理论对神经网络模型进行优化，改善了模型的收敛性和精度。Q.J.Guo将相关性大于一定值的温度测点分为一类，再从每组中选择和热误差相关性最大的温度测点作为温度敏感点，并结合神经网络算法进行建模。C.W.Wu利用多元回归算法对高转速下的数控机床热误差进行了建模。C.H.Lo 根据温度测点之间的相关性进行聚类，之后根据聚类结果，以模型精度最优作为目标，采用遍历优化的方式选择温度敏感点，并结合多元回归算法建模。R.Ramesh 采用支持向量机算法进行建模。R.J.Liang 将和热误差相关性较强的温度测点作为温度敏感点，并结合神经网络算法建模。谭峰和J.Han 利用模糊C-均值法对温度测点聚类进行温度敏感点选择，并结合神经网络算法建模。J.H.Lee 利用多元回归算法对热误差进行建模。马廷洪和马驰分别通过粒子群算法和遗传算法对神经网络进行优化后建立热误差模型。葛济宾、王时龙和Q.Liu 利用模糊聚类结合灰色关联度算法进行温度敏感点选择，并利用多元回归算法进行建模。吴昊利用神经网络算法建立热误差模型。林伟青采用支持向量机算法进行建模，并通过最小二乘算法对其中的关键参数进行了自适应优化。项伟宏采用逐步回归算法对温度敏感点进行选择，并结合多元线性回归算法进行建模。李永祥将时间序列算法和多元回归算法相结合进行热误差建模。郭前建利用蚁群算法对神经网络进行优化建立热误差模型。闫嘉钰根据机床结构对温度测点进行分类，并根据灰色关联度从每一类中选择和热误差关联性最大的测点作为温度敏感点。凡志磊利用偏相关分析算法进行温度敏感点选择，以保证选出的温度敏感点之间具有较低的共线性，进而结合多元线性回归算法建立热误差模型。李泳耀将神经网络算法和多元回归算法进行结合，利用多元回归建立线性热误差模型后，再将模型预测结果带入神经网络进行非线性部分的修正，以提升模型精度。李逢春将欧氏距离和相关系数的距离综合作为温度测点聚类的依据，将相关性强的温度测点聚为一类，再从每一类中选择和热误差关联性最强的作为温度敏感点，并利用多元回归算法建模。蔡力钢利用粗糙集理论结合偏相关分析算法对温度敏感点进行聚类选择，并结合多元回归算法建模。马跃利用模C-均值法对温度测点聚类，并结合灰色关联度算法从每一类中选择和热误差关联性最强的作为温度敏感点，并结合多元回归算法建模。邬再新利用模糊聚类结合灰色关联度算法进行温度敏感点选择，并利用神经网络算法进行建模。王桂龙利用模糊聚类结合灰色关联度算法对温度敏感点进行优化选择。魏效玲、谢杰、马廷洪采用神经网络算法建立热误差模型。孙志超、穆塔里夫·阿赫迈德，李书和与仇健采用多元回归算法建立热误差模型。

根据上述研究可以看出，温度敏感点选择方法的常用基本步骤为：先对温度测点进行分类；然后从各类中选择和热误差关联性较大的温度测点作为温度敏感点。常用的建模算法根据应用方式，可分为离线建模算法和在线学习建模算法。离线建模算法特点为当有新的建模数据需要融入模型时，必须将原有的数据找回，并附加新的数据重新建模，即不具有学习功能，典型的代表为多元回归算法。在线学习建模算法具有学习功能，能够随时根据新的建模数据在线更新模型，典型的代表为神经网络等。

相对于白箱化的研究方法，黑箱化虽然简单，但也存在着很大的问题，即缺乏对机床热误差的深入了解，不知道其中的变数如何。图3-15、图3-16 分别显示了机床在两种运行模式下的温度场分布状况，图3-15 显示的是机床在未进行实际切削的空转状态，图3-16 显示的是进行实际切削的实切状态，其他的运行条件一致。

图3-15　空转状态下机床温度场分布图

图3-16　实切状态下机床温度场分布图

从图3-15 和图3-16 可以看出，在空转和实切两种状态且相同转速等运行参数条件下，机床的温度场在温度数值上差异不大，但温度场分布规律发生了明显的变化。机床运行状态的变化会影响机床的热误差特性，本著作后续章节也会对此做进一步研究，结果表明空转和实切状态下的热误差特性差异性较大，建立的模型相互之间预测误差也较大。

这说明黑箱化建立的预测模型，仍存在较多待解决的问题。当某些条件发生变化，有可能会引起热误差特性的改变，此时建立的预测模型的有效性难以确定，模型的稳健性不能获得保证。如何采用黑箱化的统计算法解决问题，本著作后面将给予详细说明。