从零件热变形角度出发的热误差白箱化

机床热误差由各零部件的热变形叠加而成，从白箱角度进行研究，目的是掌握各零部件的热变形规律特性，然后计算出机床热误差。有限元为计算零部件热变形提供了有力的数学工具，是研究热变形的主要手段。

机床零部件的热变形源于机床在运行过程中的温度变化。机床热源分布复杂，比如在电机转动过程中，电能一部分转化为动能，一部分被线圈的电阻消耗，以热量的形式散发出来，形成以电机为中心，逐渐向外扩散的温度场；导轨和丝杠等传动部件之间的相对运动，以及切削时刀具和工件之间的高速相对运动，也会因摩擦产生热量并扩散出去。此外，机床的冷却系统、机床的使用环境温度变化等也会直接作用于机床。

在多种热源的综合作用下，机床所处的温度环境呈现时变性和非均匀性的复杂特性。图3-1 所示为机床在加工时，通过红外热像仪拍摄的温度场图片。

从图3-1 可以看出，主轴处温度最高为15.8 ℃，最低为8.3 ℃，相差7.5 ℃，并且可以明显看出，温度并非均匀变化，接近主轴中心部位存在多处高温点，同时温度变化的幅度较大，而远离主轴的部位温度变化较小，这导致机床零部件的热变形不只是几何尺寸上的热膨胀，而是呈现弯曲、扭转等形状上的额外变化。比如对于横梁，通过有限元模拟热源接近上表面和下表面两种情况时，横梁的热变形情况分别如图3-2 和图3-3 所示。

图3-1　机床加工时主轴部位温度场

(www.xing528.com)

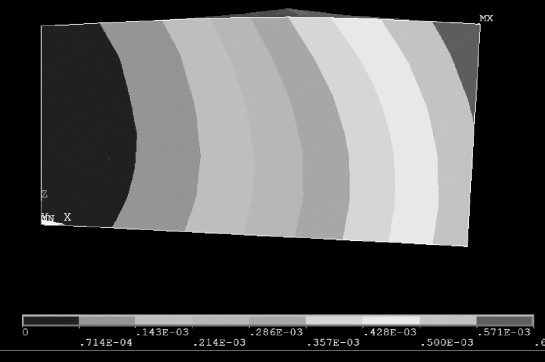
图3-2　横梁热变形模型——热源接近上表面

如图3-2 和图3-3 所示，热源处于不同位置时，横梁的弯曲方向甚至会随之改变，从定性的角度很好解释，如果热源接近上表面，则上表面受热较多，热变形也大于下表面，导致上横梁向上拱起，同理，如果热源接近下表面，则横梁向下凹陷。但如果要定量获取变形量，则最终结果对温度场测量的精确程度极为依赖。

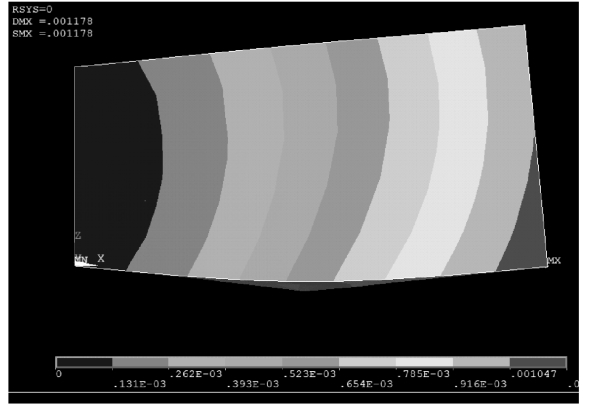
图3-3　横梁热变形模型——热源接近下表面

目前，热误差白箱化的研究进展主要集中于一些零部件的热变形仿真，W.S.Yun分析了机床丝杠和导轨热变形对加工误差的影响，认为丝杠热变形主要引起线性定位误差，而导轨热变形会同时造成倾角误差、线性定位误差和直线度误差；H.K.Kim 建立了机床丝杠的热变形有限元模型，以预测并补偿丝杠引起的热误差； X.Min 考虑了机床轴承温度对机床热传导的影响，将有限元模型的精度进行了提升； H.T.Zhao 建立了机床主轴的热变形有限元模型，以预测并补偿丝杠引起的热误差；E.Creighton 发现热误差对尺寸较小的微型铣床影响尤其严重，于是建立了铣床主轴的有限元模型对热误差进行补偿；蔄靖宇建立了车削中心主轴箱瞬态温度场和热变形仿真模型，分析了其对车削刀具位置变换的影响关系；周顺生在将结构进行简化后，建立了数控铣床有限元模型，分析了机床各部位温度对热变形影响权重，并对影响最严重的区域分布状况进行了归纳；R.Zhu 对主轴热变形引起的轴向伸长和弯曲变形进行了仿真分析；J.Han 提出了一种主轴有限元热变形仿真所需的温度边界条件以及结构等效热传导系数的综合计算方法；C.H.Wu 对机床丝杠的热变形进行了有限元仿真分析。

上述研究虽然定性地解释了机床部分零部件的热变形特性，但对热误差的精确计算帮助较小。首先，机床零部件热变形依赖于温度场、零部件的几何形状和材料属性等多种特性，要确定这些量十分困难。比如温度场的确定，上述研究主要根据机床热源的发热量和热传导建立模型计算温度场，因组成构件复杂，影响热传导因素较多，难以保证计算结果的准确性。如图3-1所示，温度场呈非均匀性，如果利用单点的温度传感器进行测量，虽然理论上传感器的数量足够多，是能够还原温度场的。但实际上，机床内部有很多复杂的机械传动设备和电气设备，关键部件会加盖防护罩，因此，根据有限的温度传感器并不能准确地获得温度场的分布状况。如果采用红外热像仪等大范围温度场拍摄测量设备，由于零部件的遮挡，只能拍摄到最外层零部件的表面温度，获取信息不完整，也无法用于温度场的还原。其次，完整获取所有零部件的温度场，也会受限于目前的计算机的计算速度。因为有限元是一种化整为零的计算方法，需要通过网格将零部件划分为小单元，每个单元自身对应一组求解方程，计算热变形时需要将所有单元的方程联立进行求解，才能求解一个零件的热变形，计算耗时，对整个机体所有零件进行仿真计算热变形的计算速度远远跟不上热变形的变化速度。

从白箱化的角度出发来研究热误差，其优势在于深入机床内部，从本源出发探究机床热误差的产生机理，有利于机床的设计，提高机床的功能性结构优化。