压配结构的设计及力学计算方法——以塑料轮毂和实心钢轴为例

压配结构，又称压入配合、压紧配合，它是两个零件在持久应力作用下，接合部分材料发生弹性变形而互相压紧来实现紧固连接的一种不可拆式连接方法，常见于圆柱形轴和轮毂的组装，如齿轮、滚轮、轴承等环形制品与贯穿于其间轴的连接等。

这种方法实际上采用了金属零件的过盈配合原理，由于用在塑料制品上，所以其力学行为有不同的特点。

1.压配结构制品的受力状况

以轮毂与轴压配结构为例分析如下：

1）轮毂将承受周向拉应力，轴承受周向拉应力和径向压应力，且在过盈量作用下沿装配面垂直方向产生接触压力和切向应力。另外，在接触压力作用下装配面间还产生了摩擦阻力。不难判断，在压配连接中，具有两种可能的失效形式：如果作用在轴上的压应力超过轴材料的屈服极限，轴将破裂；如果作用在毂上的切向应力或拉伸应力超过毂材料的拉伸极限，则毂将被胀裂。由于无论是塑料毂与塑料轴压接，还是塑料毂与金属轴压接，轴损坏的可能性都比较小，因此多数情况下，主要考虑作用于毂内表面上的拉伸应力。为使组装配合安全可靠，这里的拉伸应力应低于材料的拉伸屈服强度。

但是压配过程产生的这些力具有阻止制品轴向移动和承担传递力矩的功能，它们决定了装配力或拔出力的大小。

2）轮毂和轴在开始装配时产生的接触应力较大，对制品的作用力大，压配可靠性也高，但随着工作时间的延长或温度的升高，因发生应力松弛，从而会导致接触压力和装配可靠性下降，甚至结构失效。因此，需进行抗蠕变性和安全性设计。

3）结构可靠性与诸多因素的关系。由前面的叙述可知，在压配结构设计中材料的性能、过盈量、轴与毂的几何尺寸等参数对接触压力、装配力、传递力矩、压配制品承载能力有关键的影响。此外，还有诸多因素，如压配件的尺寸精度、表面粗糙度或表面各类滚轮花槽、压配制品孔及轴有无锥度（制品都不应有脱模斜度等锥度），空心轴或开设弹性装夹槽的轴等结构也都会直接影响压配结构效果。

综上所述，不同条件下的压配结构有不同的设计及力学计算方法。这里仅以塑料轮毂和实心钢轴为例介绍压配结构的计算。

2.压配结构的力学计算

（1）通用计算法

1）干涉量I，即过盈量为

I=轴外径D_s-毂孔内径D_i

它是决定压配时力学状态的基本参数，当按制品设计确定D_s或D_i中的一个尺寸后，则另一尺寸由I值来决定。

I值可用各种塑料的I-轴径/毂外径比曲线来求得，但曲线是在特定条件下测试的，有局限性，故推荐用计算法求I值。

实心轴的压力装配的直径干涉量I，有三种计算式。任何轮壳材料与轴材料组合的压力装配的干涉量为

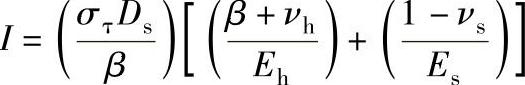
其中，轮壳孔座筒体的几何因子为

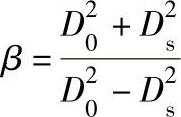
倘若轮壳与轴是同一塑料的压力装配，其干涉量可用

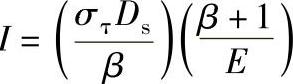
轴用钢制造，E_s≫E_h。塑料轮壳与金属轴的压力装配干涉量为

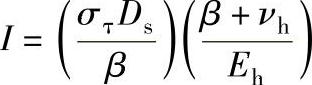
配合柱面上径向接触压力是

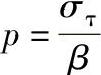
各式中，轮壳孔座上周向应力为σ_τ；D₀是毂外径；D_s是轴外径（装配名义直径）；E_h为毂料拉伸弹性模量，E_s为轴料弹性模量；ν_h为轮料泊松比；ν_s为轴料泊松比。

2）压力装配可传递力矩，也可称为扭转强度或滑动力矩为

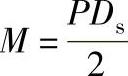
3）轴向的轴与孔的压入装配力为

P=μF=μpA=μpπD_sL式中，μ是轴与孔表面摩擦因数；F是轴与孔间表面接触压力；A是轴与孔配合柱面的表面积；L是轴与孔间轴向配合长度。

（2）实心轴和厚壁轮壳压配结构计算

1）室温下的过盈量计算：

①作用在配合柱面上的接触压力为

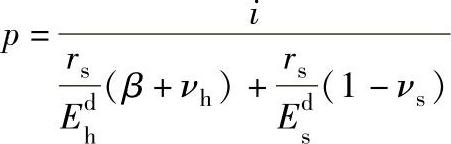
②装配时需压入力为

F_in=2πfLr_sp=F_out(www.xing528.com)

③连接件可传递的转矩为

M=F_inr_s=2πfLr²_sp

④轴与孔座接触柱面间的径向应力为

σ_r=p

⑤轴与孔座接触面间的周向应力，也称切向应力为

στ=βp

⑥周向应力στ使厚壁筒体周向伸张，它必须小于材料的拉伸屈服应力，即

στ≤σ_y，h

⑦允许的最大直径过盈量为

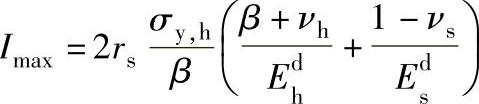
2）高温时过盈量计算：

①高于室温T的总过盈量为

I^T=2（r_s^T-r_i^T）

②温度升高ΔT，轴半径的增量为

Δr_s^T=r_s（1+α_sΔT）

③孔座在温度升高ΔT，孔的半径增大量为

Δr_h^T=r_s（1+α_hΔT）

④在室温下的总过盈量为

I=2（r_s-r_i）

⑤由上可得温度T时直径过盈量为

I^T=I-2r_s（α_h-α_s）ΔT

金属光轴与塑料孔座的过盈配合，由于金属材料的热膨胀系数小于塑料，使用时温度升高会使过盈量减小，失去传递转矩的能力。如果塑料实心轴的膨胀系数α_s等于或大于塑料孔座α_h，可保持或增大总过盈量。

3）安全系数计算。孔座材料的屈服应力是压力装配的极限。首先要防止孔座在装配和使用中破裂。对于纯聚合物，取材料特征安全系数n₁=1.5；对于各种增强塑料n₁=3。还需考虑塑料件成型过程中的强度损失。如带轮注塑件，由于浇口的单向偏置而有熔合缝存在。熔合缝区的力学性能低于无缝材料，必须考虑工艺特征系数n₂=1.7～2.3。对脆性的无定形聚合物应取大值；结晶型聚合物应取小值。如PET热塑性塑料的熔合缝系数大于0.8，考虑生产工艺波动的影响，取n₂=1.7～2。因此，被连接塑料件的设计应力为

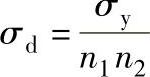
（3）计算中的几点说明 主要包括如下几点：

1）关于轴槽定位结构。图19-96所示为一种采用轴槽定位的压力装配设计。内径D_i的轮壳孔座首先要通过轴的外端轴颈D_s1，才进入装配固定的轴槽位置。此割槽段的轴径D_s2。它们有D_i<D_s2<D_s1关系，且装配槽上直径干涉量I=D_s2-D_i。此种压力装配时，考虑轴颈D_s1是短时的过盈配合，干涉量可较大。轮壳孔座上周向应力στ可取轮壳材料拉伸屈服应力σ_y的40%～60%。而轴槽D_s2是长期的过盈配合。为了减少应力松弛和避免轮壳开裂，干涉量应较小。轮壳上应力στ为材料屈服应力σ_y的20%～25%。此种压力装配设计，可提高在环境温度和湿度变化下的工作寿命，也提供了轮壳在轴上的轴向定位。

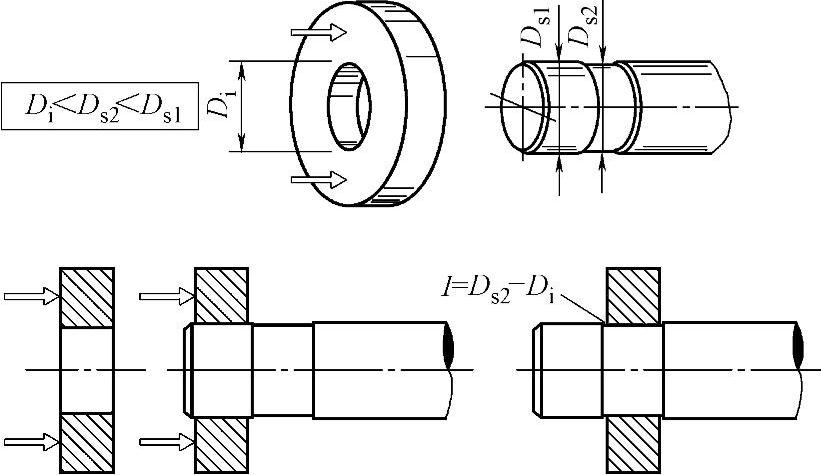
图19-96 轴槽定位的压力装配

压力装配连接的技术难题是轴与孔的配合精度要求高，连接强度随着使用时间增长而下降。但仍有一些改进的设计方法可实施，如图19-97所示，具有直槽的塑料轴能提高抗扭力矩。塑料件随着时间蠕变时，材料可流入沟槽，连接强度减弱趋势会减缓。还有横向槽、网格状槽以及波纹状的轴表面，来提高连接强度。需提出的是，在塑料件与金属件的压配连接中，在刚性的金属件上制成防松倒钩、棘齿一类的结构，可有效提高连接牢度。

2）关于选择设计值。在I的计算公式中，毂孔周向应力σ_τ参数是一个设计设定值，它是根据材料的拉伸屈服强度，是按制品所处的环境温度、湿度、化学环境及制品使用时间长短酌情确定的，其值应比材料最大允许值小，要考虑充分的安全系数才能保证压配结构的可靠性。

在压配连接设计中，材料通常是给定的，在已知材料的性能参数和连接件几何参数的情况下，往往可以根据允许的设计应力值计算出连接件所需的装配力和扭转力矩，并计算出合理的过盈量，从而确定可行的轴与毂的公差值，以便确定零件的设计方案。

如上所述，材料的性能参数、连接件的几何参数和载荷（装配力、力矩）是装配设计中的三个重要变量，其中任意两个变量如果已知，第三个变量就可以被确定，有关的计算公式可以从相应的设计手册中找到，此处不再赘述。

3）关于材料的选择。轴毂压配连接中，轴毂可以是同一种或不同种的塑料材料，也可以是金属与塑料件的连接。脆性材料、对应力比较敏感的材料一般不宜用作连接材料，而韧性好的聚合物可使压配连接变得相对容易。温度升高对不同材料之间的压配，会因热膨胀而引起过盈量的变化，因此如果用塑料与金属作压配接合，采用增强或矿物填充的塑料材料就比较合适。此外，长期应力作用下的压配连接要考虑到塑料材料的蠕变性和应力松弛，设计时应注意选择抗蠕变性好的材料，材料的蠕变曲线可以对预期的工作寿命进行评估。

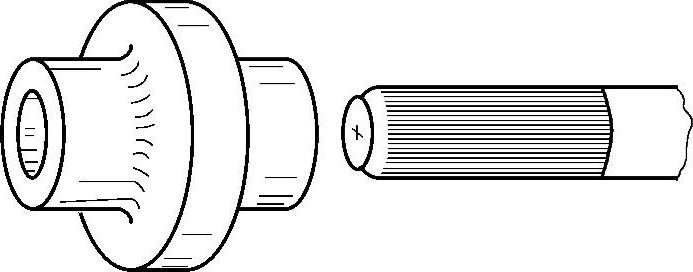
图19-97 直槽轴的压力装配