搭扣连接结构及计算设计

搭配结构，又称搭扣结构或弹性连接结构，是可拆式组合结构，其形式很多，但基本原理都是利用塑料的良好弹性和柔软可塑性，将一个单件设计成弹性可变形件，可与另一组合单件弹性结合成一体，实现可随意装拆的功能，如笔套（帽）与笔杆连接等。搭配结构的形式有悬臂搭扣、环形搭扣、扭转搭扣等。

1.悬臂搭扣结构

悬臂搭扣连接是搭扣连接中最基本、最常见的，也是变化最多的连接形式。一种典型的悬臂搭扣连接如图19-89所示，图中左边的部件为一带有凸缘的悬臂梁，称之为悬臂钩，而右边的接合件以扣槽为结构特征。

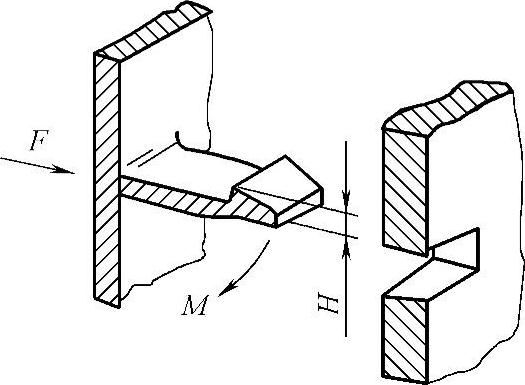
图19-89 悬臂搭扣连接

F—悬臂钩装配时的正向推进力 M—悬壁钩装配时承受的弯曲力 H—凸缘高度

悬臂钩可以看成是由梁和凸缘两个部分组成的，梁和凸缘的设计是悬臂搭扣连接设计的关键。

在图19-89中，悬臂梁为搭扣的基本元件，只要改变悬臂头部及钩槽的尺寸形状、即可设置成许多形式的悬臂搭扣连接结构，如图19-90所示。悬臂搭扣结构形式多样，这里主要讨论悬臂梁的结构参数及弹性计算。

图19-91所示为悬臂钩基本结构参数。

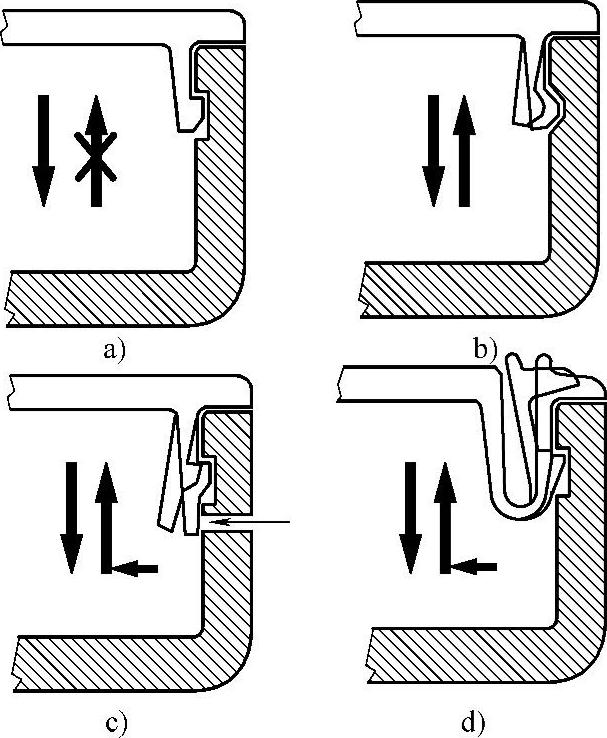
图19-90 常用于塑料制件组装的悬臂搭配梁结构

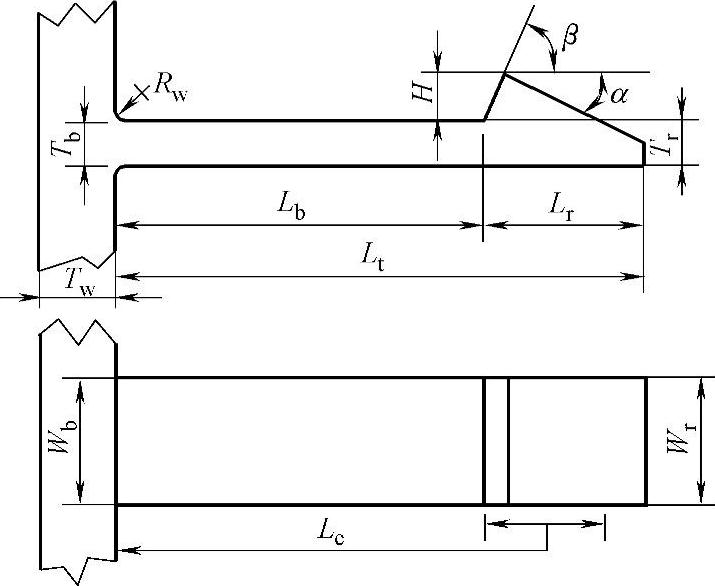
图19-91 悬臂钩的结构形状和尺寸参数

L_t—悬臂钩的总长度 L_e—悬臂钩的有效长度 L_b—梁的长度 L_r—凸缘部分长度 T_w—壁面的厚度 T_b—梁根部厚度 T_r—凸缘有效工作部位厚度 W_b—梁根部宽度 W_r—凸缘部分的宽度 R_w—梁与壁连接处半径 H—凸缘高度 α—咬合角 β—脱开角

1）梁的截面形状有三角形、矩形、梯形、圆形、椭圆形、半圆形和扇形等，矩形截面是最常见的结构。

沿梁的长度方向，如果截面形状和尺寸大小不变，则为等截面的连续梁。如果沿长度方向，梁的厚度逐渐变小或者宽度逐渐变小，抑或宽度和厚度同时逐渐变小，这样的梁就称作是锥形梁。

采用锥形梁可增大悬臂梁的最大变形量，使应力分布更均匀，节省材料。如梁厚度锥化成原厚度的一半，在其他参数不变的情况下最大允许变形量可超过均厚梁的60%。

2）梁根部厚度T_h。T_h越大，梁挠曲性越差，一般取制品壁厚T_w的60%。

3）梁长度L_b。L_b越长，挠性越好，越柔软，但保持力下降。另外，L_b还受制品装配空间和装配件尺寸限制。因此，L_b一般应为（5～10）T_h，对较硬脆的塑料应取大的L_b/T_h比值。

4）梁的宽度W_b。W_b增大可增加梁强度，但装配力增大，同时宽度锥化的效果不及厚度锥化。因此，多数梁宽通长不变，一般W_b<L_b/2。

5）凸缘高度H。H值与梁装拆时的变形量、装拆力大小有关，它应与梁的T_h、L_b、W_b尺寸和塑料允许变形量有关，一般情况下，当L_b≈10T_h时，H=T_h。

6）咬合角α。α大，则装配力大。一般α为25°～35°，最大不超过40°，但也可用装配力计算公式来验算其是否适当。

7）脱开角β。β大，则脱开力大，如果β→90°，则呈自锁不可拆状态（称为单向搭扣）。可拆结构的β值一般取35°左右，也可用脱开力计算公式验算，但为了保证搭扣牢靠，不会轻易脱开，β应大于α。

8）弯曲变形计算，包括H值或悬臂挠曲量、脱开力、咬合力等。各计算公式为：

h=0.67εL²/t（全长均厚的矩形截面梁）；

h=1.09εL²/t（厚度锥化1/2的矩形截面梁）；

σ=bt²Eε/（6L）；

W=σ（μ+tanα）/（1-μtanα）=σK

W₁=σ（μ+tanβ）/（1-μtanβ）=σK₁

各式中，h是梁许可挠度值，等同于凸缘高度H；t是梁厚度；ε是塑料短期允许变形量；σ是悬臂梁推进时产生的弯曲应力，等同于咬合力；b是梁宽度；L是梁长度；E是材料的弹性模量；W及W₁分别是考虑凸缘与钩槽发生摩擦阻力时的咬合力和脱开力；α及β为咬合角与脱开角；μ为摩擦因数，见表19-174，一般取0.1～0.6。

图19-92所示为α、β与K、K₁的关系。

表19-174 一般塑料材料的摩擦因数

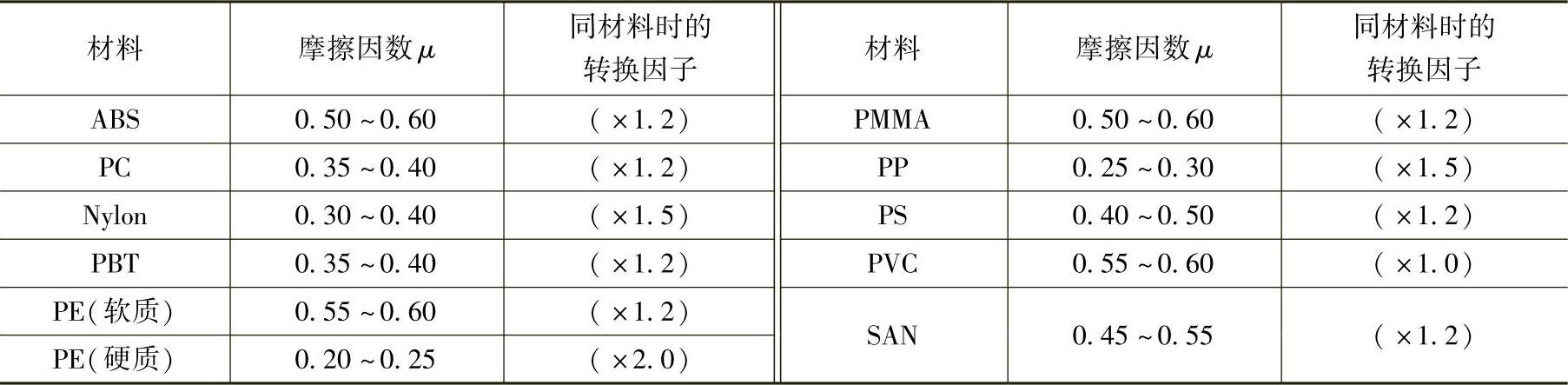
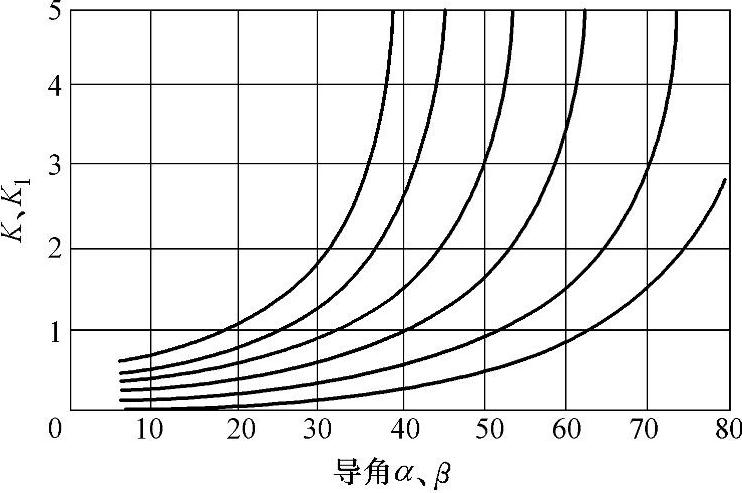
图19-92 导角α、β与K、K₁关系

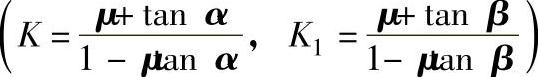
2.环形搭扣结构

环形搭扣结构常用于装配旋转对称的结构件，如轴与毂、瓶口与瓶盖、笔帽与笔杆等制品的装配，其结构举例见表19-175。

环形搭扣的结构形式虽然很多，但基本原理都相似，都是利用一个制品上可径向弹性变形的凸环或凹槽与另一个制品上的凹槽和凸环相咬合实现搭扣组合，且组合后两搭扣制品基本处于无应力状态。一般两搭扣制品中，一件取较硬材料，另一件取较柔软的材料，如果都取较硬的材料搭扣，则装配力和拆卸力较大，且易发生应力集中而导致破裂。因此，若两者用同一种材料，应选用柔韧材料；如果两者用不同材料，则一般毂、盖类零件取较柔韧材料，轴类制品可取较硬材料。此外，装配牢固性及装拆力大小与凸环、凹槽形状及尺寸参数有关。现以图19-93所示的轴、毂搭扣结构为例，介绍结构设计及计算。

表19-175 环形搭扣结构举例

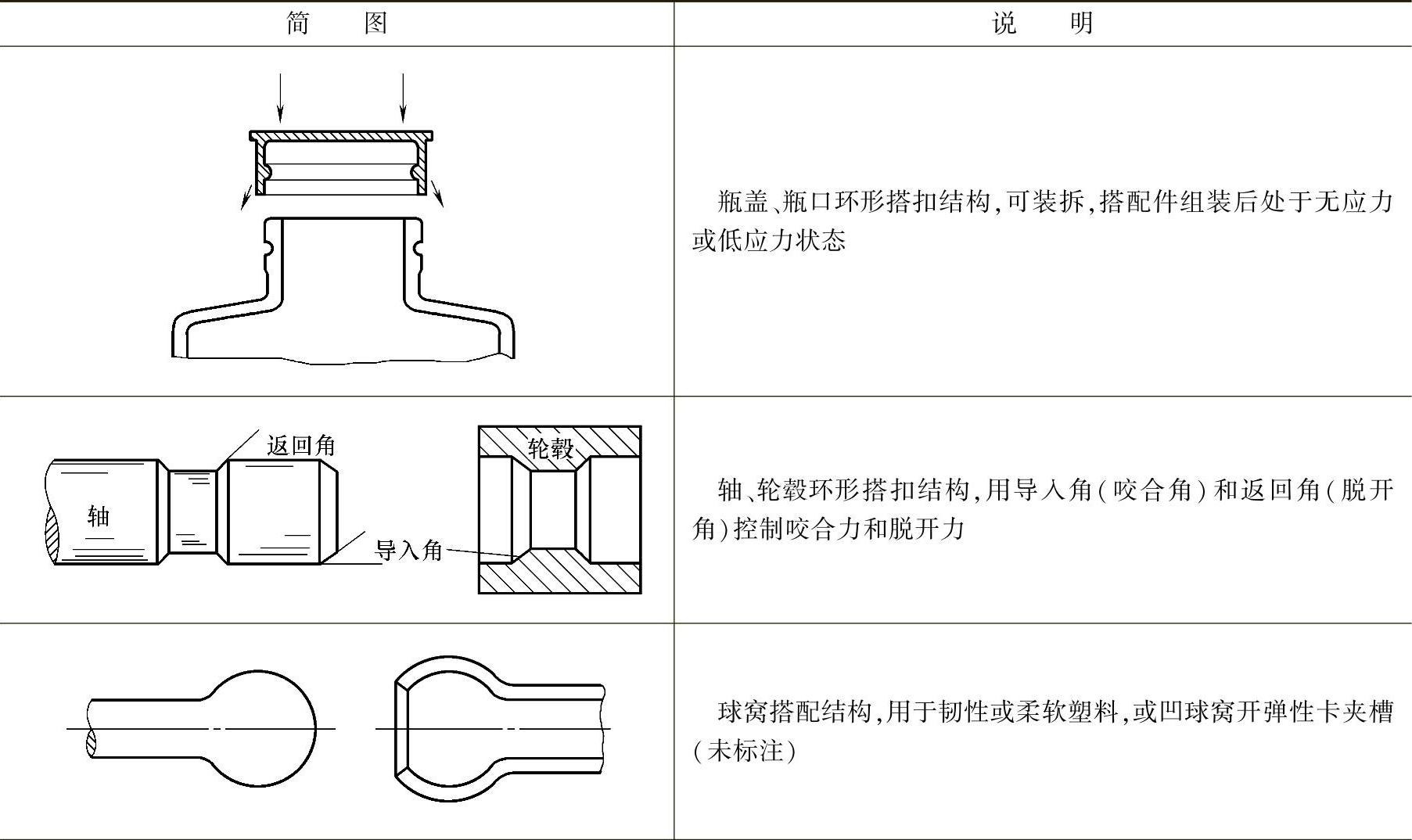
（续）

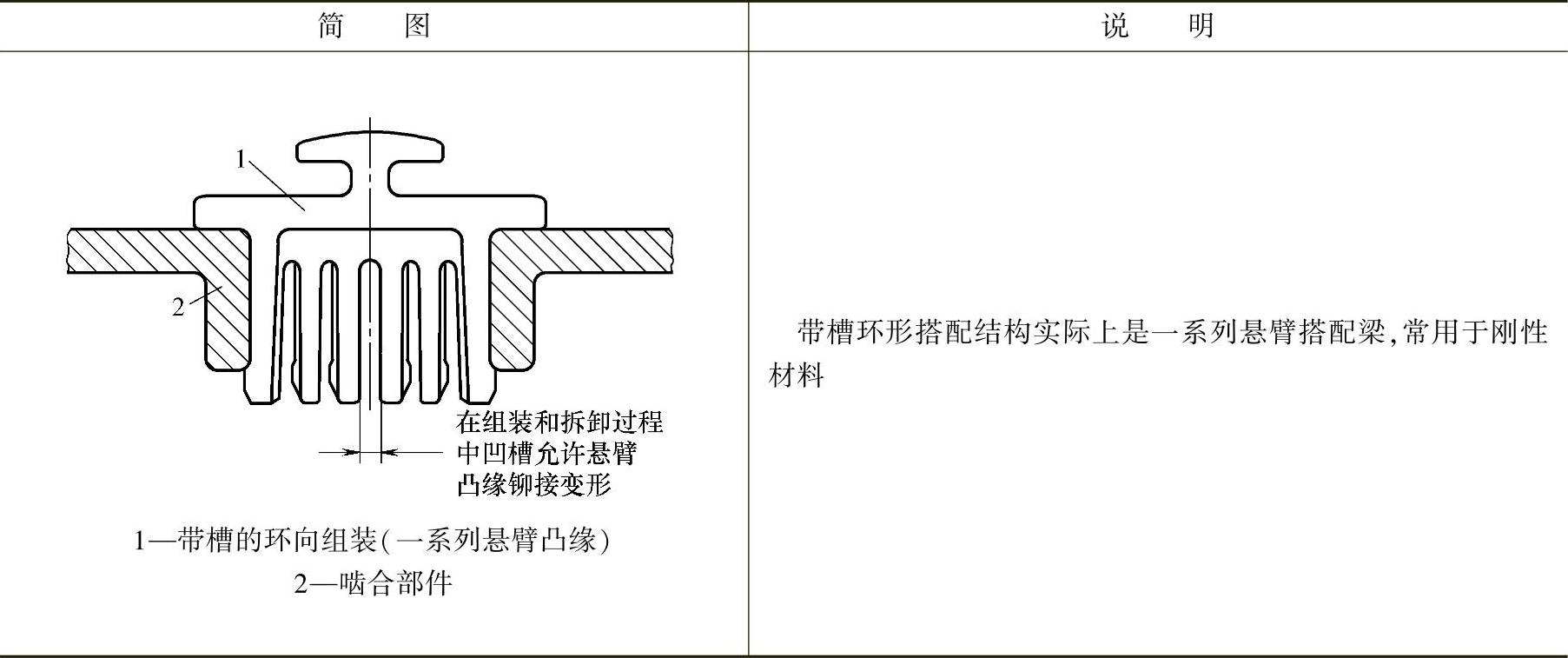
图19-93中，l是指凹槽至端面距离，应合理靠近，否则刚性过大会导致搭扣件破损，可按经验公式计算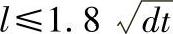：；咬合角α一般为20°～30°；脱开角β为40°～50°。

角度大小与咬合力及拆卸力有关，α≤β时，咬合力即可小于拔出力。如果脱开角为90°，则成为不可拆搭扣。另外，为了满足反复装拆时的强度要求，两件配合不宜过紧，应留有0.5mm（单边）配合间隙。(www.xing528.com)

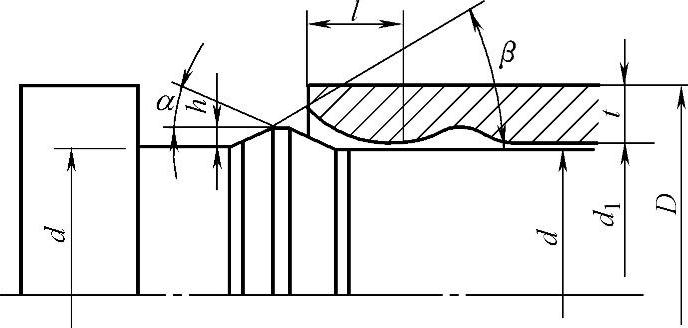
图19-93 轴、毂环形搭扣结构尺寸

1）最大允许凸台尺寸h为

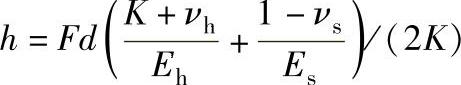
2）毂受径向作用力或毂的膨胀力P为

P=hd²₁EK[ε]

3）几何系数K为

K=（1+ω²）/（1-ω²）；ω=d₁/D

4）导角α插入力F₁为

F₁=P（μ+tanα）/（1-μtanα）

5）导角β拔出力F₂为

F₂=P（μ+tanβ）/（1-μtanβ）

6）毂圆周膨胀量Δd为

Δd=D_平均π[ε]

各式中，F是设计应力值，应在最大应力范围内，但设计应力值随温度、湿度、化学环境及时间变量而变化；E_h、E_s分别是毂材料、轴材料弹性模量；ν_h、ν_s分别是毂、轴材料的泊松比；[ε]是允许拉伸应变；Δd是毂平均直径胀量，等于对应直径方向凸起高度h；μ为摩擦因数。

当α<β时，F₁<F₂，如果轴与毂不在同轴线上，则毂或轴需倾斜一定角度装配，如倾斜角为1°时，F₁会增大1.25倍左右，此时需有足够的引导长度l，以防止歪装，装配直径d越大，则装配力越小。

3.扭转搭扣连接

扭转搭扣连接是由固定支撑轴的杠杆搭钩组成的，如图19-94所示。

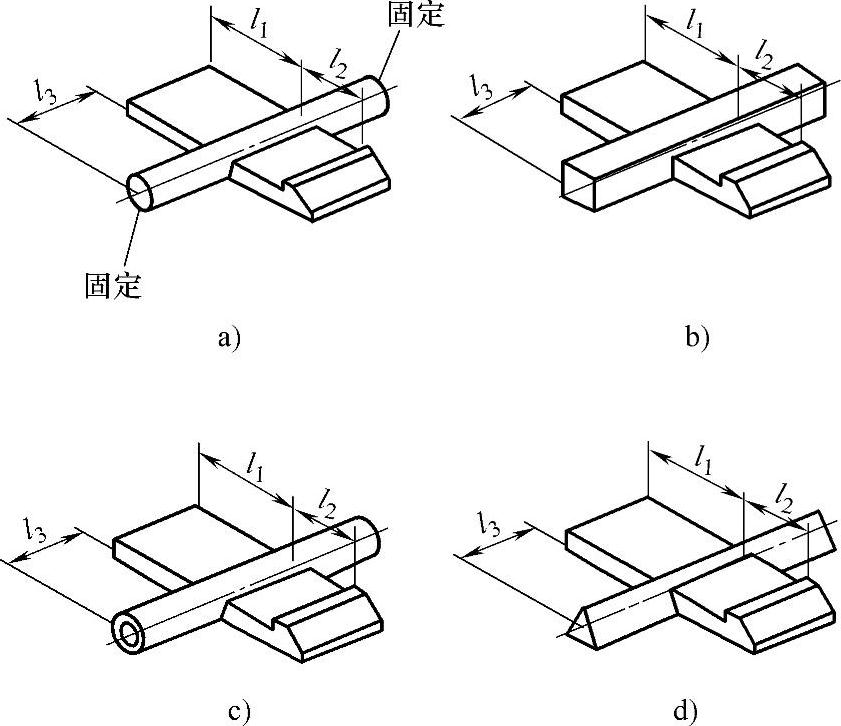
图19-94 扭转杆弹性卡夹

a）圆截面杆 b）正方形截面杆 c）圆环截面杆 d）三角形截面杆

支撑轴常为圆杆，搭扣时向外拉动l₁臂，支撑轴发生扭转变形，搭扣臂l₂向内侧转动与另一塑件上的搭扣咬合固定，开启时只要向内压l₁臂即可脱开搭扣。这种结构常用作箱、盒、容器上合页盖的锁扣。

正方形截面扭转杆的弹性片参量如图19-95所示，各量的计算公式如下：

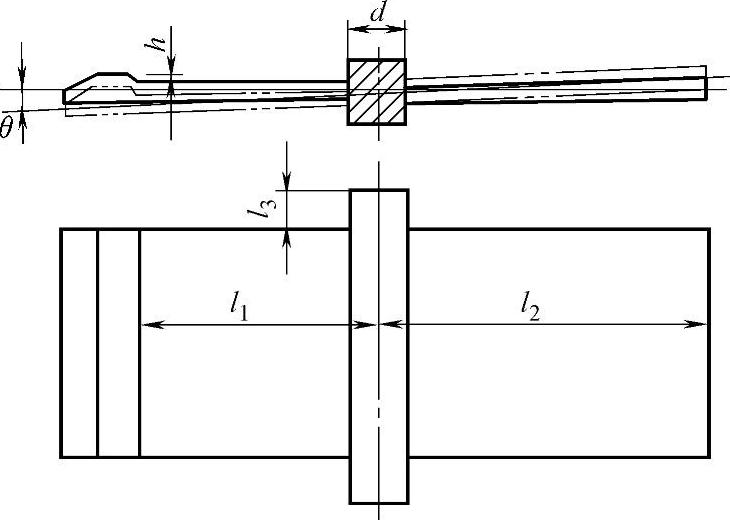
图19-95 正方形截面扭转杆的弹性片参量

1）扭转杆极限及允许扭转应变γ、[γ]为

γ=（1+ν）ε，[γ]=（1+ν）[ε]

2）在γ值扭转角θ为

θ=W_hl₃γ/J_p

3）杠杆片凸起高度h为

h=l₂sinθ

4）向上提l₂时咬合力F_s为

F_s=W_hGγ/l₂

5）向下压l₁时咬合力F_s′为

F_s′=W_hGγ/l₁

6）若推进另一塑件咬合时，在导角α=30°，具有摩擦力时需装配力F_i为

F_i=F_s′tan（α+φ）

7）扭转杆剪切弹性模量G为

G=E/2（1+ν）

各式中，ν是泊松比，一般取0.45；ε、[ε]分别是材料极限和允许拉伸应变；W_h是固定杆扭转截面模量，对圆形杆W_h=0.196D³，极惯性矩J_p=0.098D⁴；对方形杆W_h=0.208d³，J_p=0.141d⁴；D及d分别是圆形固定杆直径和方形固定杆边长；φ是摩擦角。

由图19-95可知，只要利用杠杆原理设计搭扣件的尺寸，便可以以很小的力来开启很紧的搭扣连接，这是扭转搭扣连接的主要特点。为了标明按压的正确位置，通常设计有一个凹部或其他的特征标志。

支撑轴的理想形状是圆柱形，虽然其他截面形状也可采用，但对扭力而言，圆柱形应是最有效的形状，轴的直径和轴的长度也是重要的设计参数。

从应用角度考虑，轴的扭转角度应尽量小，搭扣只要能脱开即可。为了防止使用者将搭扣扭断，可以设置一个阻挡件以防止过度扭转。设计中需要注意的是：①不要将搭扣杆的长度设计得太小，以免扭转角度和扭力变得太大；②开启杆的长度应大于搭扣杆的长度，这样可以减少开启所需的力。