如何进行可靠性设计及指标应用？

可靠性设计也应属于结构设计中的一环节，但因其特殊性本书将其单独列出。

在传统的结构设计中虽然可算出使用寿命或失效期，但都是在将尺寸、载荷、强度等参数设定为某固定值的情况下算出来的。而事实上对一批制品而言，材料性能、加工后的材料性能、尺寸、使用条件都是随机变量，所以即使算出了使用寿命期，但在实际使用过程中一批制品中各个制品的实际使用寿命不尽相同，有先坏后坏之分；如果这一批制品中先坏的数量大，则就意味着使用性能不可靠，反之则为使用性能可靠性高。因此，在20世纪50年代，在机电工程、军工、电子电气工业中推广应用了可靠性设计技术。对一个系统，一个产品，一个零件逐一进行可靠性设计，形成了一门专门科学。如今，可靠性设计已成为优化设计的重要分支，国内机电、电子电气、汽车、航空航天、船舶交通、桥梁工程等行业的专家学者们开展了研究和应用，已将可靠性设计技术用于实践设计工作之中。

事实证明，传统的设计方法只注意性能要求或仅凭经验在设计中采取某些提高可靠性的措施（如采用安全系数），但产品的可靠性仍无法保证，常需试制、试用后才发现不可靠的问题，再改进设计重新试制必然造成人力和物力的浪费，延长产品开发周期，延误上市，降低竞争力。对塑料制品而言，对一些大批量生产的重要制品，尤其在整机中批量应用的制品，如电信、计算机系统中大量应用的塑料接插件，电子电气元件和器件制品等，只有采用可靠性设计才能制造出无故障或少故障运行的制品。

1.可靠性的含意

产品的可靠性是指其在规定的条件下，规定的时间内完成规定功能的能力。规定条件及制品规定功能不同，则可靠性也不同。规定时间增加，可靠性下降。规定功能是指产品明确的具体功能。产品丧失规定功能则称为失效，对可修复产品通常也称为故障。对可修复制品（一般为机械产品）而言，不仅要求在单位时间内出现的故障次数少，出故障间隔时间长，而且要维修时间短，这种要求可称为有效性好（有效性等于工作时间与总时间之比），也就是可修产品维持其功能的能力好。

在可靠性中有些参数的概念不同于传统设计，如产品的负荷或应力等引起制品失效的因素包括力学、温度、湿度、腐蚀等各种因素，另外失效、强度、质量、寿命和成本等参数概念的内涵和外延也均应同样拓展。如时间的概念不仅限于一般的时间概念，也可以是以动作次数，载荷次数、运行距离等参数来表示。

2.可靠性表达方式

产品的可靠性可用可靠性特征量来表示。特征量是用统计方法获得的，可以用函数或图形方式来表达，这里主要介绍函数形式的可靠性特征量（又称可靠性指标值）。在进行新品设计和开发时，设计一开始就应确定指标值作为可靠性设计的依据。对于现有定型产品进行可靠性设计时，设计任务是预测和预防可能发生的全部故障，确定可靠性指标，发现和消除产品中的薄弱环节，找出提高产品可靠性的途径。

可靠性设计可分定量分析和定性分析两种形式。定量分析是确定各种用途的指标值，用概率统计法、布尔代数、马尔可夫过程理论、故障树分析等各种数理统计方法来计算或考虑产品可达到的可靠度或失效概率等可靠性指标。定性分析是通过故障模式影响及危害度分析（FMECA）、事件树分析（ETA）、故障树分析（FTA）、热分析、容差分析等诸多定性分析方法来发现和确定薄弱环节、改进设计、消除隐患，或对事故种类、原因、后果等进行罗列和分析。

可靠性定量指标形式很多，分别用于不同的场合。其常见的几种指标简介如下：

1）可靠度是指产品在规定条件下和规定时间内完成规定功能的概率，符号为R（t），又因它是时间的函数，故也称为可靠度函数。按定义，可靠度的表达式为

R（t）≈（N-n）/N≈[N-n（t）]/N

式中，N是测试制品的总数量；n是在t时间内失效制品的数量。

通常当t≥0时，则R（t）值处于0～1范围内。例如，1000个制品，工作10⁶次后有100个失效，则R（10⁶）=（1000-100）/1000=0.9=90%

2）累积失效概率（又称失效概率）是指制品在规定条件下和规定时间（t）内失效的概率，用F（t）表示。

F（t）=1-R（t）≈n/N≈n（t）/N

F（t）的取值范围为0～1，即意味t增加F（t）也增大。

3）故障密度函数是失效函数F（t）对时间t的微分，用f（t）表示。

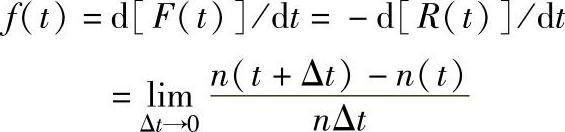
4）失效率，又称故障率，是制品工作到时刻t时尚未失效制品数与经时刻t后的单位时间内的失效制品数之比，用λ（t）表示。失效率是时间t的函数，故又称失效率函数，或故障率函数，或风险函数。按定义其关系式为：

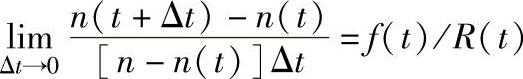
在工程中，失效率可按下式计算：

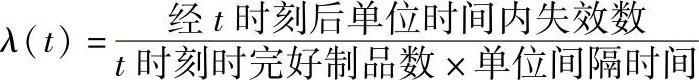
例如，100个制品工作80h尚有50个制品完好，经81h后又失效2个制品，则失效率λ（80）=2/（50×1）=0.04=4%。

5）平均寿命。对不可修复制品，平均寿命是最常用的寿命指标之一，其定义为制品从开始使用起到失效这段有效工作时间的平均值（或平均工作次数），通常用MTTE（或用符号θ）表示。对可修复制品，平均寿命指平均无故障工作时间。

6）可靠寿命是指可靠度为R值的工作。时间t称为可靠寿命，一般用P_r表示，r为可靠水平。P_r应满足R（P_r）=r的关系式，也就是在可靠寿命期内制品可靠度应达到可靠水平。

7）中位寿命指r=0.5时的可靠寿命，一般以P_0.5来表示，R（P_0.5）=0.5。(www.xing528.com)

8）特征寿命指可靠度为R=e^-1时的工作寿命，用P_e-1来表示，R（P_e-1）=e^-1。

9）维修度指可维修制品在发生故障或失效后在规定条件下和规定时间（0，τ）内完成修复的概率，用M（τ）来表示。与其相应的指标还有平均修理时间MTR和修复率μ（τ）。μ（τ）是指维修时间已达到某一时刻，但尚未修复的产品在该时刻后的单位时间内完成修理的概率。

10）有效度，又称可用度，是指可维修产品在规定条件下使用时，在某时刻t时具有或维持其功能的概率，用A来表示，其关系式为：

A=MTBF/（MTBF+MTTR）=μ/（μ+λ）

式中，MTBF、MTTR分别是工作时间和维修时间；μ、λ分别是失效率和修复率。

11）可靠性指标的关系及应用。在上述各项指标中，R（t）、F（t）、f（t）、λ（t）四个基本指标互相有联系关系，只要知道其中的一个，则所有特征量均可求得。如当失效率为常数λ时，则各指标分别为：

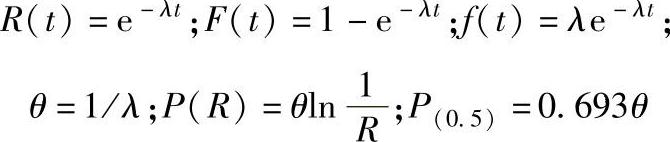
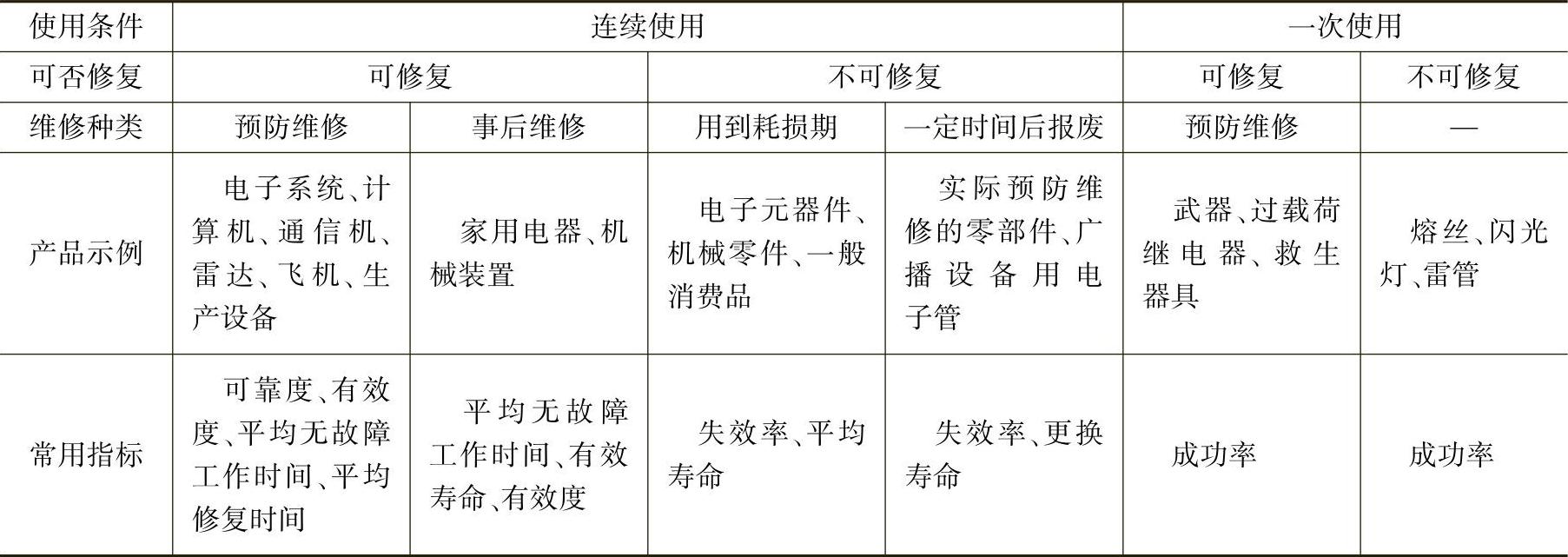
可靠性指标种类很多，在不同使用条件时选用不同的指标。机械零件类产品常用的可靠性指标见表19-2。

表19-2 机械零件类产品常用的可靠性指标

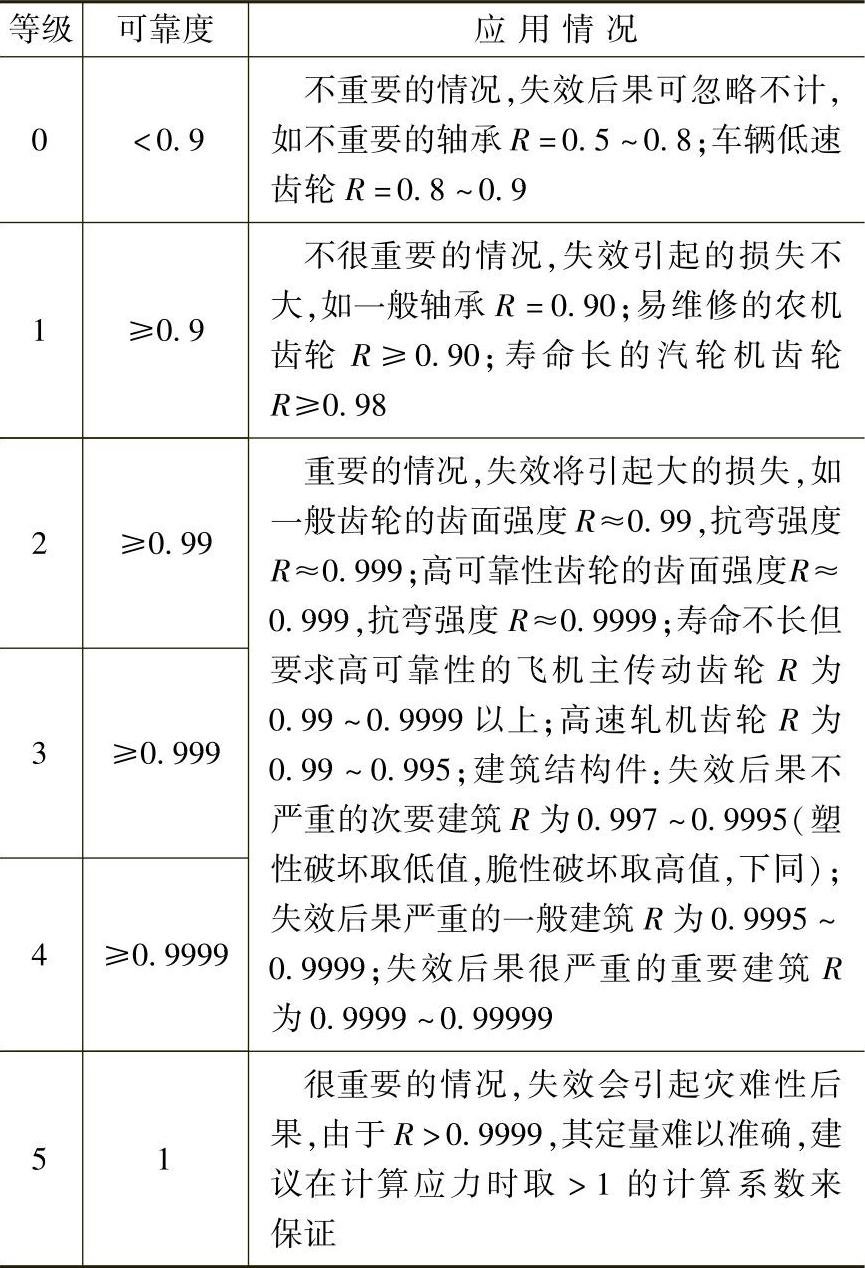
可靠度分类等级应用举例见表19-3。

3.可靠性设计程序及内容

制品的可靠性是由设计、生产、质量管理、维修、销售及用户等各环节人员共同工作而实现的，其中设计是主要环节。

传统机械零件设计采用确定性的材料性能参数、工作许用应力和安全系数，不考虑参数的分散性，而可靠性设计（或称概率设计）则把设计指标及有关参数作为随机变量处理，在给定的载荷条件下，应用统计与概率分析法设计出安全合理的零件或结构。可靠性设计的基本特点是将应力和强度作为随机变量处理，应用概率和统计方法进行分析、计算，定量地评价产品的失效率和可靠度。

表19-3 可靠度分类等级应用举例

以结构件强度的可靠性设计为例，其可靠性设计的基本程序如下：

1）确定制品可靠性定量指标和定性要求，以此作为设计、分析、制造、试验和验收的依据。

2）确定决定制品性能可靠性的设计变量，如选择制品用材料的强度、负载、尺寸等参数作为随机变量。变量一般均服从正态分布规律分布。

3）确定失效模式，如制品受拉应力断裂破坏或受疲劳失效破坏，根据确定模式可按照正态分布规律进行应力-强度分析，如图19-13所示。

由图19-13可知，当制品工作一段时间后，虽然工作应力平均值_μs仍小于制品强度平均值μ_δ，但由于参数的分散性，在两曲线干涉的阴影部分会出现工作应力超过制品强度，致使发生故障或失效，故当应力大于强度的全部概率即为失效概率，即发生不可靠现象，由此利用正态分布随机变量的代数运算公式计算出应力和强度的均值（μ_δ、μ_s）和标准差（δ_δ、S_s）。当均值为定值时，标准差值越小，则分散度越小，可靠性越高。当标准差值一定时，μ_δ与μ_s差值越大，则可靠性也越高，且可将均值和标准差值代入可靠性设计的计算公式中，直接计算出制品的可靠性，或设计规定可靠度的制品等各种计算，从而提高产品的可靠性。这种方法统称为可靠性设计方法。

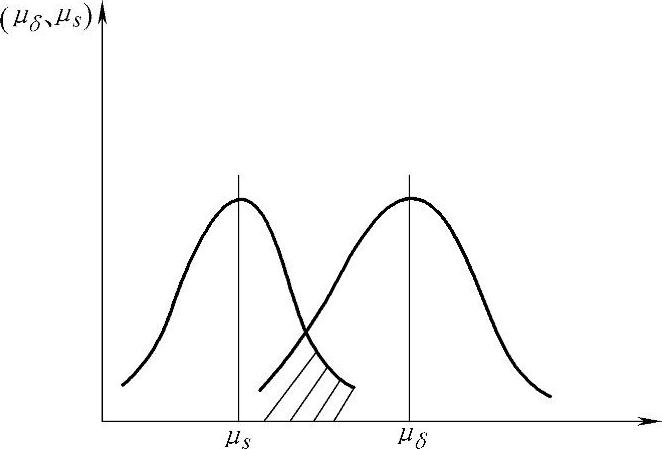
图19-13 应力-强度干涉模型（应力-强度分布曲线）

4.可靠性指标计算方法

可靠性设计可以以系统为对象，也可以部件、零件为对象。可靠性的目标也可以是各种性能（功能）、能源消耗、动力性能、安全性、维修性等各种指标，因此计算方法及采用的计算原理和公式也很多，仅机械零件的计算方法就有应力-强度干涉模型法、数值积分法、图解法、极限状态方程验算点法、索特卡洛模拟法、可靠度置信度和置信区间计算等。

但是，所有的可靠性设计及计算得到的结果都是理论值，且需各环节配合实际情况，通常采用一系列的可靠性试验来确认，试制新产品很少一次就成功。通常需经多次改进设计，逐步提高以达到可靠性目标值。在初步设计和技术设计告一段落，还需再进行可靠性预计，进行必要的可靠性试验，对重要的部分用故障模式、效应及危害度分析（FMECA）、故障树分析（FTA）等方法进行可靠性、安全性分析，邀请有关各方面人员专家就可靠性进行评议审查。将设计的缺陷、潜在的故障原因、弥补的对策反馈给设计人员，进行改进设计，逐步完成可靠性设计。